(1)平面の決定
平面とは…どの方向にも限りなく広がっている平らな面
例)2点A,Bを含む平面
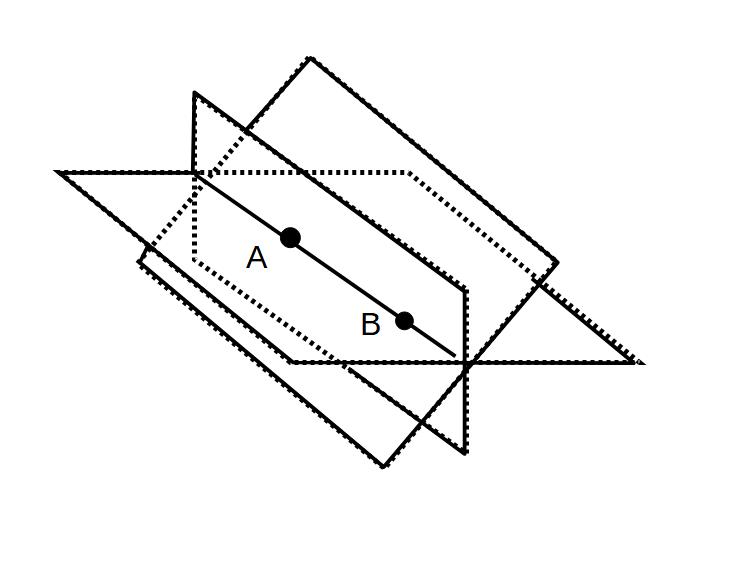
A,Bを含む平面は
いくつも作成できる
(A,Bを軸に面を回転すればたくさんできる)
では、2点AとBに、さらに点Cを含む平面ではどうなるでしょう。
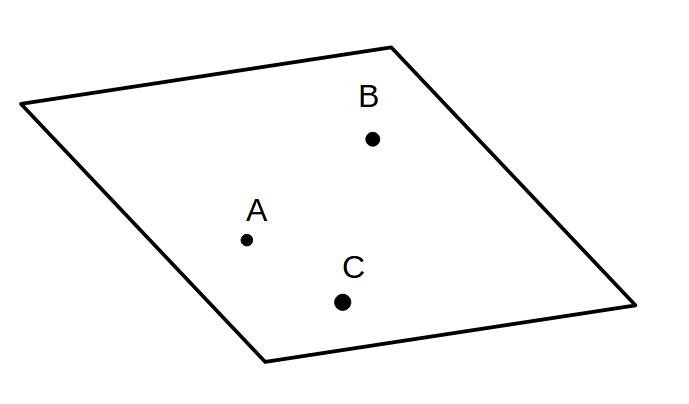
点が3点になると…
面は1つしかできない!
※点A,B,Cは一直線上にはない
さらに、この3点の関係は…
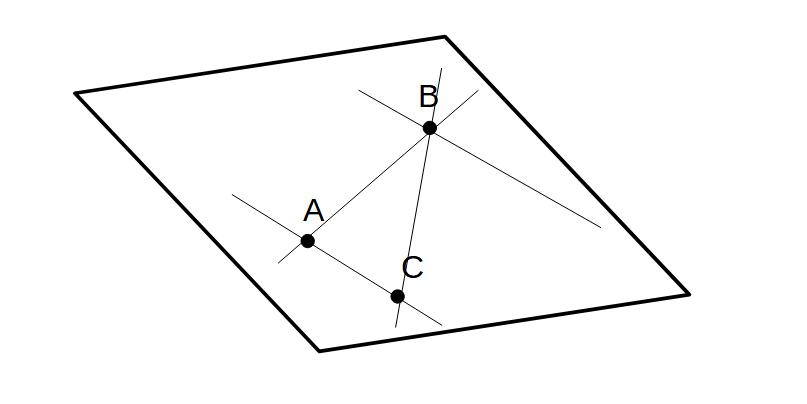
①2本の交わる直線を作れる
②2本の平行線を作れる
※平面の決定
①同一直線にない3点
②1つの直線とその直線上にない1点
③交わる2直線
④平行な2直線
このいずれか1つを満たせば、平面が1つに定まる
(2)直線と平面の位置関係
例)立方体の上の部分を切り取った図形で考えます。
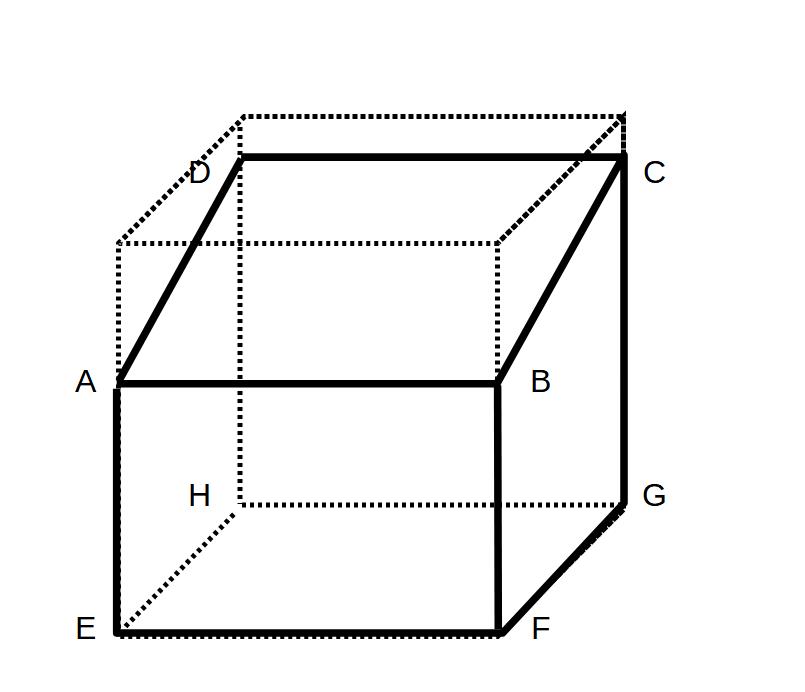
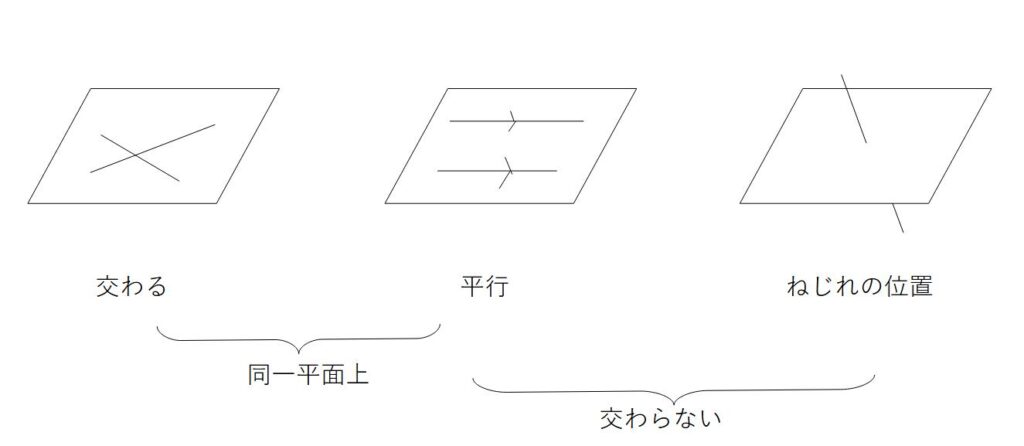
①直線と直線の関係
例1)直線BCと直線BF→交わっている
この直線同士は実際に触れあっている状態にあるので、交わっているということになります。
例2)直線BFと直線CG→平行
この直線同士は、触れ合っていない状態で、なおかつ立方体の辺同士で同じ方向に走っているので、平行であるといえます。
例3)直線BCと直線HG→平行ではなく、交わらない
=同一平面上になく、交わらない
=「ねじれの位置」にある
この直線同士は、交わらないかつ平行でもない状態です。これをねじれの位置といいます。
※直線と直線の位置関係
①交わる
②交わらない→同一平面上にある=平行
→同一平面上にない=ねじれの位置
例)の直線BCとFG
→それぞれを延長すれば交わる
=この2本の直線は交わっている!
②直線と平面の関係
例)平面ABCDとの関係
例1)直線AB→平面ABCD上にある(平面ABCDに含まれる)
例2)直線BF→平面ABCDと交わっている
例3)直線HG→平面ABCDとは交わらない=平行
※直線と平面の位置関係
①直線が平面上にある
②直線と平面が交わる(交わる点を交点「こうてん」という)
③直線と平面が交わらない=平行
この3つのいずれかになる
③平面に垂直な直線
例)平面EFGHと直線AE
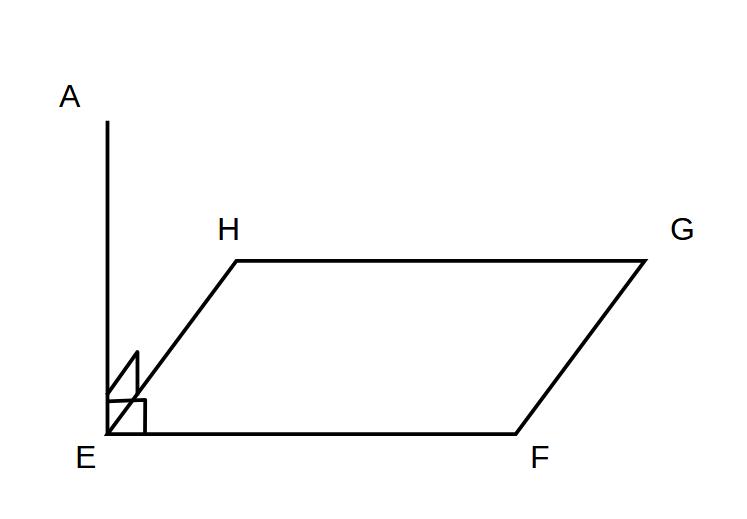
AEはAE⊥EF
AE⊥EH
のいずれも満たす
→平面EFGHと直線AEは垂直である。
※線分AEの長さを
「点Aと平面EFGHの距離」という
※①ある直線が平面と交わり、その交点を通るすべての平面上の直線と垂直になるときその直線は平面に垂直であるという。
②(実際には)平面に交わる直線はその交点を通る平面上の2直線に垂直ならbば、その平面とも垂直となる。
④平面と平面の位置関係
例1)(上の立方体を切ったやつに戻って)面ADHEと面BCGF→交わらない=平行
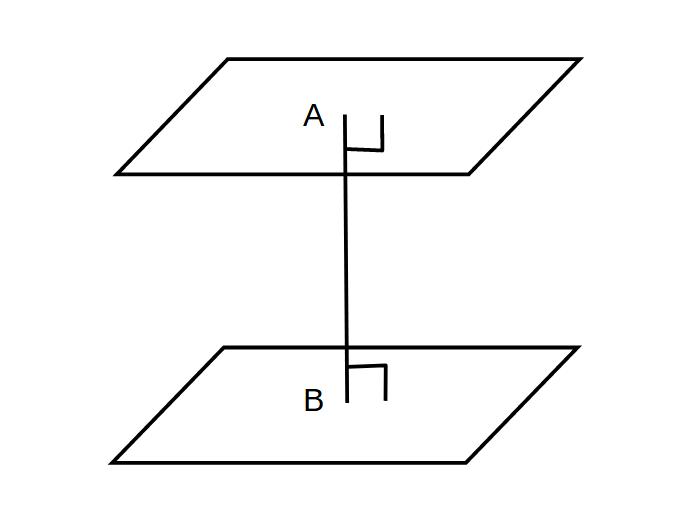
※平行な2平面の距離
平行な2平面の両方に垂直な線分ABの長さ
=2平面の距離
上の立方体を切った図形でいうと、
面ADHE//面BCGF
AB、CD、EF、GHは両平面に垂直な線分である
例2)面ABCDと面ABFE→交わる
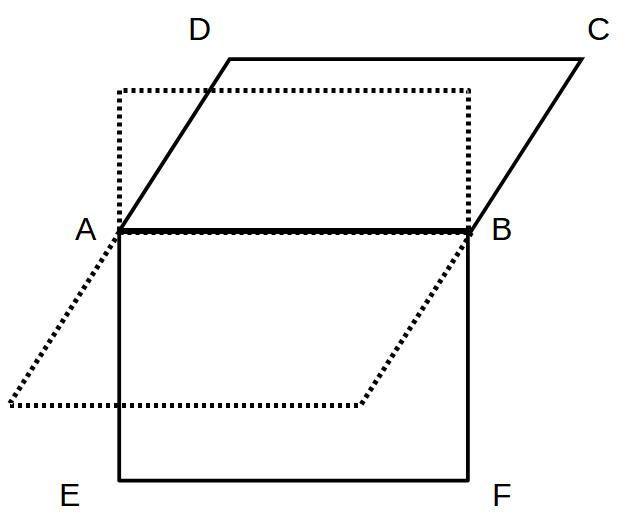
(上の立方体を切ったやつに戻って)
平面と平面の交わりには直線ができる
=交線(ABが交線)
1.平面→限りなく広がっていく
→交わっているように見えなくても、辺面を広げていけば交わるものがある
→面ABCDと面EFGH
2.垂直に交わる
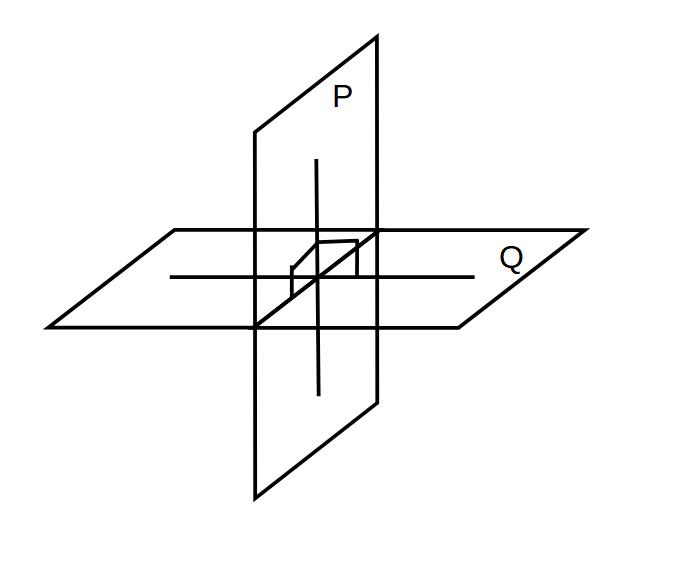
平面Pが平面Qに垂直な直線を含むとき
平面Pは平面Qに垂直である
(上の立方体を切ったやつに戻って)
平面EFGHに垂直な面
→平面ABFE、平面BFGC、平面CDHG、平面ADHE