〇立体の切り口
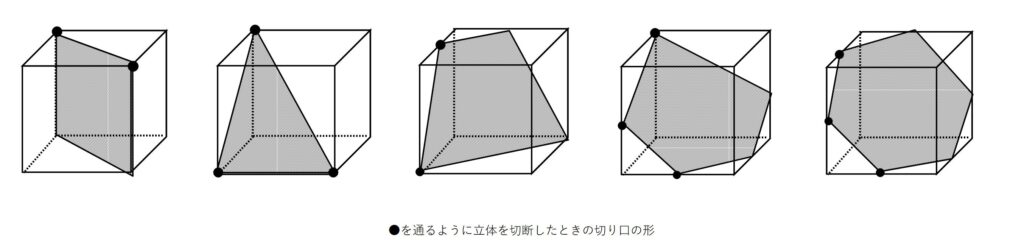
→立体を平面で切るときの切り口。
※主に立方体・直方体を切断し、その断面について勉強します。
まず、切り口の線が書けるようになりましょう。
考え方
①2つの平面の交わりは直線(交線)
②3つの平面が交わってできる3直線は平行になるか、1点で交わる
③平行な2平面に他の平面が交わるときその2つの交線は平行である
書き方
①同一平面上の2点は結ぶ
②平行な面の切り口の線は平行
③面を延長して考える
〇最短距離
・立体の表目を通るときの最短
・立体にひもをかけるときの最短
→展開図にして直線になる=2点間の最短経路は直線
例)A~Gまでの最短距離を展開図に記入せよ。
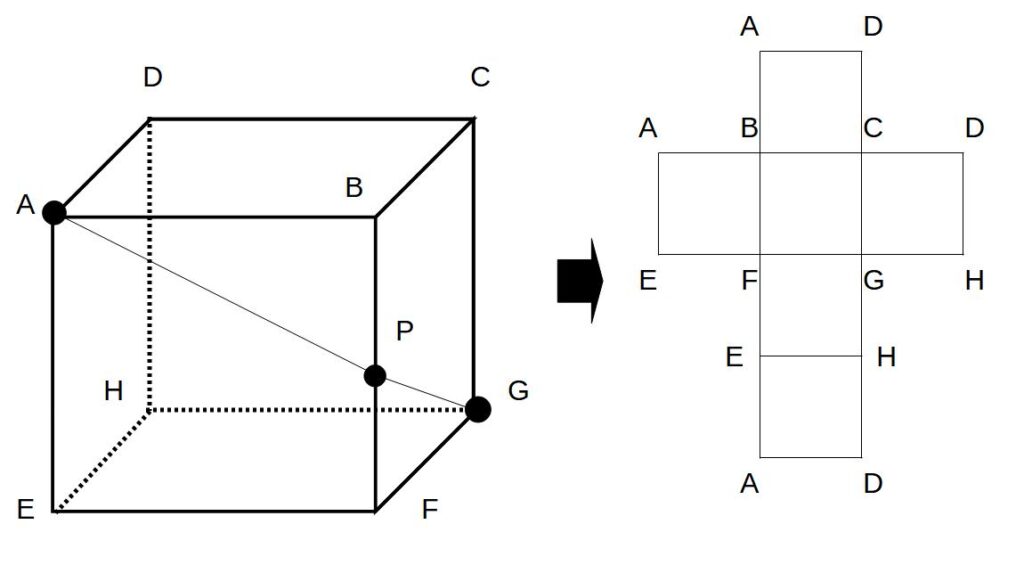
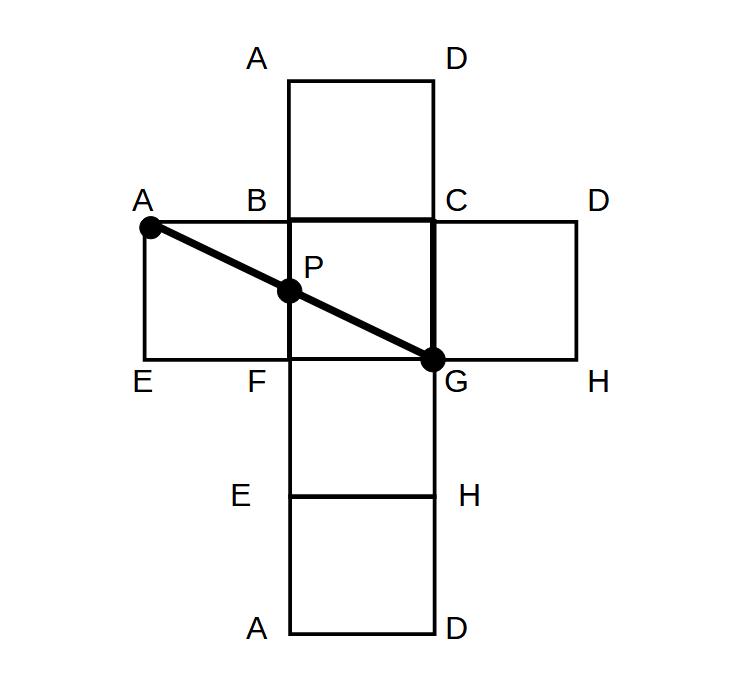
最短距離は直線になるので、
点Aから点Gまでの直線を引けばよい
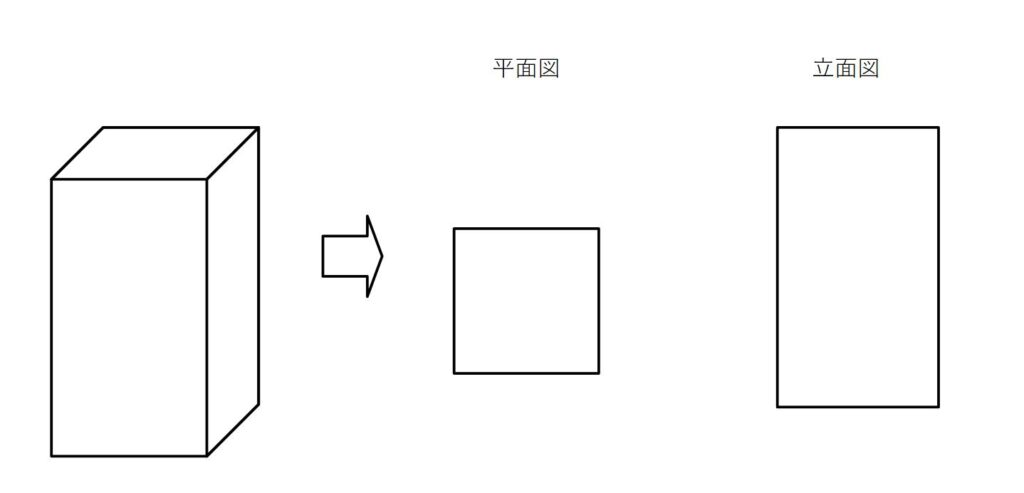
〇投影図
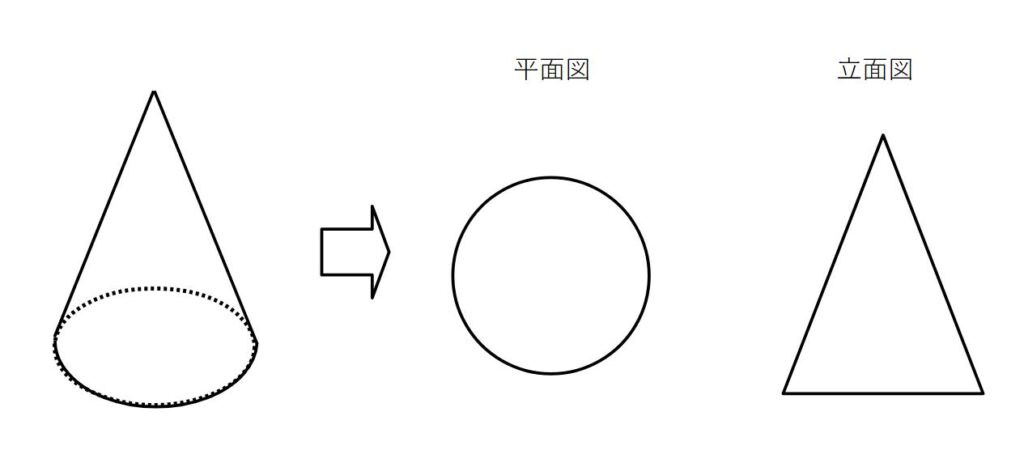
投影図とは…立体を1つの方向から見て平面に表した図のこと
真上から見た図…平面図
正面から見た図…立面図という
〇切断立体の体積
例)
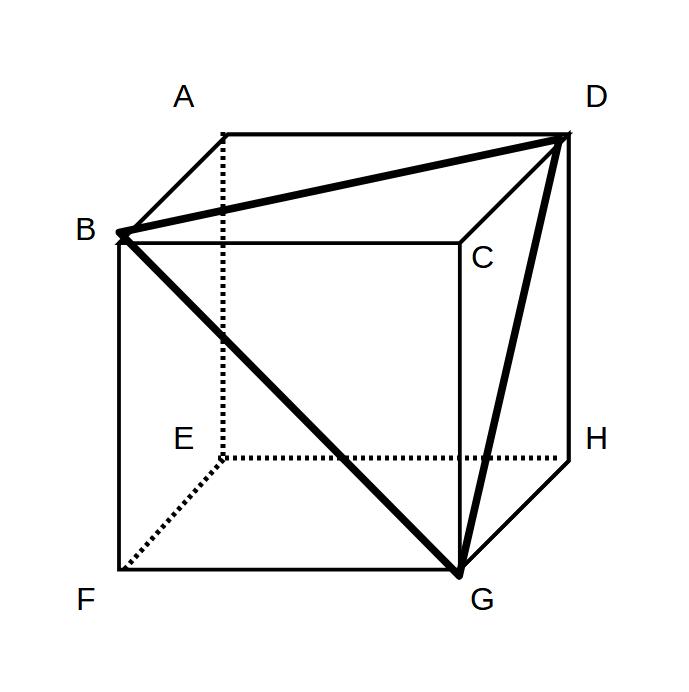
一辺6cmの立方体ABCD-EFGH
3点B,D,Gを通る平面で
切ったときにできる2つの立体の
体積をそれぞれ求めよ
まず、切断されてできた形がどのような形であるかを考える
→切断すると、Cを含む方の立体は…三角錐
→三角錐D-BCGとみる!
三角形の1辺および高さはすべて6㎝なので、
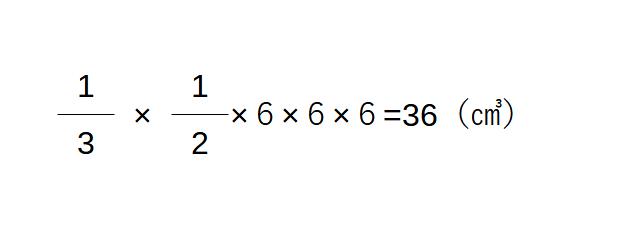
Cを含まない方の立体は、立方体の体積から先ほど求めた三角錐の体積をひけばよいから、
6×6×6-36=180(㎤)
となる。
例)
図のような円すいを切り取った立体がある。
この実践部分の立体(プリンの型みたいなやつ)
の体積を求めよ。
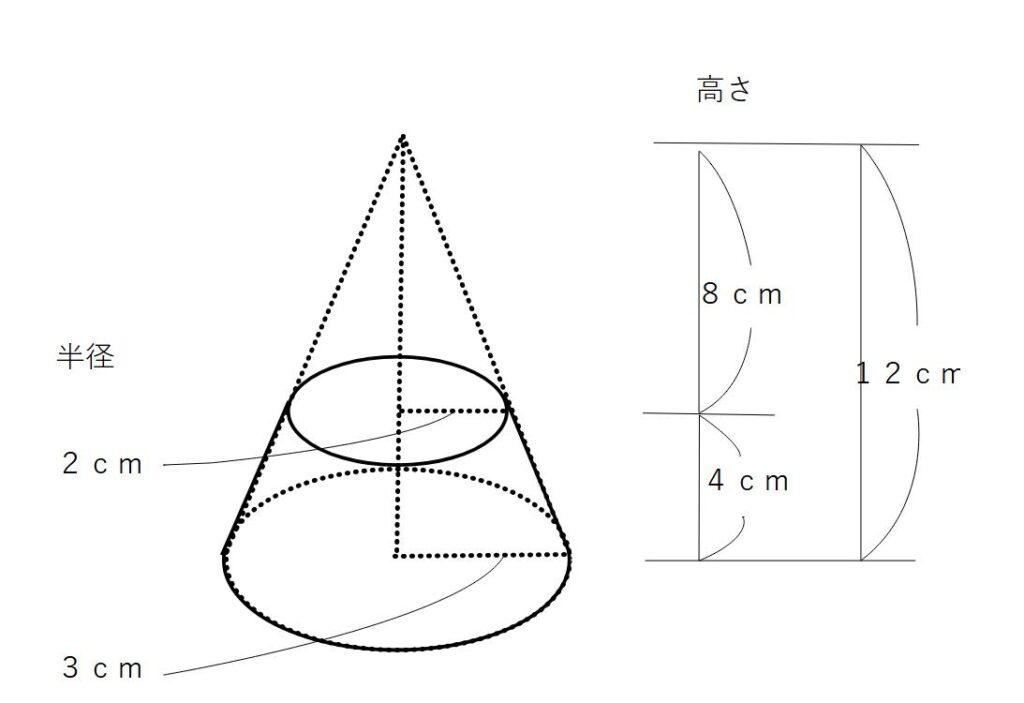
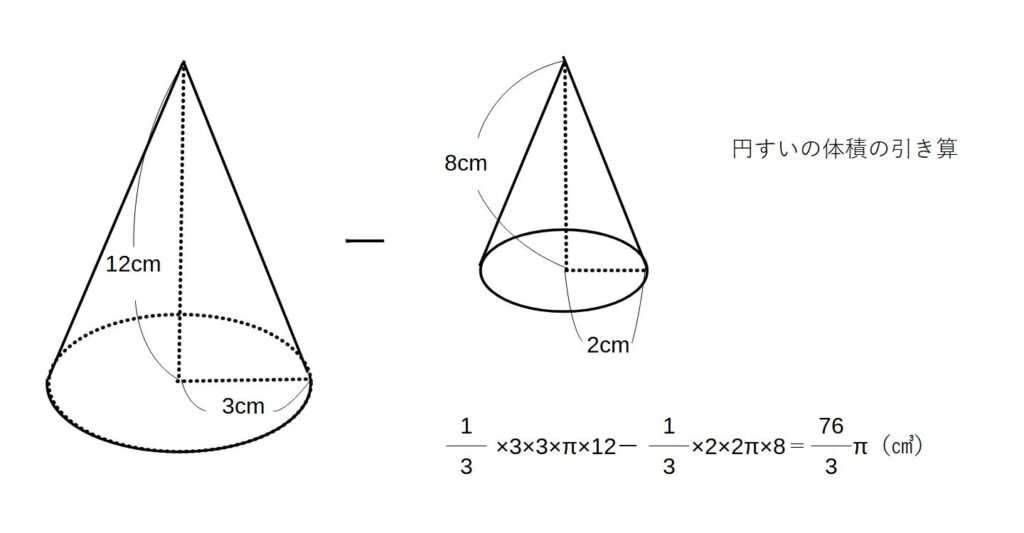
解き方)
①半径3㎝の円すいの体積を求める
②半径2㎝の円すいの体積を求める
③①の体積から②の体積を引く
〇球の体積・表面積
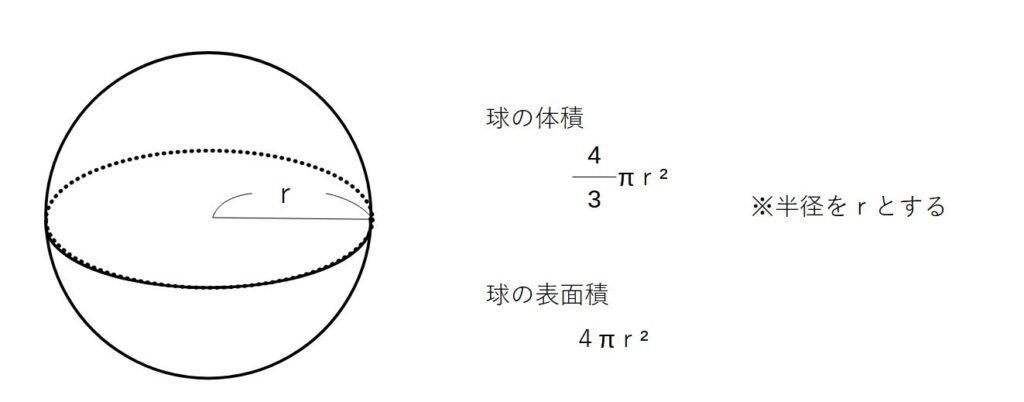
この場合、球の体積は「身の上に心配ある惨状」
球の表面積は「心配ある事情」とゴロで覚えましょう。