〇平面図形(三角形・平行四辺形など)の面積や空間図形(円柱・三角錐など)の体積・表面積などを、文字を使って表す
→文字の含まれているまま、割合などを計算で求める
例1)ある三角形の底辺と高さをそれぞれ2倍にした時、面積をもとの三角形の何倍になるか
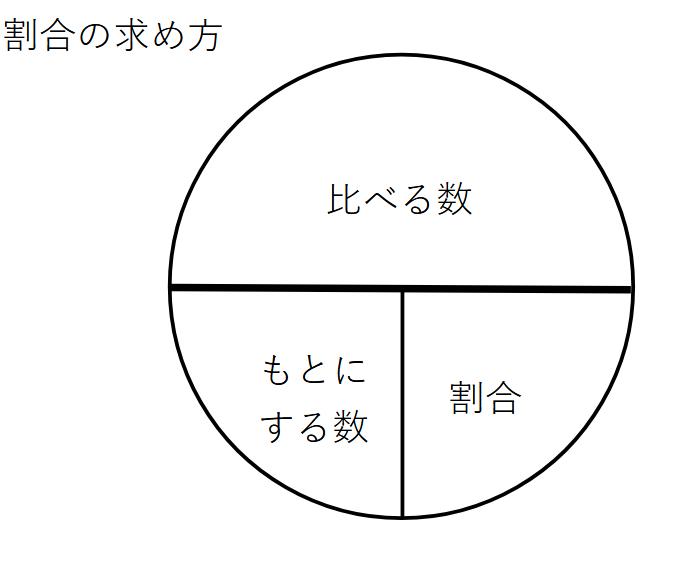
※「何倍になるか」→割合を求める!
割合を求める式が必要
①底辺の長さをa、高さをhとして、元の三角形の面積を文字式で表す
元の三角形の面積 \( \displaystyle \frac{1}{2}ah \)
②底辺a、高さhをそれぞれ2倍すると、2a、2h
→これを使ってくらべる三角形の面積を文字式で表す
くらべる三角形の面積
\( \displaystyle \frac{1}{2} \times 2a \times 2h=2ah \)
③文字が含まれているままでよいから、割合を計算してみる
(くらべる三角形の面積)÷(もとの三角形の面積)
\( \displaystyle 2ah \div \frac{1}{2}ah \)
\( \displaystyle 2ah \times \frac{2}{ah} \)
\(=4\) すなわち4倍
例2)ある円すいの底面の半径を2倍、高さを3倍にすると、もとの円すいの体積の何倍になるか
①底面の半径の長さをr、高さをhとすると、
元の円すいの体積は→
\( \displaystyle \frac{1}{3}\pi r^2 h \)
となる
②底面の半径を2倍にすると2r、高さを3倍にすると3hと表せるから、比べる円すいの体積は→
\( \displaystyle \frac{1}{3} \times \pi \times (2r)^2 \times 3h \)
\( =4 \pi r^2 h \)
③したがって、→のようになる
\( \displaystyle 4 \pi r^2h \div \frac{1}{3} \pi r^2 h=12 \)
すなわち12倍
式を解くことはできても、問題文を見て式を作るのはなかなか難しいかと思います。
しかし、パターンは存在しますので、限られたパターンをたくさんこなすことで身に着けることができます。
頑張りましょう。