今回は連立方程式の応用、文章題などへの対応を勉強します。
まずは、1年次でもやっていますが、文章題の解き方のおさらいです。

これをふまえたうえで、実際に問題を見ていきましょう。
(1)個数と代金
ここでは、まず2パターン見ていきます。
例1)
1個200円のリンゴと1個40円のミカンを合わせて26個買ったら1840円になった。リンゴ、ミカンをそれぞれ何個買った?
手順1)
わからないもの(求めたいもの)を、文字でおく
リンゴの数→x個
ミカンの数→y個
とおく。
手順2)
文章の中から数量関係等に注目し、文字で表現できるのはないか?
それを「=」で結ぶ
①リンゴとミカン合わせて26個
→ x+y=26
②120円のリンゴをx個買った→120x円
40円のミカンをy個買った→40y円
→全部で1840円になった
12x+40y=1840
手順3)
「=」で結べたので方程式は完成!
あとは計算
\( \begin{cases}x+y=26…①\\
\\
140x+40y=1840…②
\end{cases}
\)
①×4ー②÷10
\(\begin{array}{rr}
& 4x+4y=104\\
-\big{)}&12x+4y=184\\
\hline
&-8x=-80\\
&x=10
\end{array}
\)
これで、式を作り、連立方程式をときます。
x=10なので、①に代入して
10+y=26
y=16
よって x=10,y=16
∴リンゴ10個ミカン16個
※ちなみに、この問題では1次方程式でも解答が可能です。
リンゴをx、ミカンを(26-x)として、
120x+40(26-x)=1840
x=10
とも可能です。
ただ、おそらく定期テストなどでは、問題文に「連立方程式を使って解きなさい」的な文言が入っている可能性があり、ここでは素直に連立方程式で解答しましょう。なんでも1次方程式で解く、なんでも連立方程式で解く、ではなく、どちらでも臨機応変に対応できるようになりましょう。
例2)
ノーツ2冊とエンピツ3本買うと510円、ノート1冊とエンピツ2本買うと300円になる。ノート1冊とエンピツ1本の値段は?
手順1)
ノート1冊x円
エンピツ1本y円
手順2)
①1さつx円のノート2冊買う→2x円
1本y円の鉛筆を3本買う→3y円
合計が510円→2x+3y=510
②1冊x円のノート1冊買う→x円
1本y円の鉛筆を2本買う→2y円
合計が300円→x+2y=300
手順3)
\( \begin{cases}2x+3y=510…①\\
\\
x+2y=300…②
\end{cases}
\)
①ー②×2
\(\begin{array}{rr}
& 2x+3y=510\\
-\big{)}&2x+4y=600\\
\hline
&-y=-90\\
&y=90
\end{array}
\)
y=90がわかったので、②に代入
x+180=300
x=120
x=120,y=90
よって、ノート1冊120円、エンピツ1本90円
(2)整数
次は整数の問題です。ちょっと具体的なイメージがつかめないので難しいかもしれませんが、パターンさえ覚えてしまえば大丈夫です。
ここでも2パターン見ていきましょう。
例1)
大小2つの整数がある。大きい数と小さい数の和は120で、大きい数から小さい数を引いた差は40である。この整数は?
手順1)
大小の整数をあらかじめそれぞれx、yとおく(x>yと決めておく)
手順2)
①和が120→x+y=120
②差が40→x-y=40
手順3)
式が立てば解くだけです。
\( \begin{cases}x+y=120…①\\
\\
x-y=40…②
\end{cases}
\)
①+②
\(\begin{array}{rr}
& x+y=120\\
+\big{)}&x-y=40\\
\hline
&2x=160\\
&x=80
\end{array}
\)
x=80を①に代入
80+y=120
y=40
よって、80と40
※整数で表現される関係式
例)2つの整数x、yにおいて、xをyで割ると商は4で余りは3になる。
→x÷y=4…3
→x=4y+3 になる!
A÷B=C…Dのとき、A=B×C+D
例2)
2けたの正の整数がある。この整数の十の位の数と一の位の数の和は6で、十の位の数と一の位の数を入れ替えると元の数より18小さくなる。元の数は?

これを見ると、2桁の数→10a+bと表現できることがわかる!
手順1)
十の位→x
一の位→y
手順2)
元の数は10x+y
入れ替えた数は10y+x
手順3)
①十の位と一の位の和が6
→x+y=6
②入れ替えた数は元の数より18小さい
→(元の数)=(入れ替えた数)+18 または
(元の数)ー(入れ替えた数)=18
→(10x+y)ー(10y+x)=18
=9x-9y=18
手順4)
\( \begin{cases}x+y=6…①\\
\\
9x-9y=18…②
\end{cases}
\)
①×9+②
\(\begin{array}{rr}
& 9x+9y=54\\
+\big{)}&9x-9y=18\\
\hline
&18x=72\\
&x=4
\end{array}
\)
①に代入 \(y=2\)
よって元の数は42
※この②式は、9で割るとさらに計算が楽になります(x-y=2になる)
※こういった類の問題で、xとyが出てしまったら、そのまま安心してxとyの答えを回答欄に書いてしまうというミスをする人が必ずいます。絶対にもだいぶんで聞かれている答えで解答するようにしてください。(今回なら42,など)
(3)速さ
速さの計算のおさらいです。
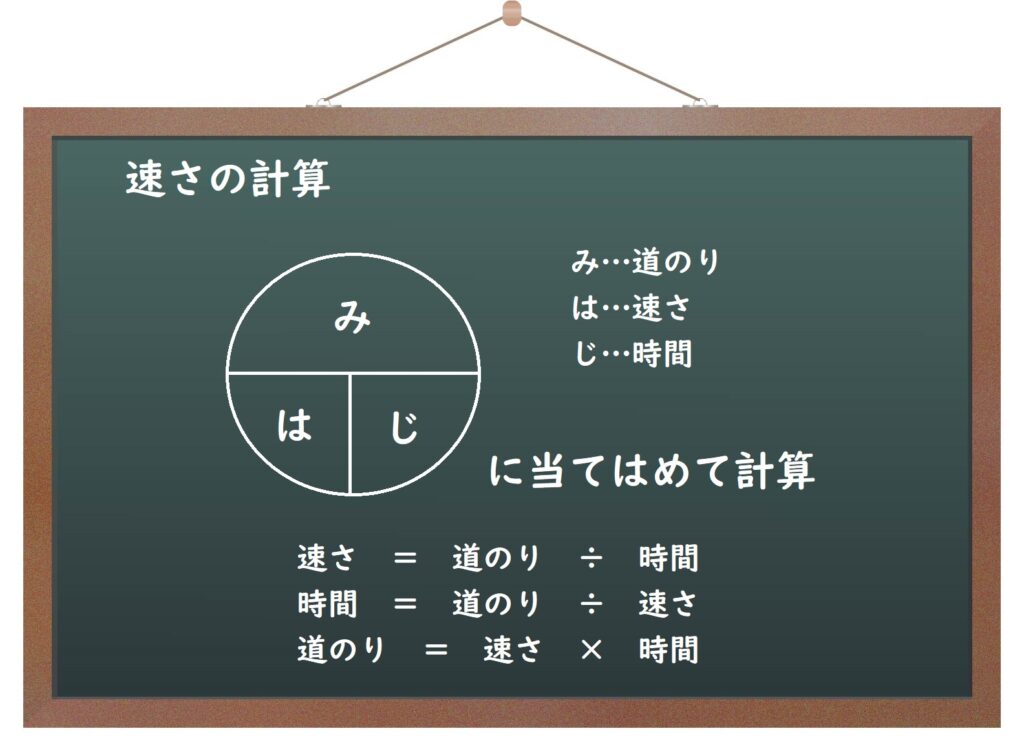
連立方程式になっても、この速さの公式を使って式を立てていきます。
例1)
A君は、家から学校までの1.9㎞の道のりを、はじめのxmは毎分70mの速さで歩き、その後のymは毎分150mの速さで走って、ちょうど18分で學校に着いた。xとyの値は?
手順1)
わからないものはすでにxyになっている
手順2)
速さの問題は、図に書き出してみましょう。
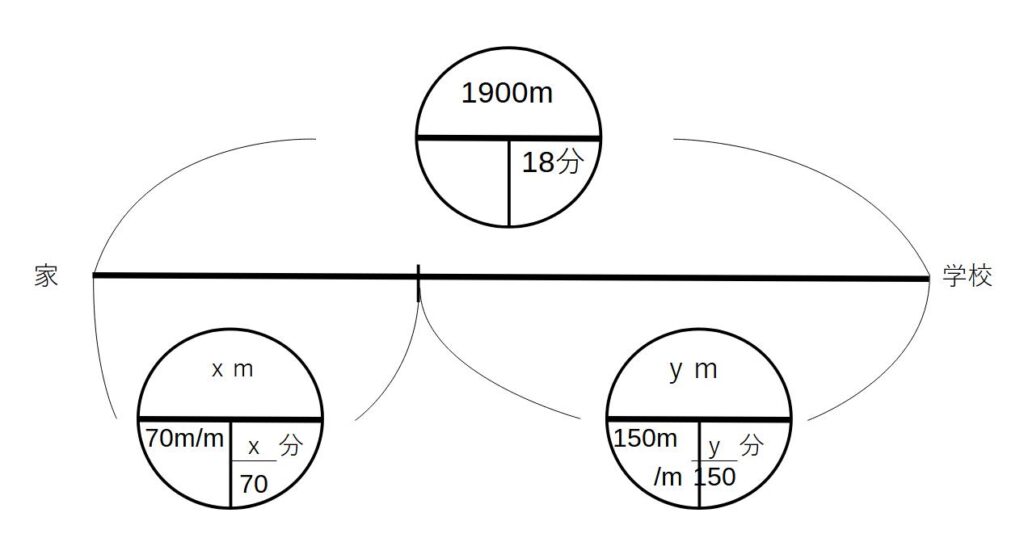
手順3)
対応する場所それぞれで等式が作られるところを探す
※速さは足し引き出来ないからダメ
\( \begin{cases}①道のり → 1900=x+y\\
\\
②時間 → 18=\displaystyle \frac{x}{70}+\frac{y}{150}
\end{cases}
\)
手順4)
先ほどの式を連立方程式として解く
計算すると、
x=700m、y=1200m
\( \begin{cases}x+y=1900…①\\
\\
\displaystyle \frac{x}{70}+\frac{y}{150}=18…②
\end{cases}
\)
つぎは、ちょっと難しくなります。
例2)
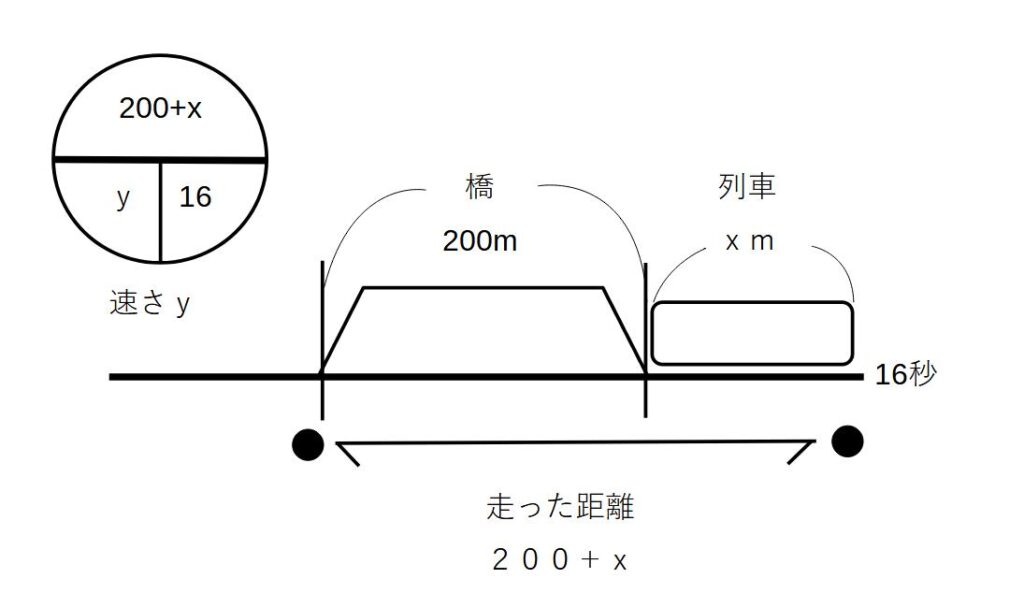
一定の速さで走っている列車が200mの鉄橋を渡り始めてから完全にわたり終わるまで16秒かかり、700mのトンネルに完全に隠れている時間が44秒であった。列車の長さと速さは?
手順1)
列車の長さをx、速さをyとする
手順2)
図に書き出してみます。
①鉄橋
移動距離が明確になるように、列車の先頭がどこまで動いたかを●をつかって書いています。
左上の〇にあるように式を立てると、
200+x=16×y
となります。
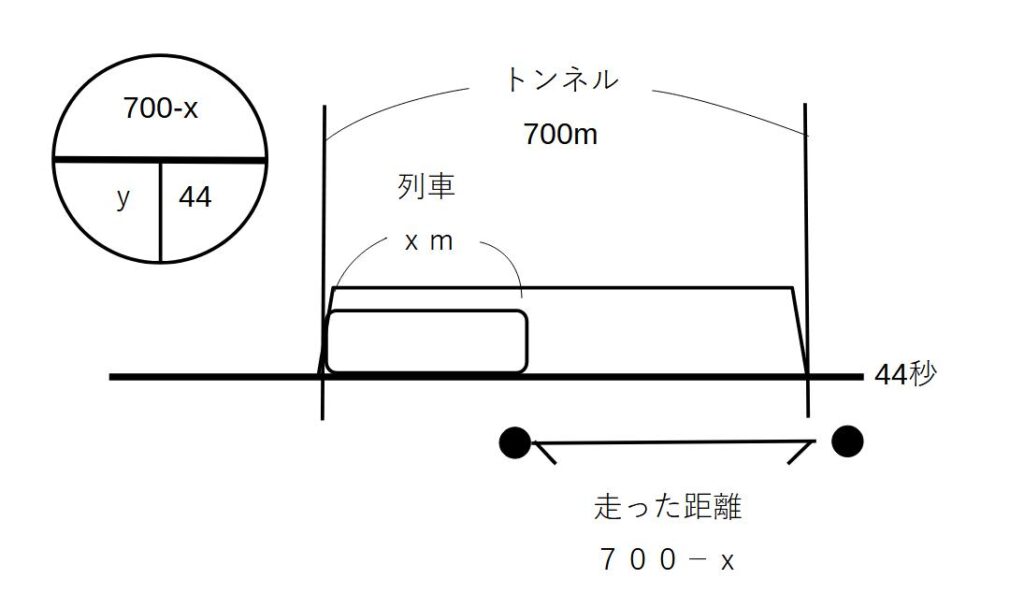
②トンネル
橋のときとおなじように、左上の〇の中にあるように式を立てます。
700-x=44×y
となります。
あとは、連立方程式を解いていきます。
\( \begin{cases}200+x=16y…①\\
\\
700-x=44y…②
\end{cases}
\)
①+②
\(\begin{array}{rr}
& 200+x=16y\\
+\big{)}&700-x=44y\\
\hline
&-60y=-900\\
&y=15\\
&x=40
\end{array}
\)
よって、列車の長さ40m、速さ15m/秒
例3)
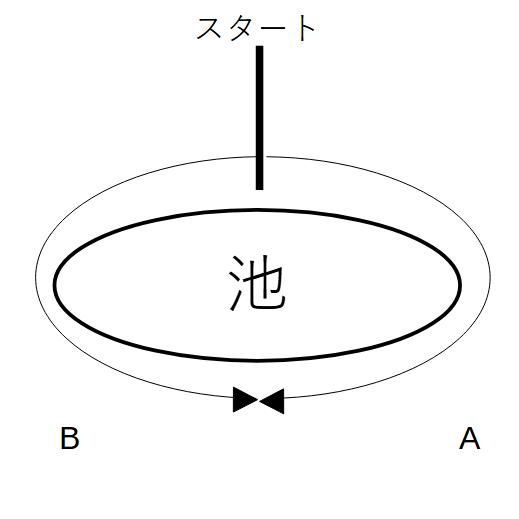
1周800mの池の周りをAtoB2人がまわるとき、同時に同じ方向に出発すると30分後にAがBに追いつき、反対方向に出発すると5分後に2人は出会う。2人の速さは?
手順1)
Aの速さ…x、Bの速さ…yとする
手順2)
①同じ方向に出発した場合
Aの進んだ距離=B+1周
30x=30y+1800
※時間×速さの差=1周分
30(x-y)=1800

②反対方向に出発した場合
Aの進んだ距離+Bの進んだ距離=1周
5x+5y=1800
※時間×速さの和=1周分
5(x+y)=1800
\begin{cases}30x=30y+1800…①\\
\\
5x+5y=1800…② \end{cases}
すると、このような連立方程式が組めます。
あとは、計算していくだけです。
②×6 30x+30y=10800…②’
①+②’
30x-30y=1800
30x+30y=10800
60x=12600
x=210
②に代入
1050+5y=1800
5y=750
y=150
よって、A…210m/分、B…150m/分
(4)割合
割合の表現方法、おさらいです。

具体例をちょっと練習しておきましょう。
例)
①1000の10%は?
②200の2割は?
③1500円の15%増しは?
④2000円の20%引きは?
⑤1000円の4割増しは?
⑥2000円の3割引きは?
例解)
①\( \displaystyle 1000 \times \frac{10}{100} =100 \)
②\( \displaystyle 200 \times \frac{2}{10} =40 \)
③\( \displaystyle 1500+1500 \times \frac{15}{100}=1500 \times (1+ \frac{15}{100}) =1725 \)円
④\( \displaystyle 2000-2000 \times \frac{20}{100} =2000 \times (1- \frac{20}{100})=1600 \)円
⑤\( \displaystyle 1000+1000 \times \frac{4}{10} =1000 \times (1+ \frac{4}{10})=1400 \)円
⑥\( \displaystyle 2000-2000 \times \frac{3}{10} =2000 \times (1- \frac{3}{10})=1400 \)円
これさえできれば、あとは等式を作れば計算するのみです。
→表などを書いてみると、さらにわかりやすいです。
2パターン見ていきましょう。
例1)
昨年は商品A、Bの代金の合計が1300円だったが、今年はAが10%値上がりし、Bが20%値上がりしたため、商品A、Bの代金の合計が1510円になった。今年の商品A、Bの代金は?
手順1)
今年の代金A→x、B→yとしたい。
しかし、問題文では、「昨年は商品A、Bの代金の合計が1300円だった」とあり、基準が昨年の金額になっている!
→昨年の代金A→x、B→yとおく
手順2)
表を作成してみる
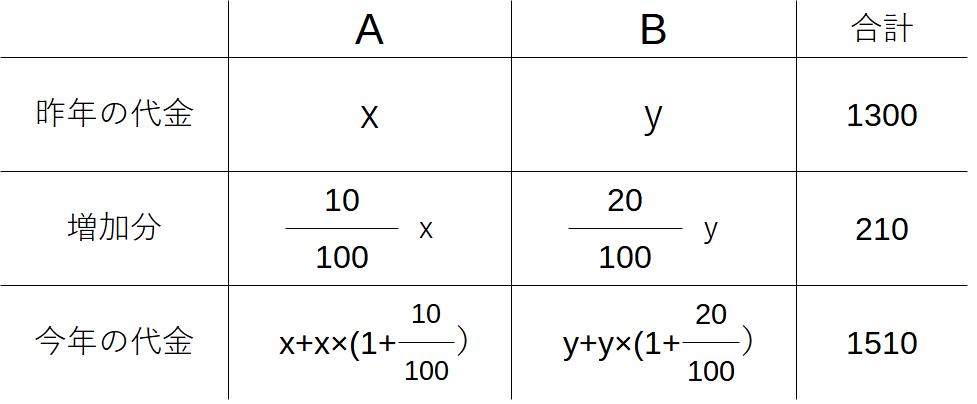
この表を使って、式を作ってみる。
※増加分、今年の代金については、少数で表現せず、分数で書くようにしましょう。小学校では少数で割合を表現していたため、なかなか慣れないかもしれませんが、たくさん問題を解いて慣れていきましょう。
手順3)
表をもとに式を作る
※ちなみに今回は②式が今年の代金ですが、増加分で②式を作ってもOKです。
\begin{cases}x+y=1300…①\\
\\
\displaystyle \frac{110}{100}x+ \frac{120}{100}y=1510…② \end{cases}
手順4)
連立方程式を解いて、x=500、y=800となる。
でも、これで終わりではない!
これで求めた数は、「昨年の代金」であることをわすれないように!
今年の代金は、「Aは10%値上がり」→1.1xとなり、1.1×500=550
「Bは20%値上がり」→1.2yとなり、1.2×800=960
よって、A=550円、B=960円となる。
例2)
ある中学校の生徒数は、昨年度が男女合わせて930人だった。今年度は男子が5%減、女子が8%減で合計870人だった。
今年度の男子・女子の生徒数は?
手順1)
昨年度の男子→x人、昨年度の女子→y人とおく
手順2)
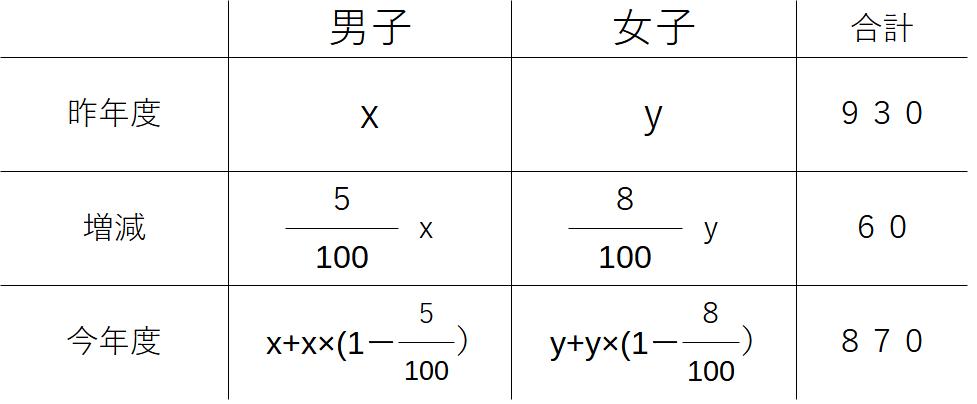
全問と同様、表を作成して、整理してみる。
このまま、式の作成が可能となる。
手順3)
式に起こします。
先ほどと同様、②式は今年度ではなく、増減を2式に充ててもOKです。
\begin{cases}x+y=930…①\\
\\
\displaystyle \frac{95}{100}x+\frac{92}{100}y=870…② \end{cases}
※②は、\(\displaystyle \frac{5}{100}x+\frac{8}{100}y=60\)でも可
手順4)
連立方程式を解いて、x=480,y=450となります。
手順5)
こちらも昨年度の数値なので、あくまで問われているのは「今年度」ですから、今年度の数値に直します。
男子→480×95/100=456
女子→450×92/100=414
よって、男子456人、女子414人 となります。
(5)濃度
こちらもおさらいしておきます。
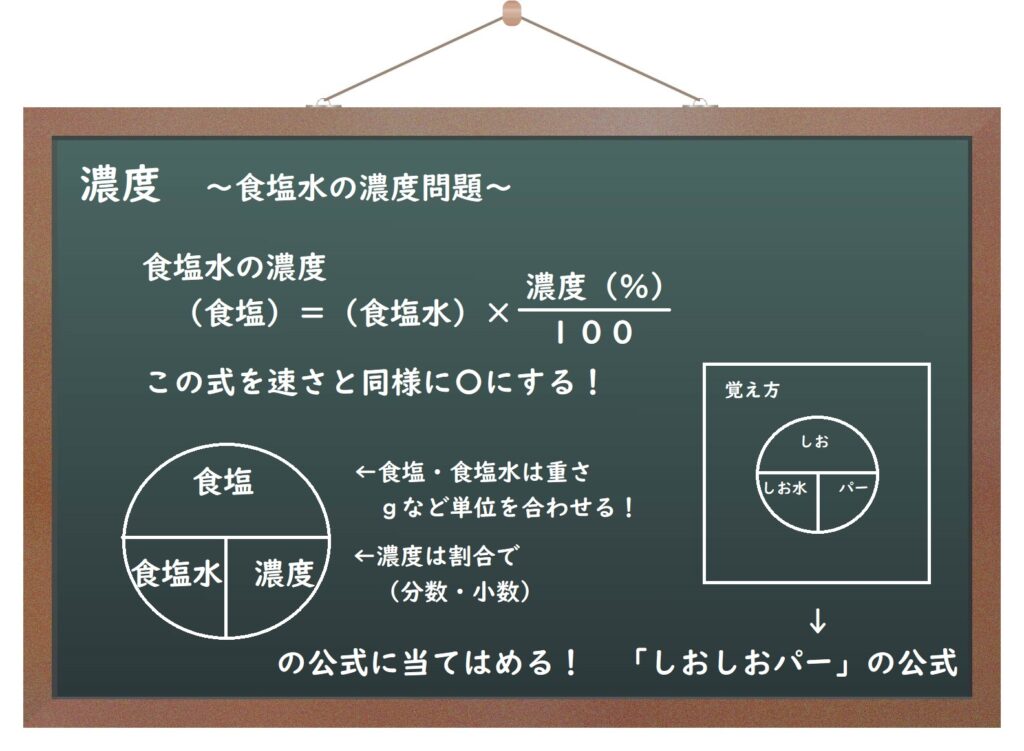
この形に当てはめてしまえば、濃度の問題は解答できます。
例)
10%の食塩水と5%の食塩水を混ぜて、8%の食塩水を450gつくりたい。2種類の食塩水をそれぞれ何gずつ混ぜればよい?
手順1)
10%の食塩水→xg
5%の食塩水→yg とおく
手順2)
図に当てはめる
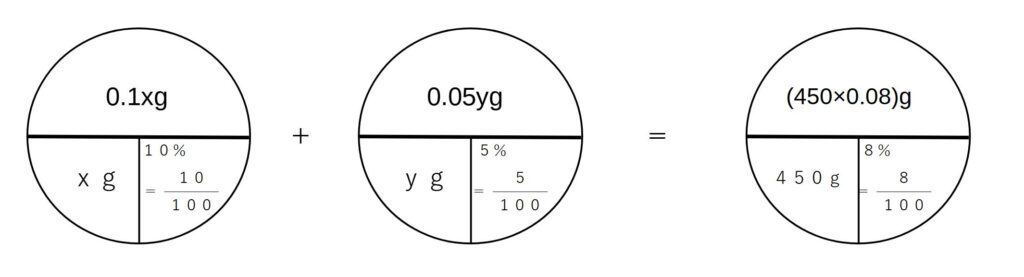
手順3)
上の図より、等式を2つ作る
割合で式を作らないように!
(足し引きができないから)
\begin{cases}0.1x+0.05y=450\times0.08=36…①\\
\\
x+y=450…② \end{cases}
手順4)
連立方程式を解いていきます。
これを解いて、x=270,y=180
よって、10%食塩水 270g
5%食塩水 180g となります。
\begin{cases}0.1x+0.05y=36…①\\
\\
x+y=450…②
\end{cases}