1次関数のグラフ
まず、1年生で習った比例のグラフを思い出してみましょう。
例)y=3xのグラフを書け
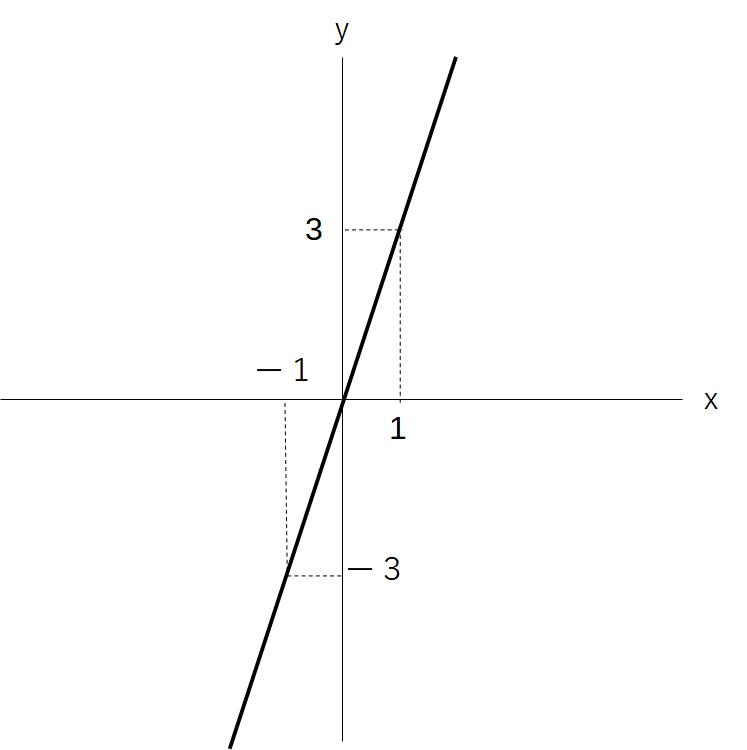
図のような直線のグラフができます。
y=3xなので、xが1増えると、yが3増える、という関係のグラフができるはずです。
1年生の復習なので、一度書いてみるといいでしょう。
では、続いて、こういった式のグラフはどうなるでしょうか。
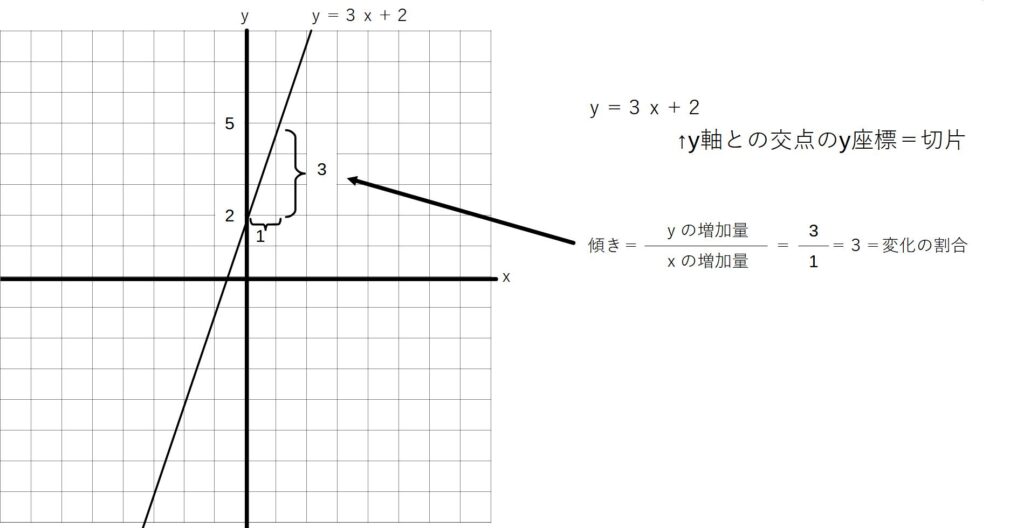
例)y=3x+2のグラフを書け
こんどは新たに+2がついています。
まず実際に、どういった数値になるのか、表で書き表してみます。
実際に式の中のxにそれぞれの数値を代入して計算すると、表のようになります。これを、グラフに点を取ってみます。
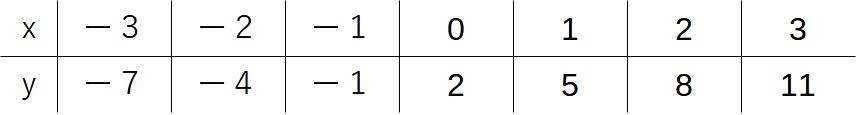
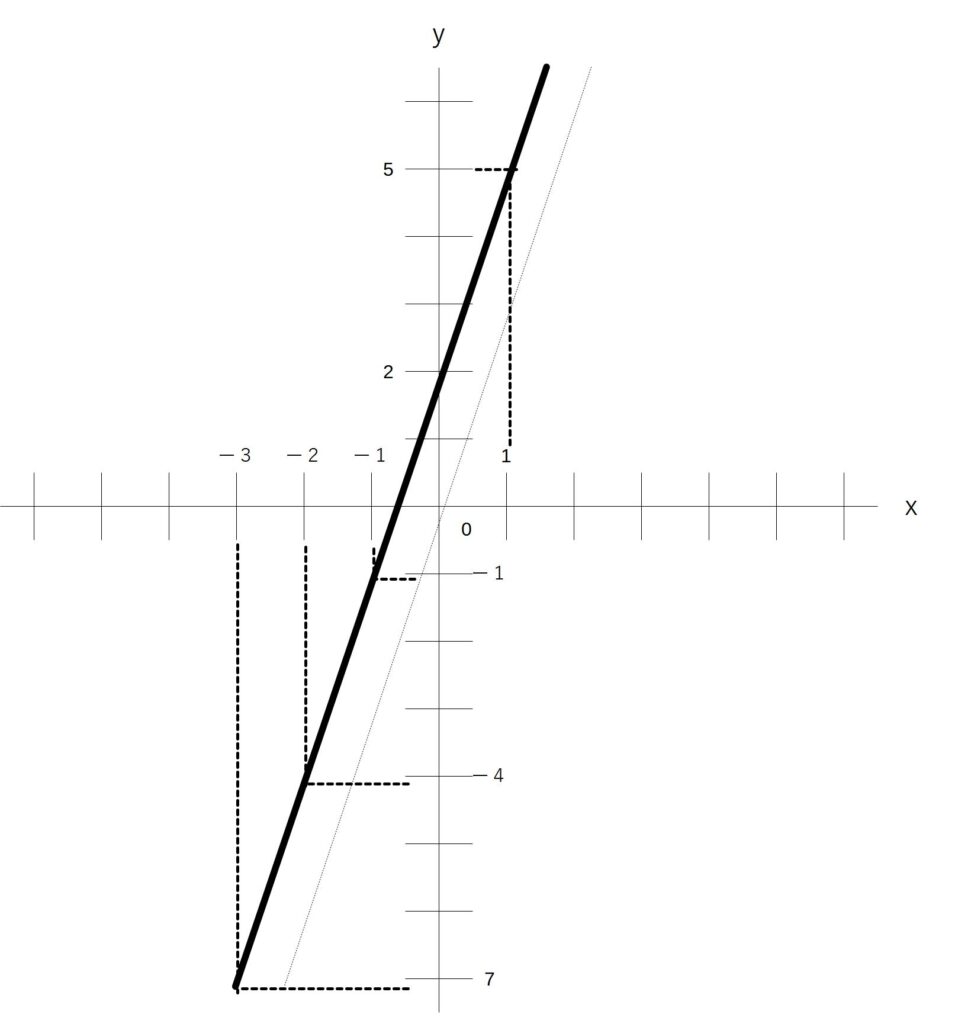
実際にグラフを書いてみました。
太線がy=3x+2のグラフです。
原点(0,0)を通っている細線のグラフはy=3xのグラフです。
こうしてみると、y=3x+2のグラフとは、y=3xのグラフをy軸に+2だけ平行移動させています。
つまり、y=ax+bのグラフのbの部分は、y軸方向に平行移動した形であるといえます。
似たようなのをもう一つ見てみましょう。
例)y=3xー1
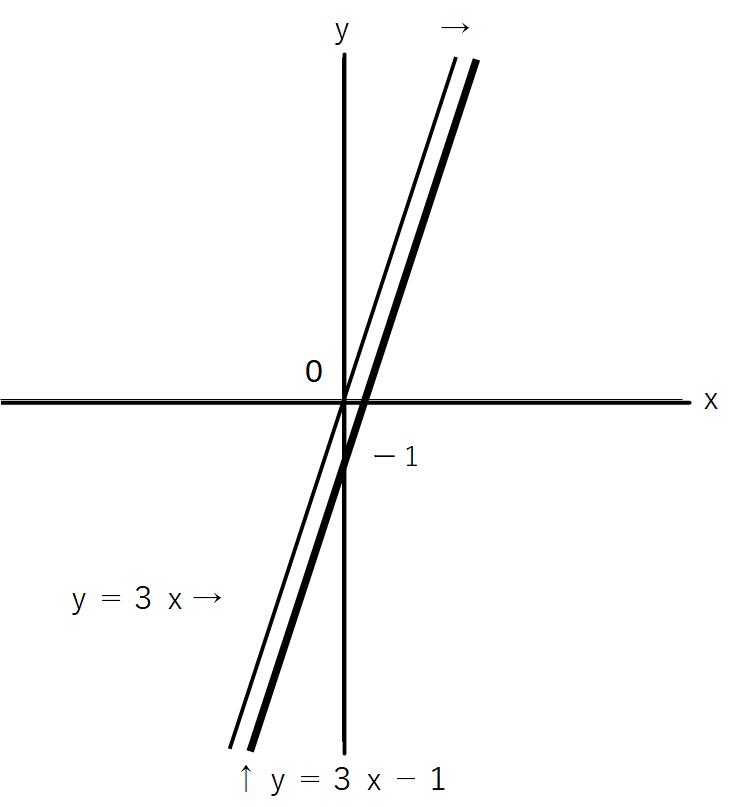
今度はy=3x-1のグラフです。
グラフを見ると、y=3x-1のグラフとは、y=3xのグラフをy軸方向でー1だけ平行移動させている、というグラフだといえます。
まとめます。

1次関数のグラフの書き方
書き方1)傾きと切片から書く
例)y=x-3
手順①
切片を定める
切片=y軸との交点=ー3
手順②
傾き=yの増加量/xの増加量
の式を使って直線の傾きを定める
この場合の傾き=1
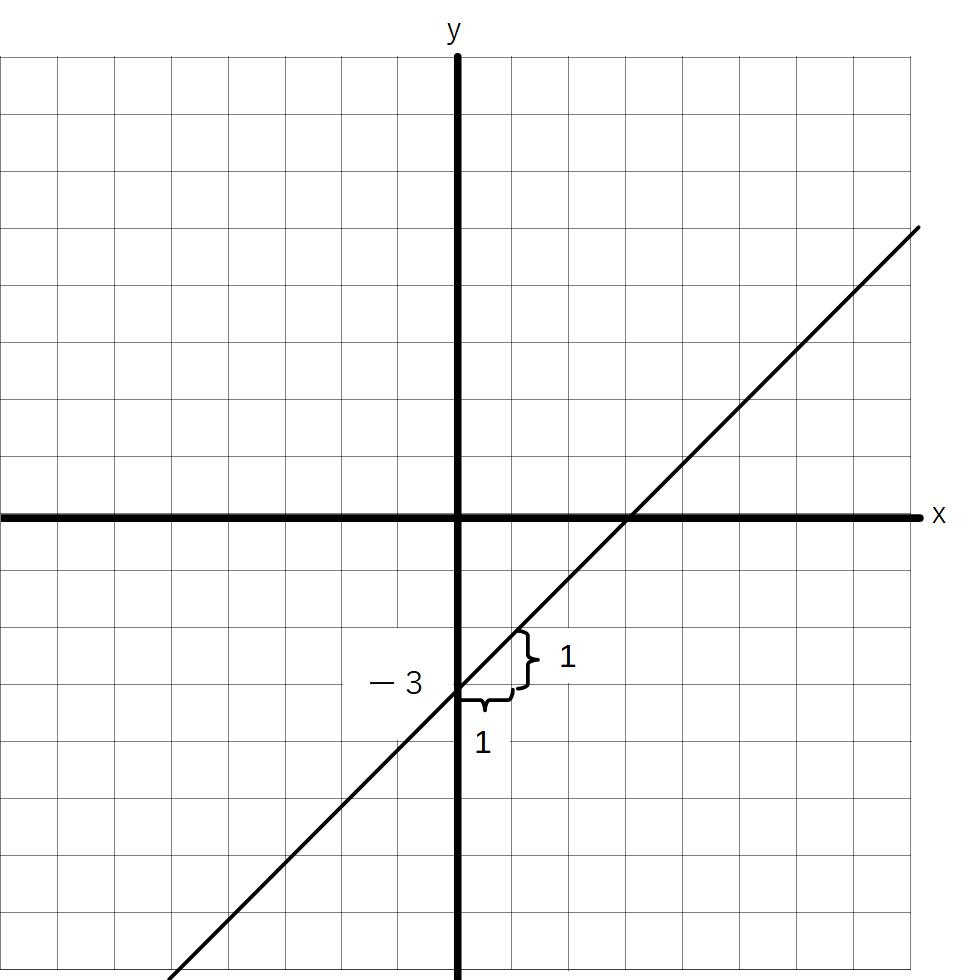
※表を作って1つ1つ点を打ってもグラフはかけますが、時間がかかります。そこで、上のように、切片と傾きを出して2点を決め、一気に書くという方法で引けるようにします。
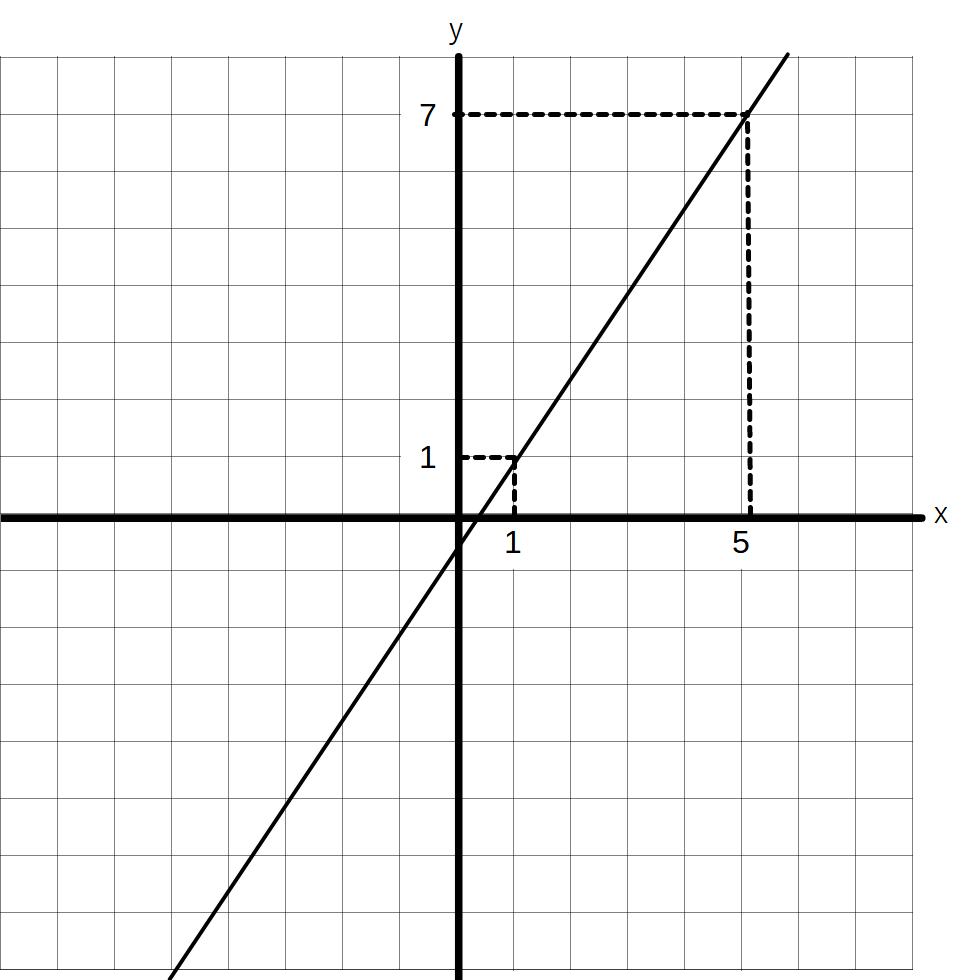
書き方2)直線を通る2点から書く
例)

1次関数のグラフの特徴と変域
(1)特徴
傾きが正の数→右上がり
傾きが負の数→右下がり
xの範囲(=変域)が定まった時、yの範囲(=変域)の取り方が変わってくる!
(2)変域
変域とは=x、yがそれぞれとることのできる値の範囲
→xの変域が定まれば、yの変域も当然に定まる(逆もまた同じ)
※変域はグラフを使って考える!
1次関数の変域については、グラフで考えなくても、数の代入によってできてしまいます。しかし、傾きの正負によって対応が逆になったりしますし、2次関数・3次関数(2次関数は3年で、3次関数は高校で学びます)になってくるとグラフによる理解が不可欠になります。グラフでイメージできるようになっておくとよいですので、できればグラフで理解できるようにしておきましょう。
例)
①傾きが正の数のとき
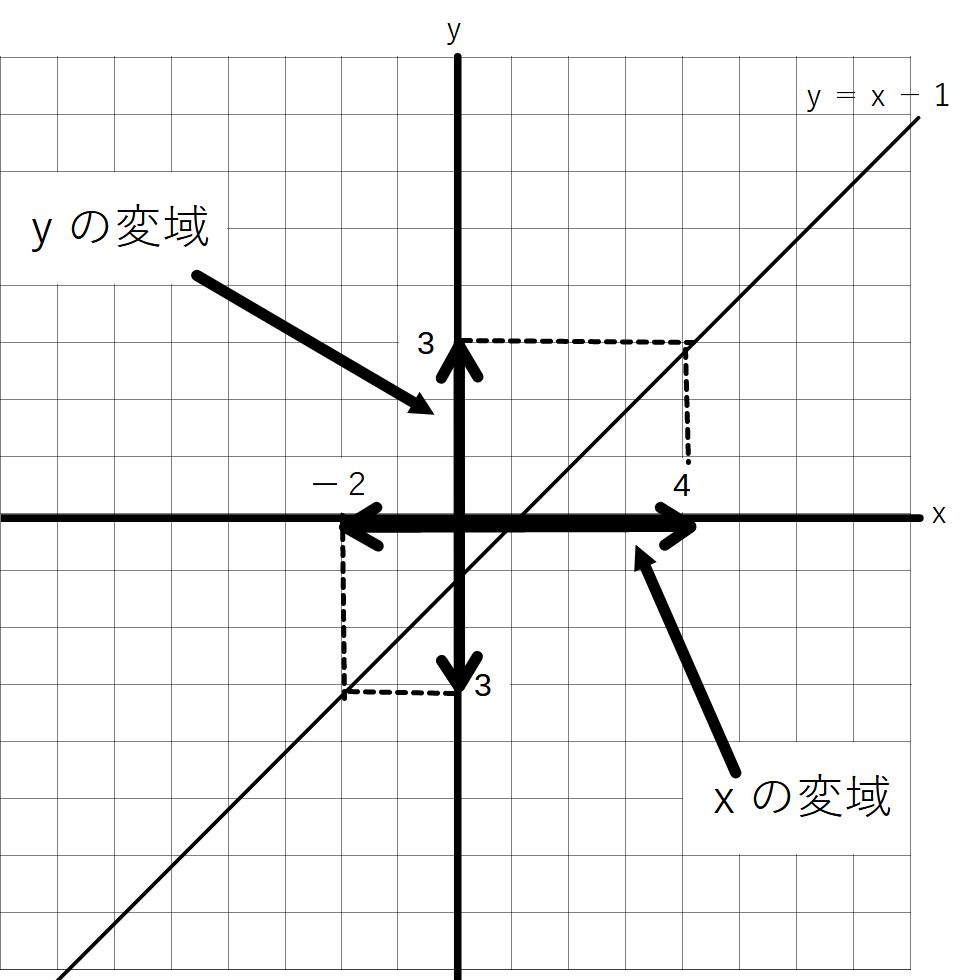
例)y=x-1で、
ー2≦x≦4のときのyの変域
x=ー2のときy=ー3
x=4のときy=3
よってー3≦y≦3
となる
②傾きが負のとき
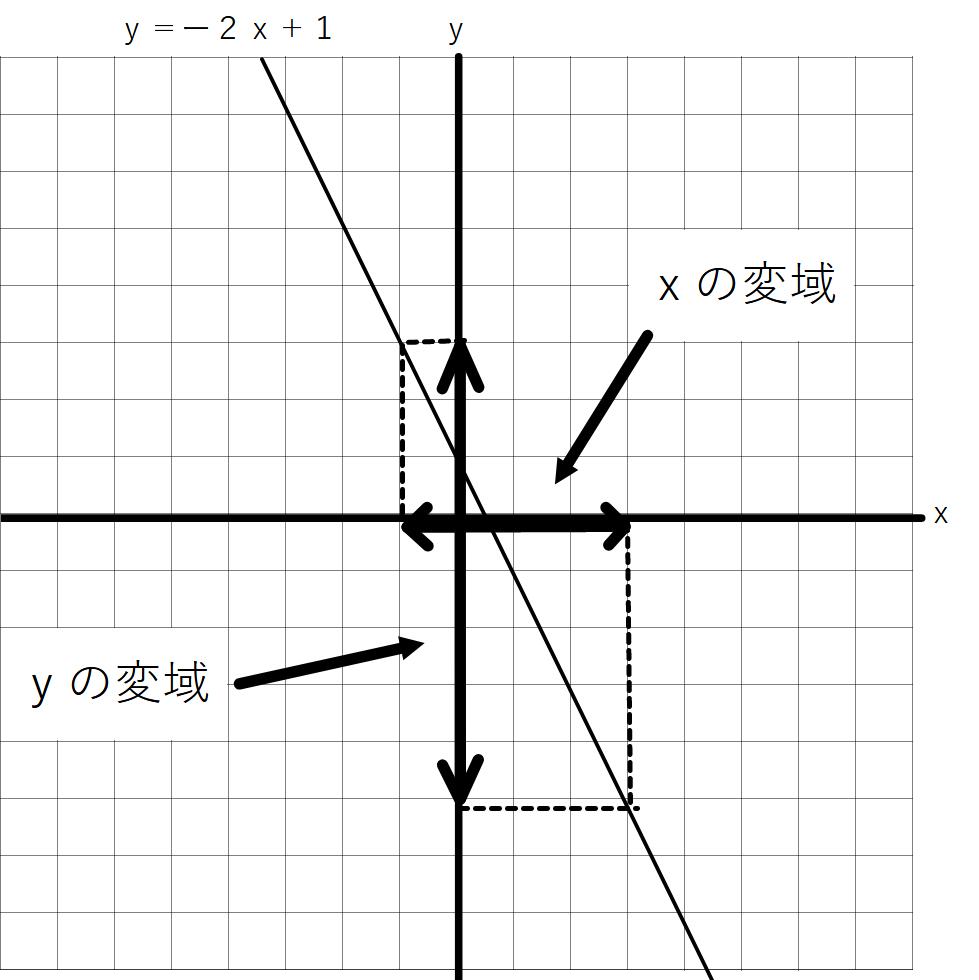
例)y=ー2x+1で、
ー1≦x≦3のときのyの変域
x=ー1のときy=3
x=3のときy=ー5
よってー5≦y≦3
となる