2元1次方程式とグラフ
(1)2元1次方程式 →グラフは直線になる!
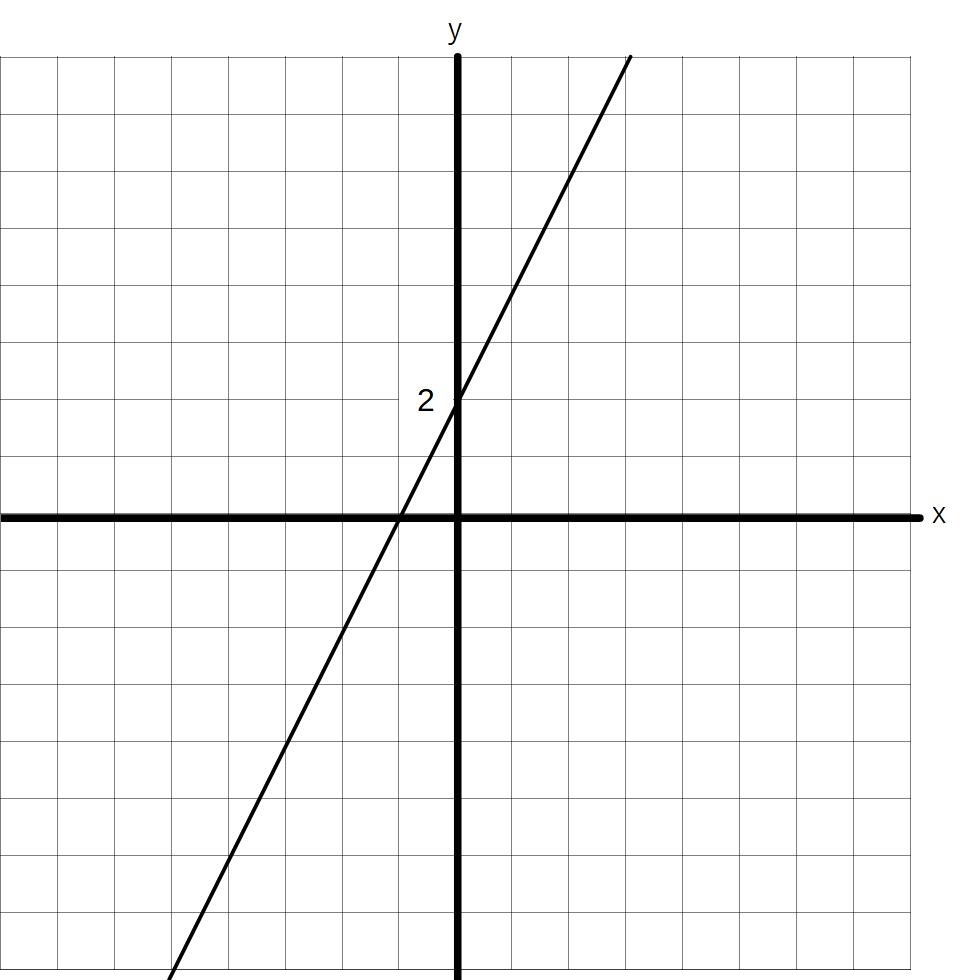
例)y-2x+y-2=0
yについて解くと、y=2x+2となり、
傾きが「2」、切片が「2」
①y-2x+y-2=0とx軸との交点
→式にy=0を代入 ー2x+0-2=0
x=ー1 よって(ー1,0)
②y-2x+y-2=0とy軸との交点
→式にx=0を代入 y-2=0 ∴y=2
よって(0,2)
※x軸との交点→y=0を代入する!
y軸との交点→x=0を代入する!
※2元1次方程式のグラフ
(1)2元1次方程式のグラフは直線になる
(2)2元1次方程式のグラフは
①2元1次方程式をy=ax+bの形に直して、傾きを切片を使って書く
②2元1次方程式とx軸、y軸の交点を求め、2点を通す
③(x、y)が整数となる2組の点を見つけ、その2点を通る直線を引く
(2)2直線の交点
例)次の方程式で示される2直線の交点を求めよ。
→この方程式をyについて解くと、下のようになります。
→さらに、それをグラフに書き出します。
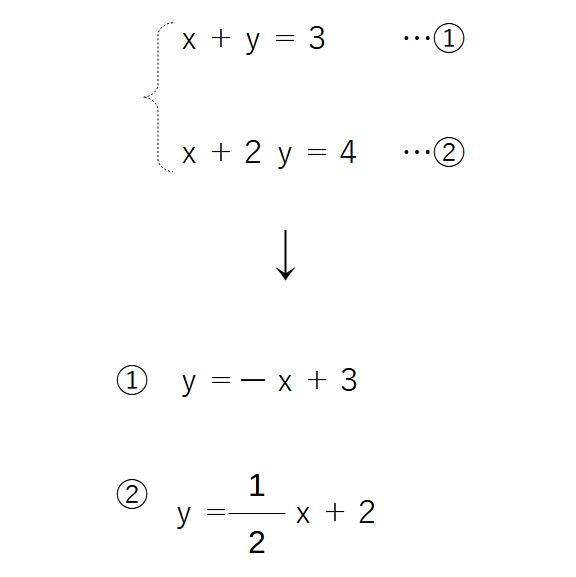
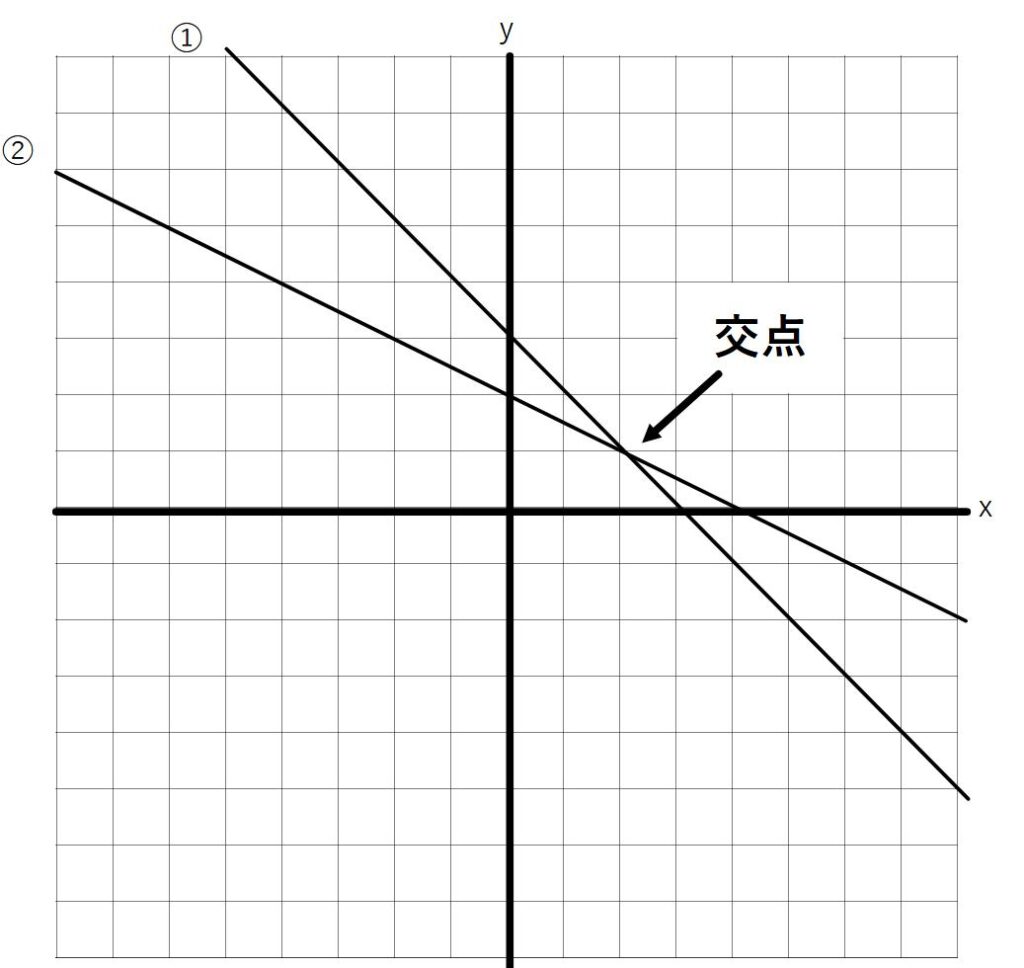
交点ができました。
この交点の座標xとyは、①と②の式の両方の数値を満たすといえます。(交点ということは、どちらの直線もその座標を通っているので)
→ということは、上の方程式を連立方程式として計算すればxとyの数値がわかる、つまり連立方程式として計算すれば2直線の交点が求まる、ということになります。
2直線の交点=連立2元1次方程式(連立方程式)の解
上記の①②の連立方程式を計算すると、x=2,y=1となります。実際にグラフで確認しても、(2,1)に交点があるのがわかります。
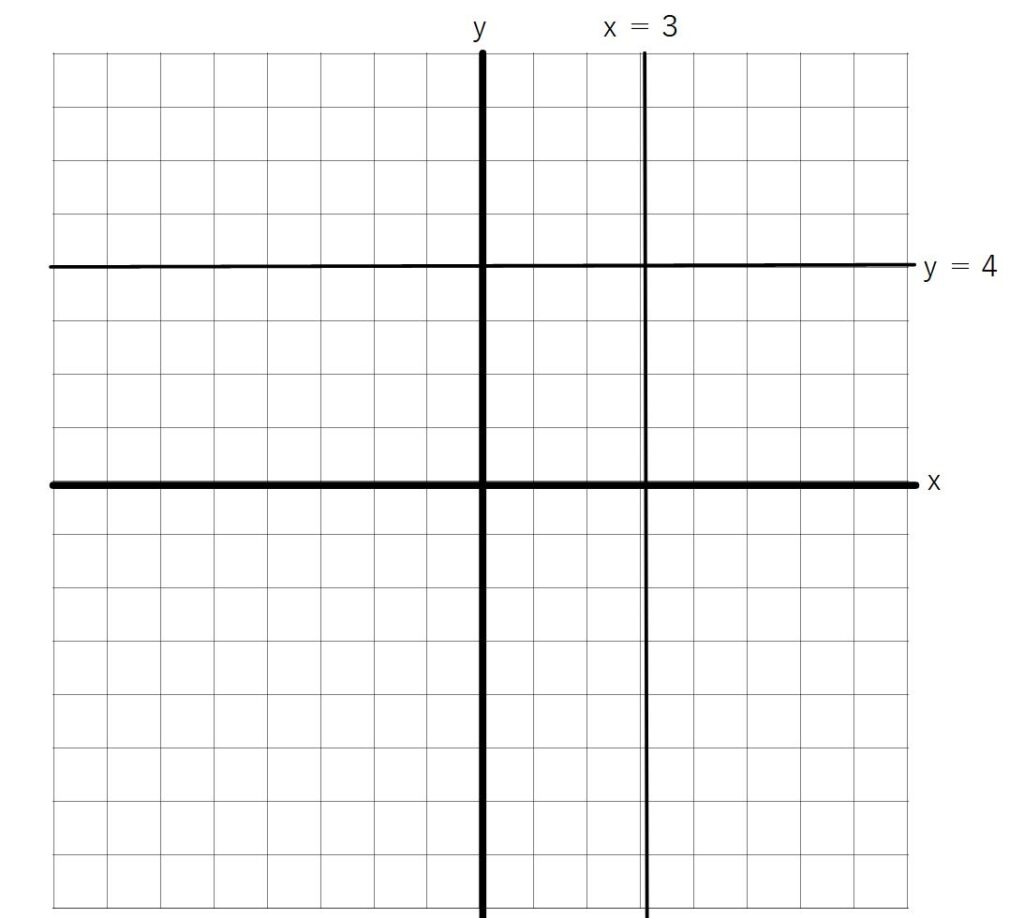
y=k、x=kのグラフ
①y=4のグラフ
→yの値はxの値がどんな値でも常に「4」
→x軸に平行に常にy=4
②x=3のグラフ
→xの値はyの値がどんな数でも常に「3」
→y軸に平行に常にx=3