(1)線分の長さ
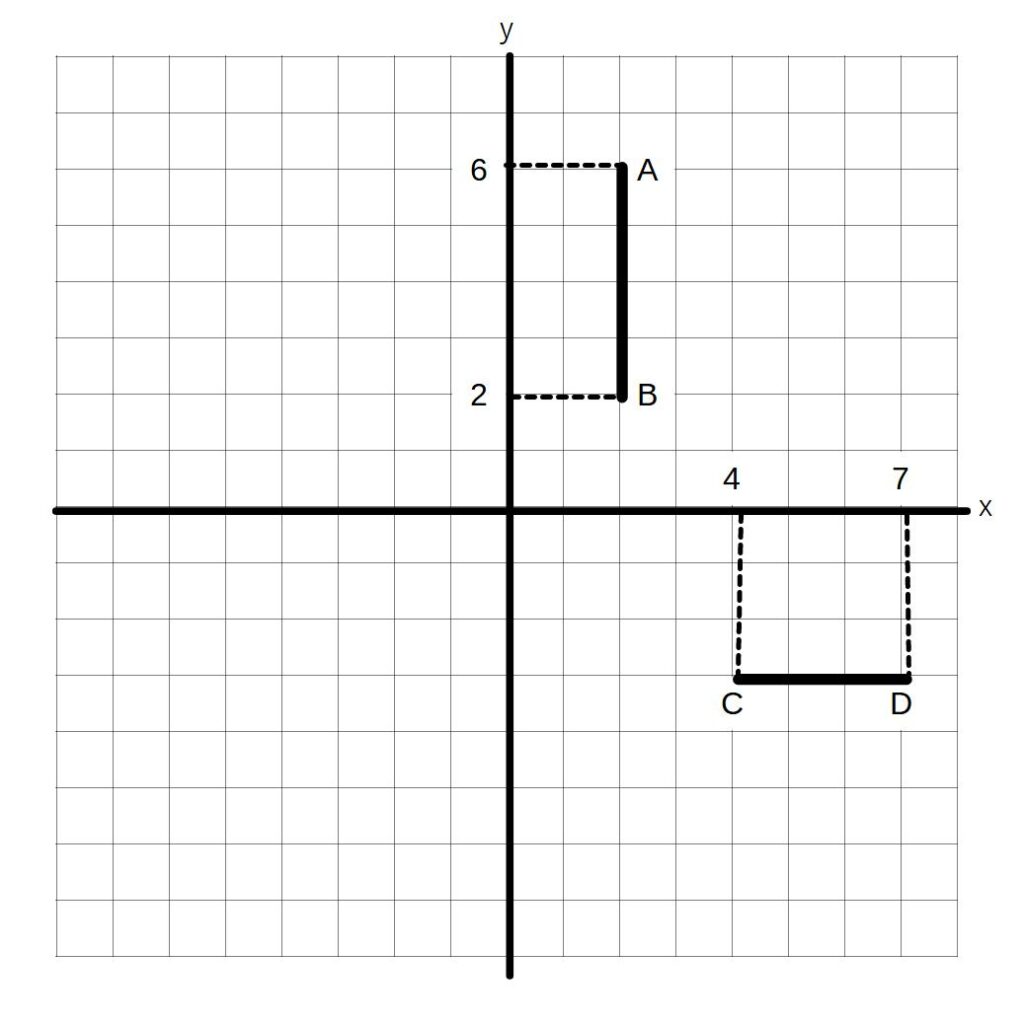
ABの長さ
Aのy座標ーBのy座標
6-2=4
CDの長さ
Dのx座標ーCのx座標
7-4=3
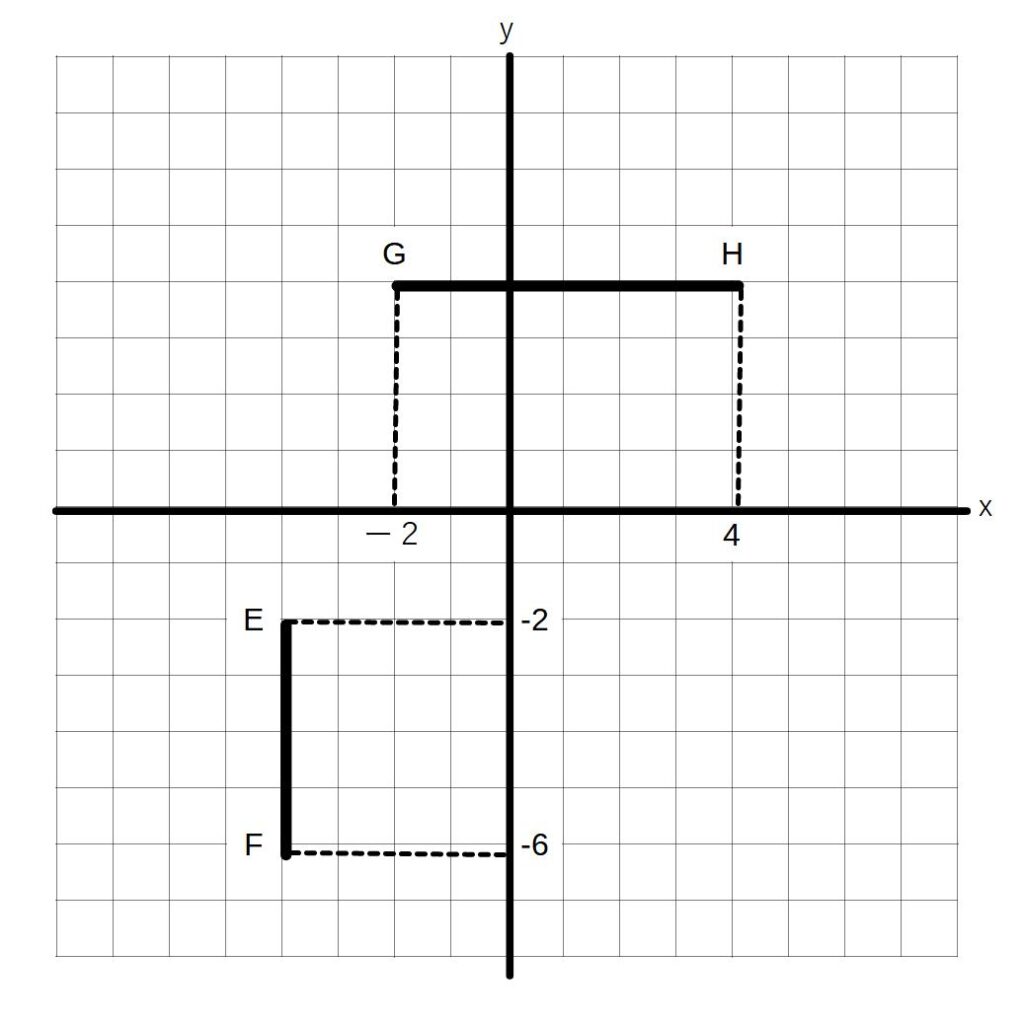
EFの長さ
Eのy座標ーFのy座標
(ー2)ー(ー6)=4
GHの長さ
Hのx座標ーGのx座標
4-(ー2)=6
※線分の長さ
①x軸に平行な線分の長さは両端2点のx座標の差
②y軸に平行な線分の長さは両端2点のy座標の差
③両方とも、(大きい座標)ー(小さい座標)の計算でOK
座標が正でも負でもOK
→わかっていなくても解けてしまう人が多いかもしれませんが、ふとした時に混乱するかもしれないので、このことは理解しておく方がよいでしょう。
(2)グラフと三角形
1.三角形の面積
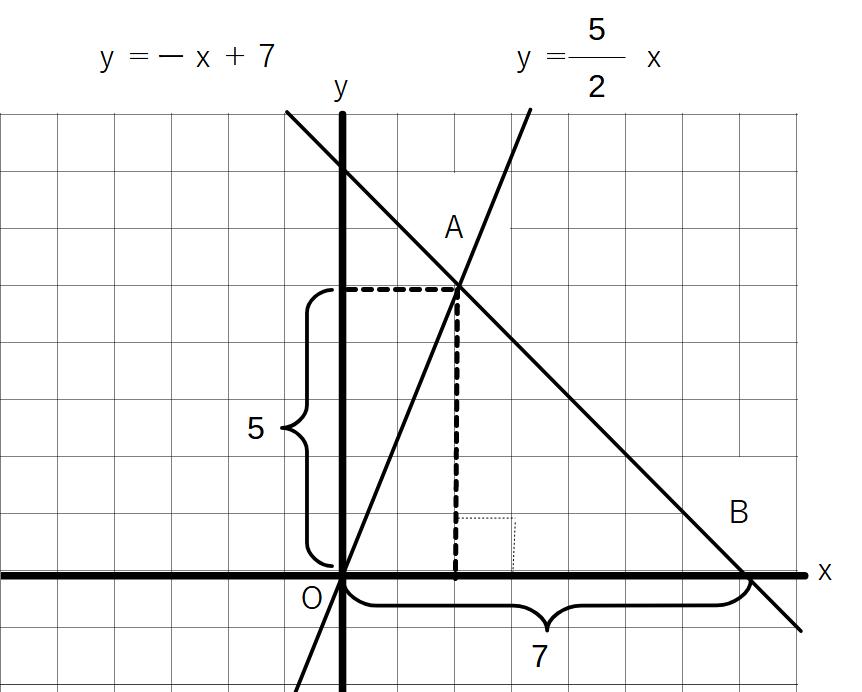
例①
△OABの面積
底辺をOBとすると、OBの長さ=7
高さは点Aからy軸に平行にとって、5
よって、7×5×1/2=35/2
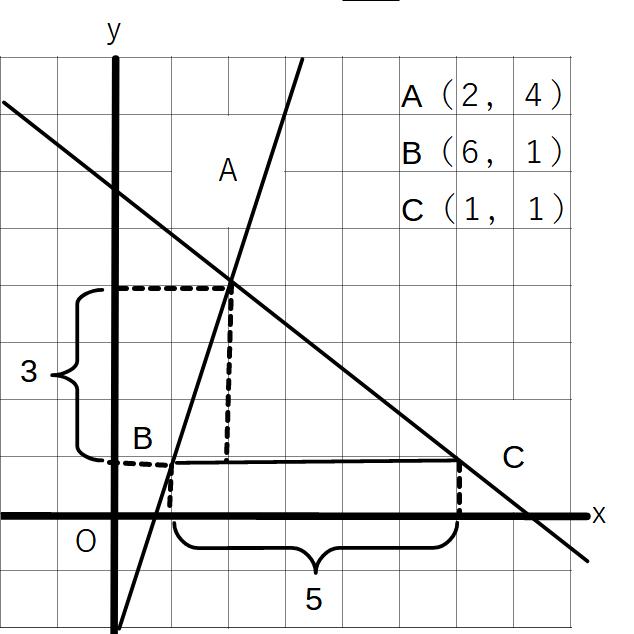
例②
△ABCの面積
底辺をBCとすると、底辺の長さ=5
高さは点Aからy軸に平行にとり3
よって、5×3×1/2=15/2
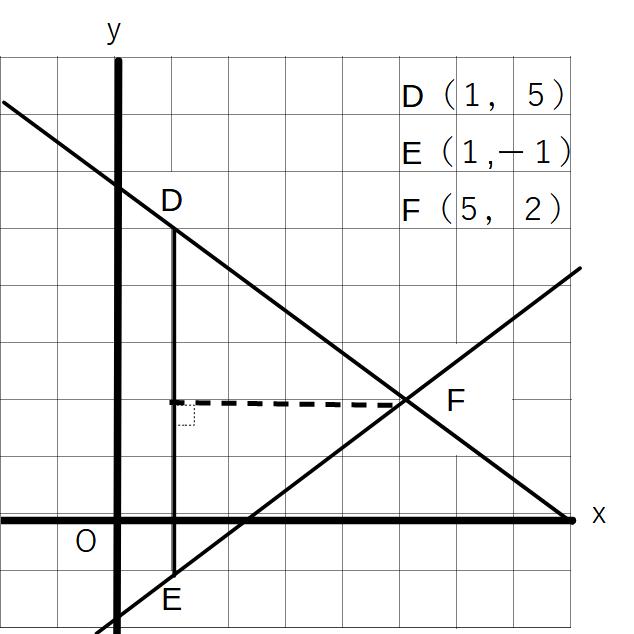
例③
△DEFの面積
底辺をDEとする→底辺の長さ=6
高さは点Fからx軸に平行で、4
よって、6×4×1/2=12
※底辺を軸に平行にとるようにしましょう!
例④△OABの面積を求めよ
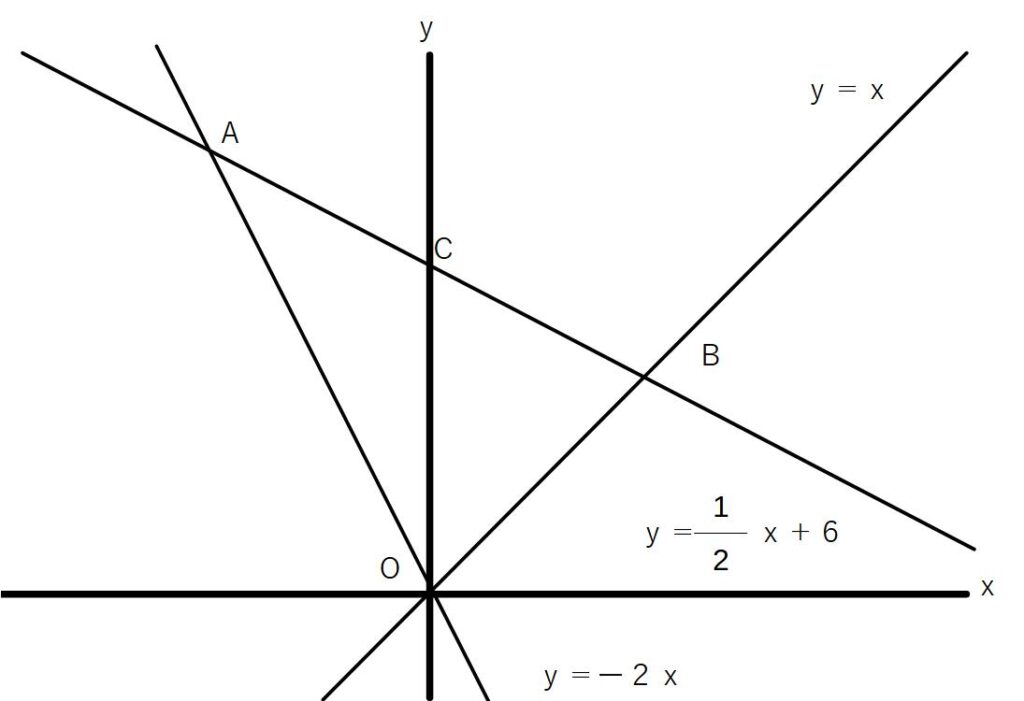
まずは点A、B、Cの座標を出す
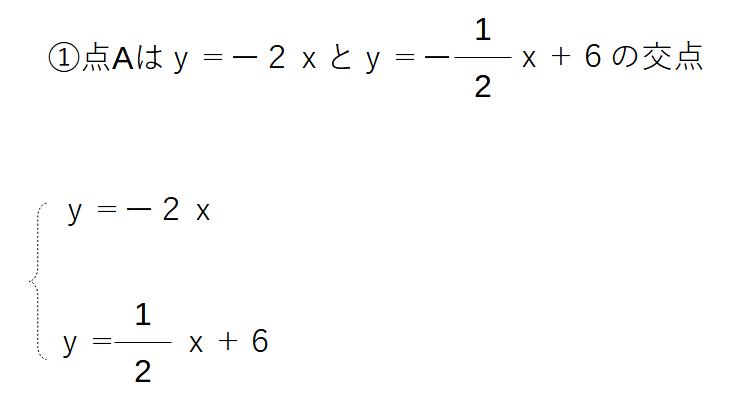
計算する→よって、x=ー4.y=8
点A(ー4,8)となる
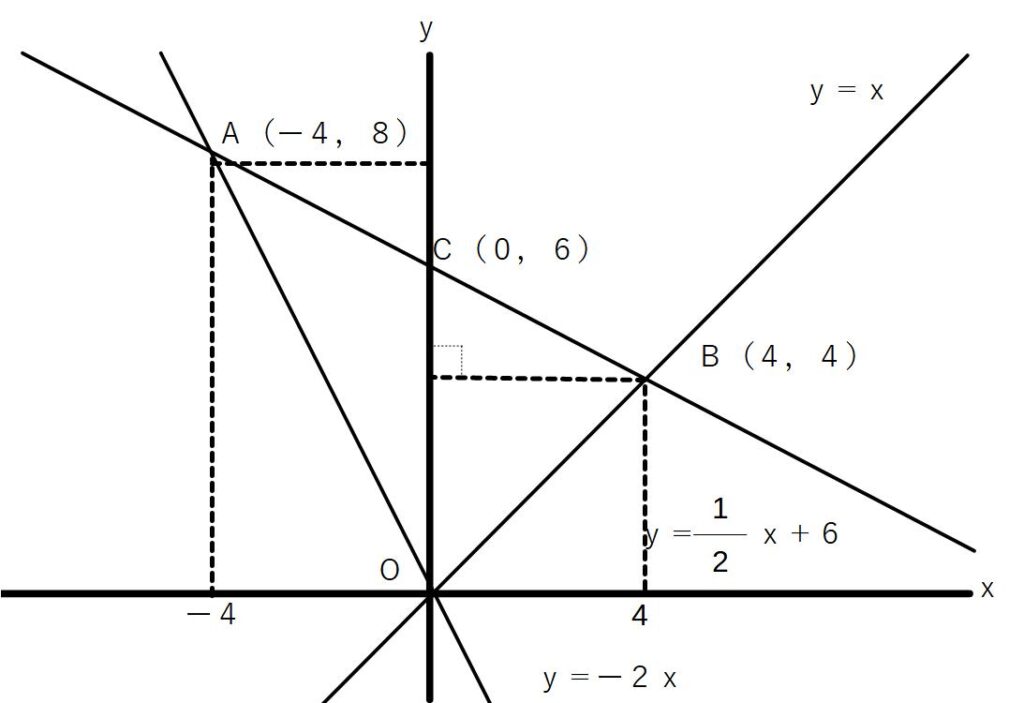

解法①線分OCを底辺として、△OACと△OBCの面積を出す
△OAC=6×4×1/2=12
※ただし、長さは正だから、高さは点Aのx座標の絶対値
△OAB=△OAC+△OBCなので、
△OAB=12+12=24
解法②(①の応用)→底辺を共通にとっているとき
△OAB=底辺×(高さの和)×1/2でもOK
△OAB=6×(4+4)×1/2=24
※座標上の三角形の面積を求めるときは、その三角形を囲むように長方形を作り、余分な三角形を引く、という方法を用いてもよい。
図の長方形(点線で囲んだ部分)から、斜線部分の三角形3つ分の面積を引く
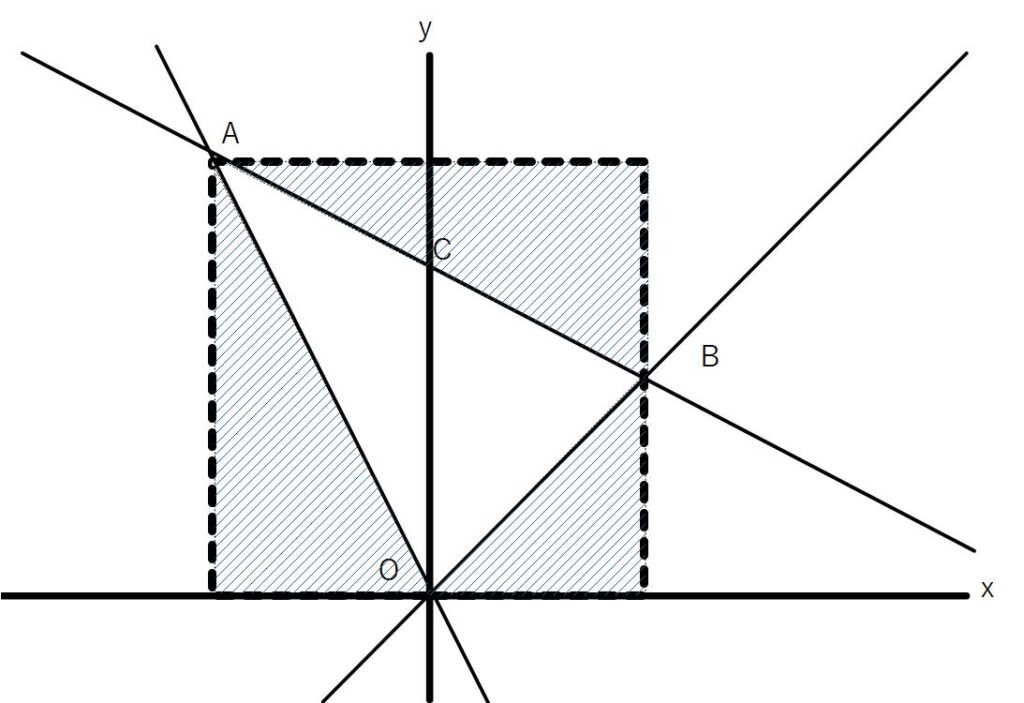
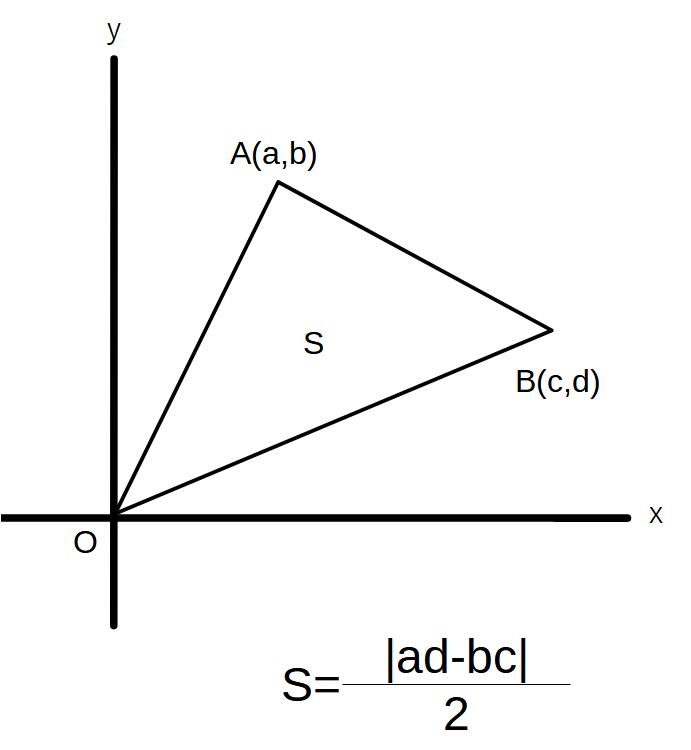
※原点を含む三角形の面積
この公式で一発で解けます。
ちなみに、|adーbc|の両側についている縦棒は、絶対値記号です。+ー考えないで数値を入れて計算してください。
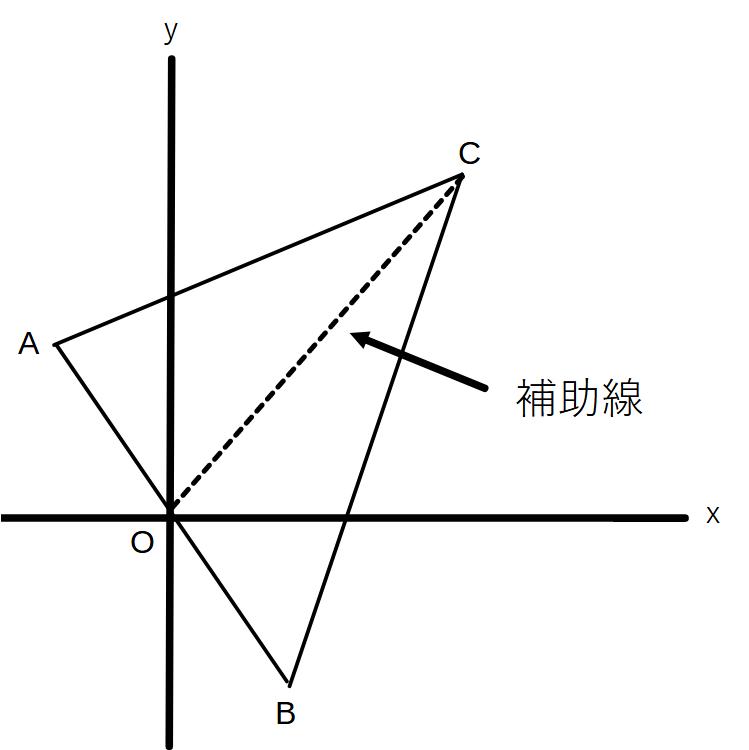
例えば、図のような三角形ABCの面積を求める場合、△OACと△OBCに分けて、先ほどの公式で面積を出して、さらにその2つを足すことで⊿ABCの面積を求めることができます。
2.三角形の面積を2等分する直線
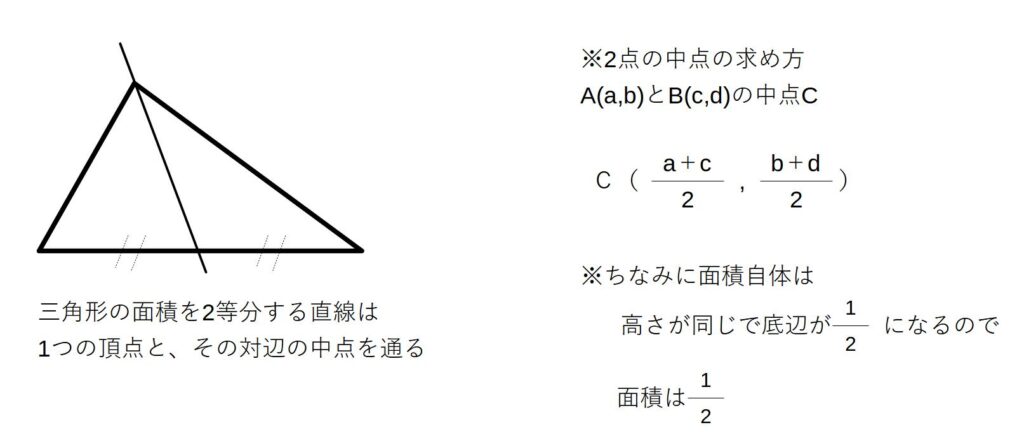
(3)グラフと平行四辺形
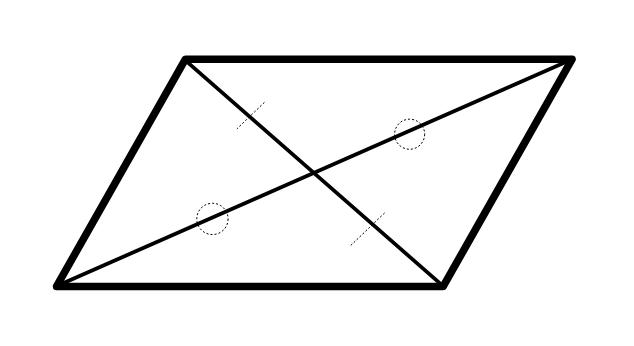
対角線の交点を通る直線はすべて平行四辺形を2分する!
平行四辺形の対角線はおのおのの中点で交わるので、交点の座標はは平行四辺形の一方の対角の座標がわかれば中点の座標を求めることで出せます。
※平行四辺形の性質
対辺が平行で、長さが等しい
(4)パラメータ~座標を文字を使って表す~

例)図のような直線がある。直線m、ℓはそれぞれ図に示された直線の式のグラフを表している。x軸上の点P(a、0)を通り、y軸に平行な直線が、2直線ℓ、mと交わる点をそれぞれQ,Rとする。
a>0として、次の問いに答えよ。
(1)a=4のとき、線分QRの長さ
(2)線分QRの長さが12となるようにaの値を定めよ。
①a=4ということは、P(4,0)ということになる。
点Q、点Rの座標はそれぞれ直線ℓ、mにx=4を代入する。

②ではP(a、0)のときの点Q、点Rをaを使って表す
→直線ℓ、mにx=aを代入して、y座標をを使って表す
これを使って、線分QRの長さを文字(a)を使って表す
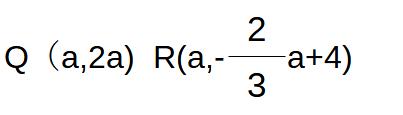
※a>0で、QR=12になるのは図のような場合
=(点Qのy座標)>(点Rのy座標)なので
y軸に平行な線分の長さ=
(y座標の大きい方)ー(y座標の小さい方)
よって、図の計算の通り

※パラメータの解法
①座標を文字を使って表す
→数字の時と同じく直線の式に代入して、文字を使って座標を表すだけ!
②線分の長さを表す
→座標が文字でも長さの出し方は変わらない!
(5)グラフと四角形
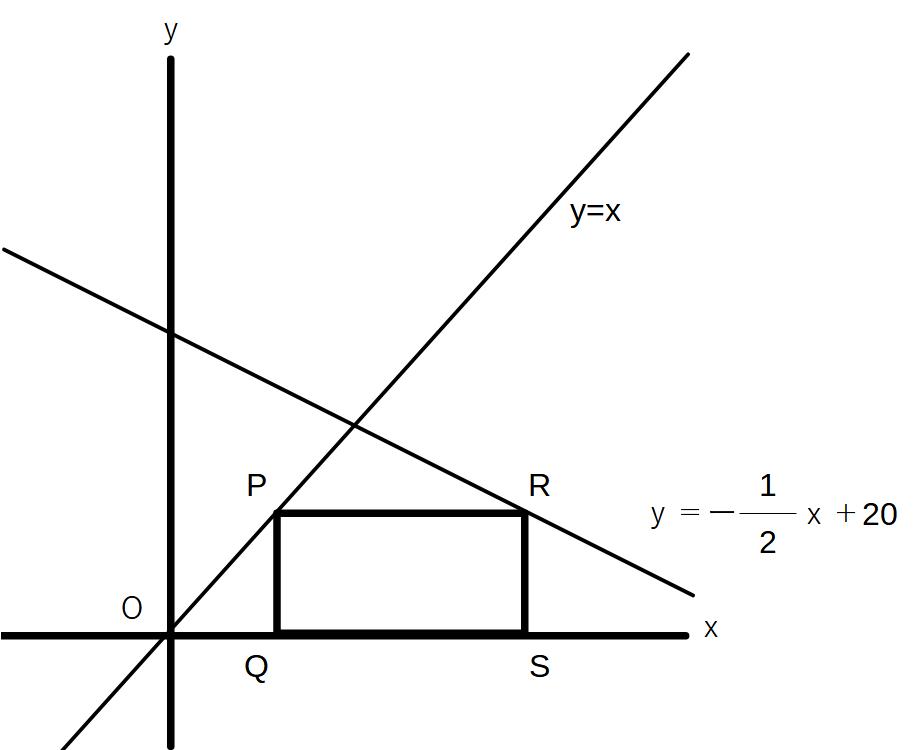
図の通りの直線があり、それぞれの直線のx軸に平行になる任意の点をそれぞれ点P、点Sととり、それをx軸に向かい垂直に垂線を下ろし、できた四角形PQRSとおく。次の問いに答えよ。
(1)四角形PQRSが正方形になるときの点Pの座標を求めよ。
(2)PR=2PQとなるときの、点Pの座標を求めよ。
座標を文字を使って表すことがポイントになります。
点Pのx座標をtとおく
点Pはy=x上にあるから、
P(t、t)となります。
ここで、Pの座標をうまく使ってほかの点が出せないか考えてみてください。
①PQはx軸に垂直=y軸に平行=QとPはx座標が同じ
また、Qはx軸上にあるから、
Q(t,0)となります。
②PRはx軸に平行=RとPはy座標が同じ(t)
また、Rはy=1/2x+20上にあるから、
t=-1/2x+20
x=40-2t
よって、R(40-2t,t)←このように、文字で表したまま、線分の長さを考える!
PQ=t
RP=40-2t-t=40-3t
(1)四角形PQRSが正方形なので、
PQ=RPとならないといけません。
よって、
t=40-3t
t=10
点Pは(t、t)だから、
P(10,10)となる
(2)PR=2PQということなので
40-3t=2t
t=8
P(8,8)となる
(6)ダイヤグラム
例)A君は、朝7時30分に家から2㎞離れた中学校へ向けて出発し、1km先の文具店まで走って向かい、10分後に文具店に到着しました。そこで5分休憩を取り、そこから歩いて中学校へ向かい、35分後に中学校へ到着しました。次の問いに答えなさい。
(1)家から文具店までのA君の歩く速さを求めなさい。
(2)A君の母親が忘れ物を届けるために、7時50分に家を出て時速18kmで追いかけました。母親がA君に追いついたのは何分後か答えなさい。
※横軸→時間・縦軸→移動距離・直線の傾き→速さ
単位量あたりの大きさは、基本的に傾きになることを覚えておきましょう。
※時間・距離・速さを利用すれば、式を立てなくてもグラフがかける
→問題文を読んだだけでもかける場合がある
※折れ曲がったグラフができるが、惑わされることなく、直線に範囲を限定してグラフを読み取る
→水平の部分は「止まっている」ということ
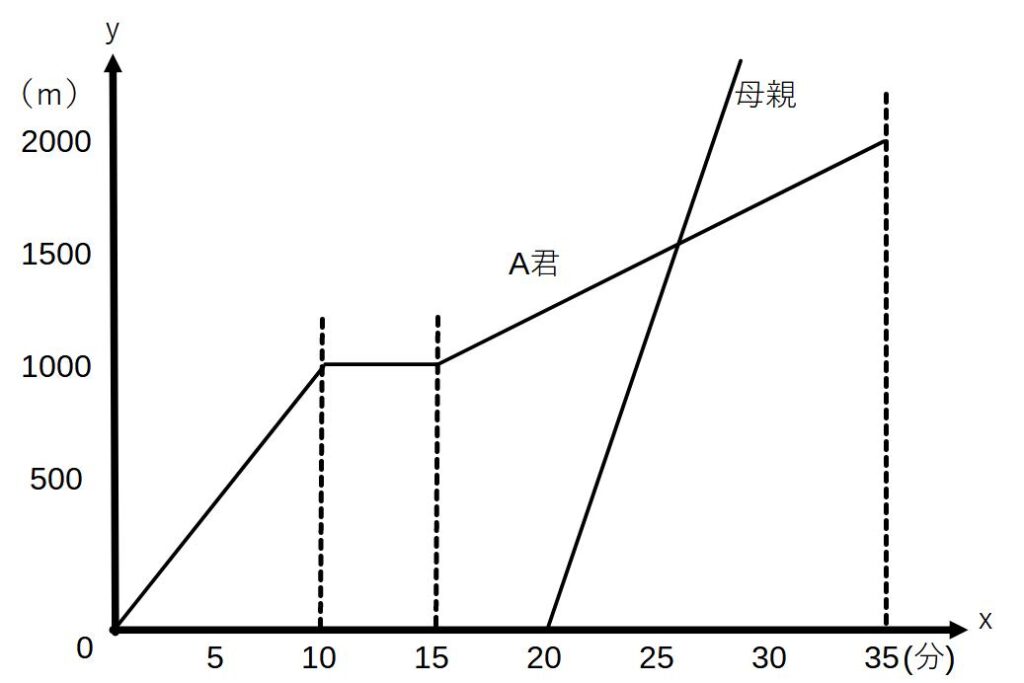
まず、グラフを書いてみます。
5分間休憩のところで水平になっています。
(1)家から文具店までのA君の速さ
→店に着くまで(0~10分)のグラフの傾き
y=100x(0≦x≦10)
よって、毎分100mとなる。
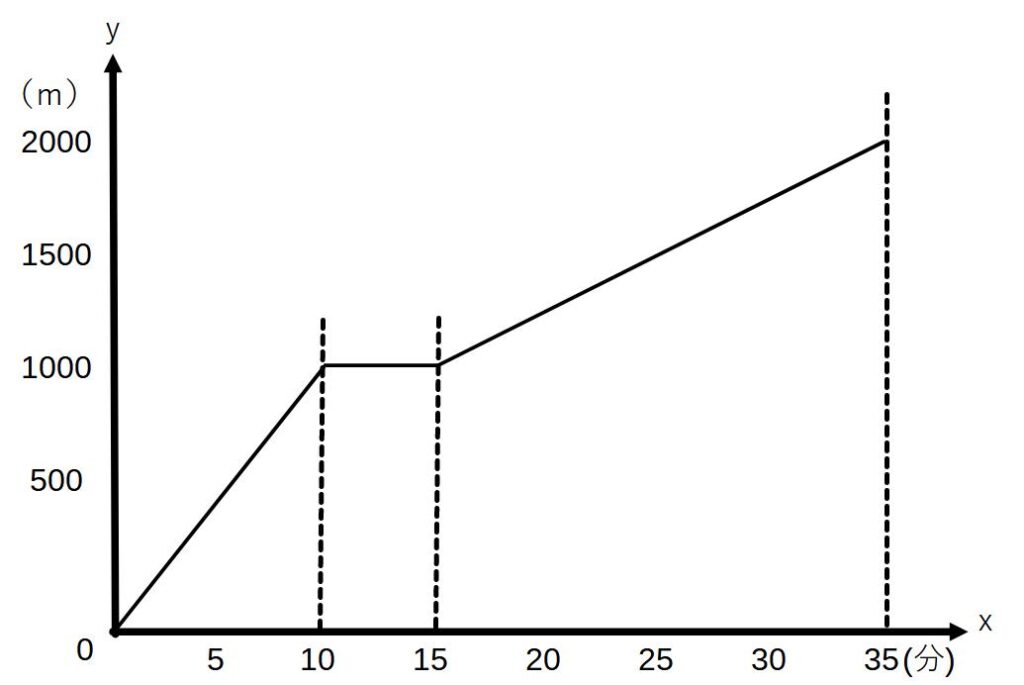
つづいて、母親が追いかけてきたグラフを足します。
(2)母親が7時50分に家を出てA君を時速18kmで追いかけた
①母親の分速 時速18000m÷60分=分速300m
点(20,0)が出発点で傾きが300
→グラフもかけるし、式も出せる
「かけちぇんたす」やってみましょう。
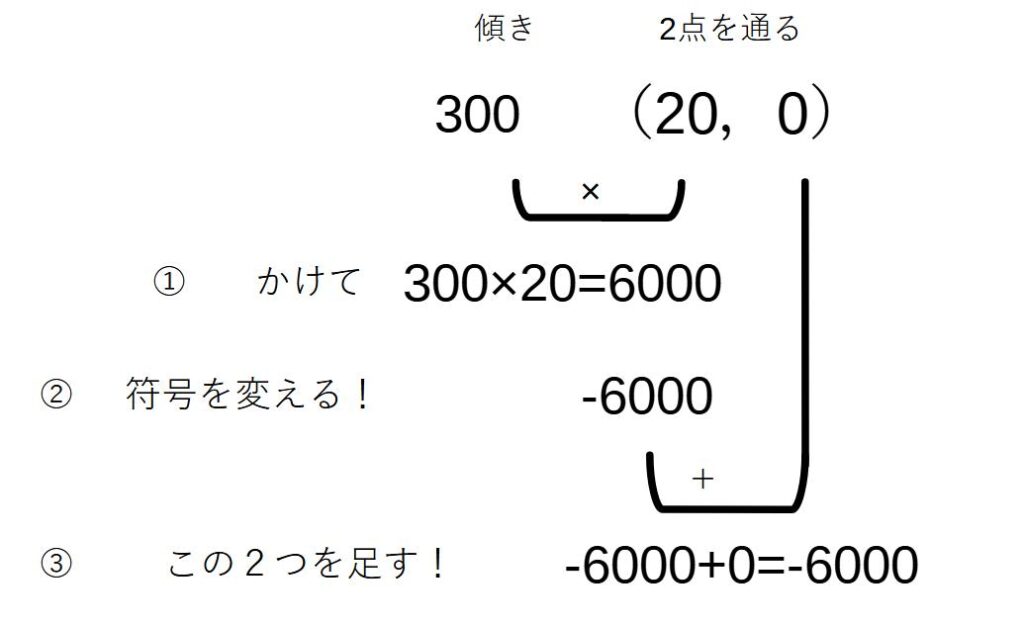
図の通り、傾きと切片が出ました。母親の進む直線の式は
y=300x-6000…①
となります。
②グラフの交点が、母親が追いついたところ!
→A君のグラフも出します。
A君のグラフは、15≦x≦35のところのグラフ
(15,1000)と(35,2000)を通る直線の式
y=50x+250…②
③①、②の交点を連立方程式で計算する
300x-6000=50x+250
∴x=25
④A君が出発してから25分後、7時55分に母親は追いつく
(7)動点
図のような長方形ABCDがある。点PはAを出発し、辺AB、BC、CD上を毎秒x㎝の速さで動く。以下の時の三角形APDの面積をyをxの式で表せ。
①辺AB上にいるとき
②辺BC上にいるとき
③辺CD上にいるとき
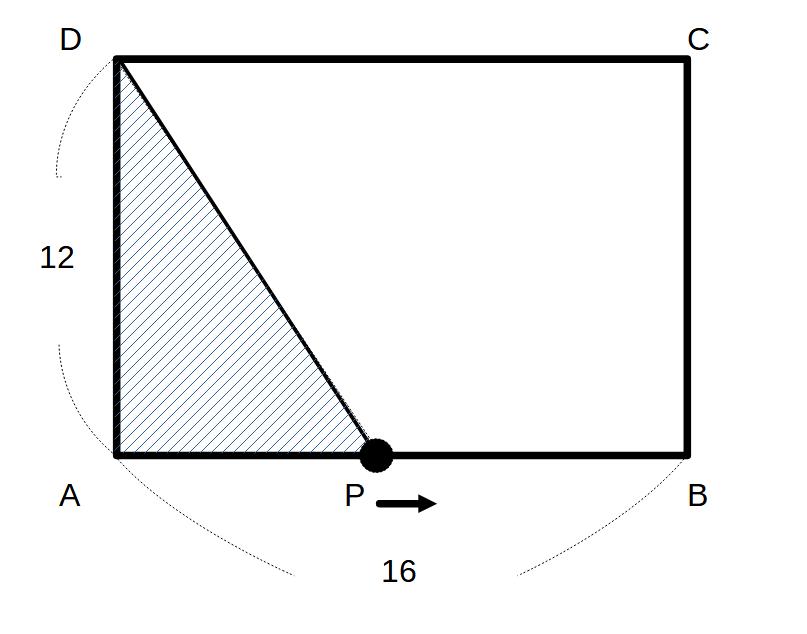
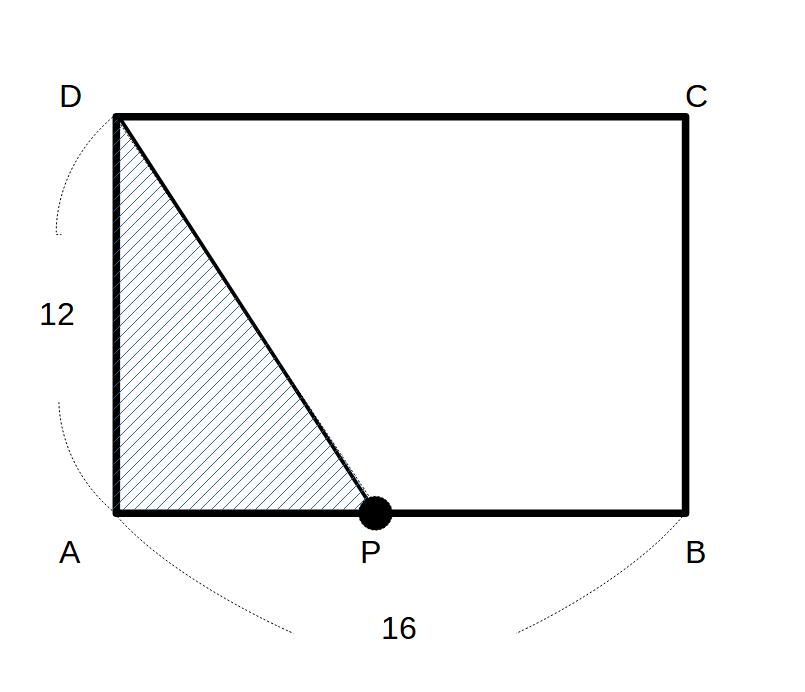
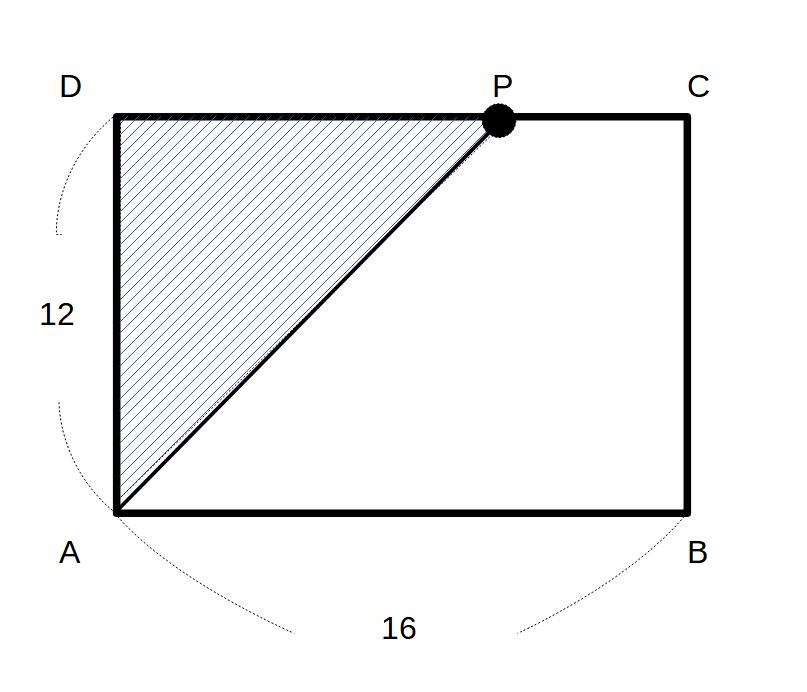
①Pが辺AB上にいるとき
0≦x≦16
y=12×x×1/2=6x
∴y=6x
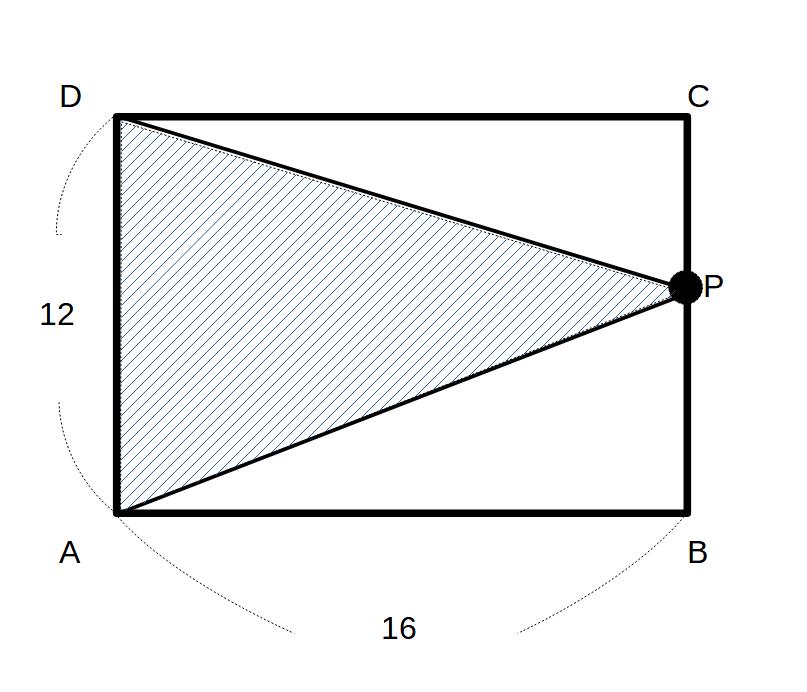
②Pが辺BC上にいるとき
16≦x≦28
この場合、高さ(AB=DC)は常に一定(16)なので、
y=12×16×1/2=96
∴y=96
③Pが辺CD上にいるとき
28≦x≦44
今回は高さが減っていくので、点A→点Dまでの全距離からxcmずつ減っていくと考えて式を作ります。
y=12(44-x)×1/2=6(44-x)
=ー6x+264
∴y=ー6x+264