(1)矢じり
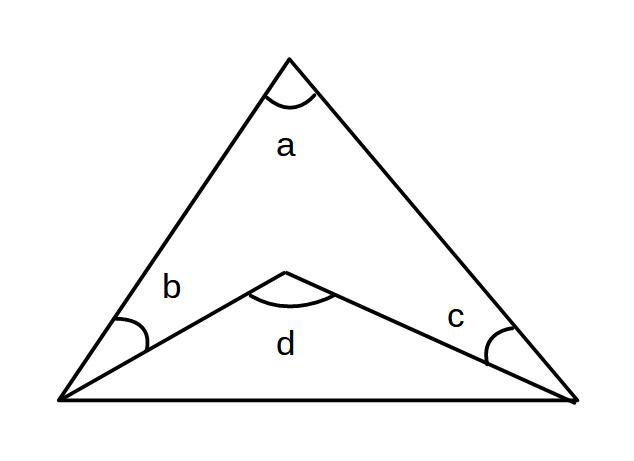
a+b+c=d
教科書では補助線を引いて矢じりの角度の出し方をやっていますが、この方法を覚えておくと便利なので紹介します。
(2)星
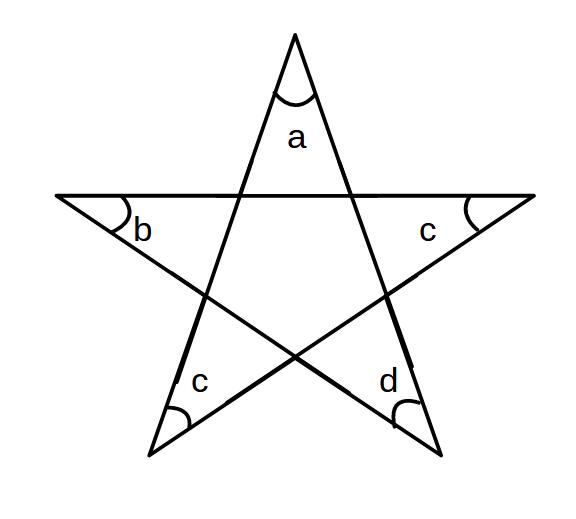
a+b+c+d+e=180°
この角度も覚えておきましょう。
ちなみに、この角度の証明については、前回やった外角の和を使って証明できます。(スリッパを見つけるやつです)
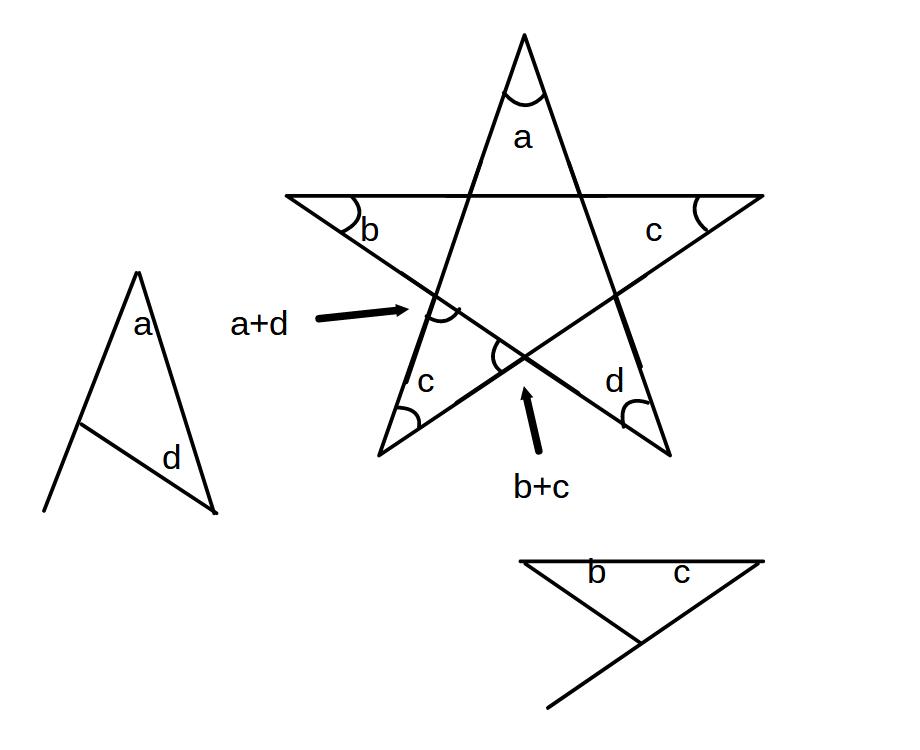
まず、この星型の中で、スリッパになる形を見つけます。
(今回は∠cについて考えます。)
∠cのある三角形の角はそれぞれ、図の通りスリッパの外角になることがわかります。
そうすると、∠cのある三角形の中にabcdeすべての角度が入ることになります。
また、三角形の内角は180°なので、a+b+c+d+e=180°が成り立ちます。
(3)リボン
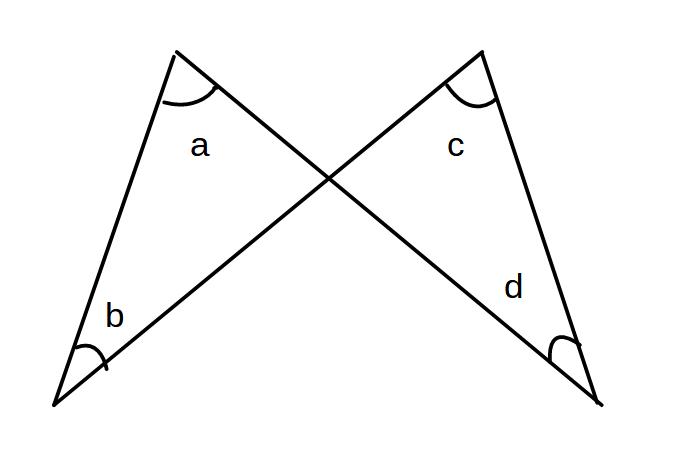
a+b=c+d
aとc(あるいはcとd)が等しい必要はありません。
あくまで2つの角度の和同士が等しいということです。
※ちなみに、これもスリッパまたは対頂角と三角形の内角の和で証明ができます。
ちょっと問題をやってみましょう。アプローチ方法など学びましょう。
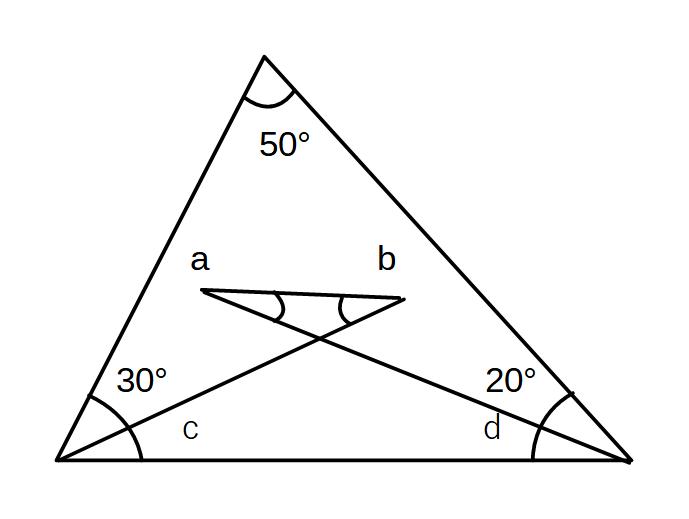
①aとbの和を求めよ。
50+30+c+d+20=180
c+d=80°
a+b=c+dより
a+b=80°
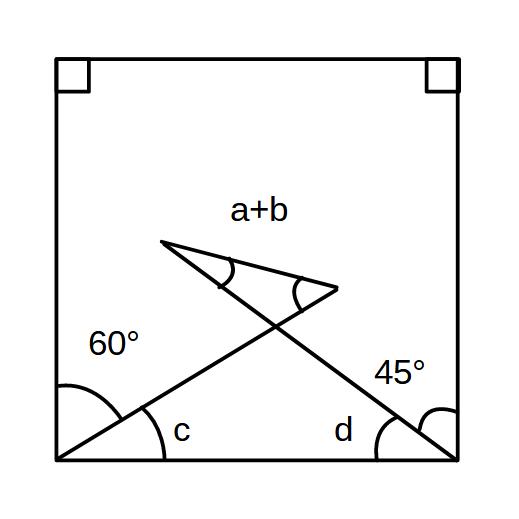
②aとbの和を求めよ。
90+90+60+c+d+45=360
c+d=75°
a+b=75°
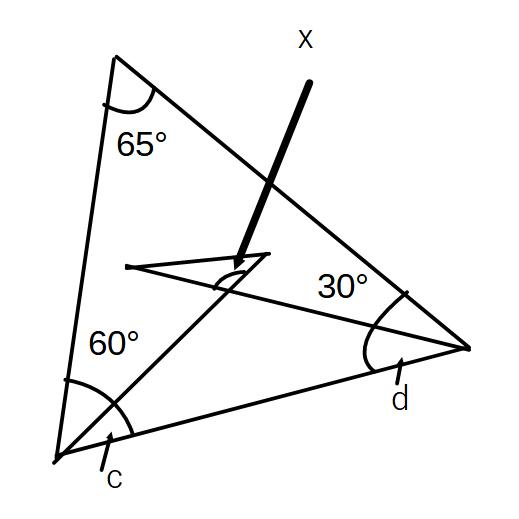
③xを求めよ。
65+60+c+d+30=180
c+d=25°
x=180-(c+d)=155°
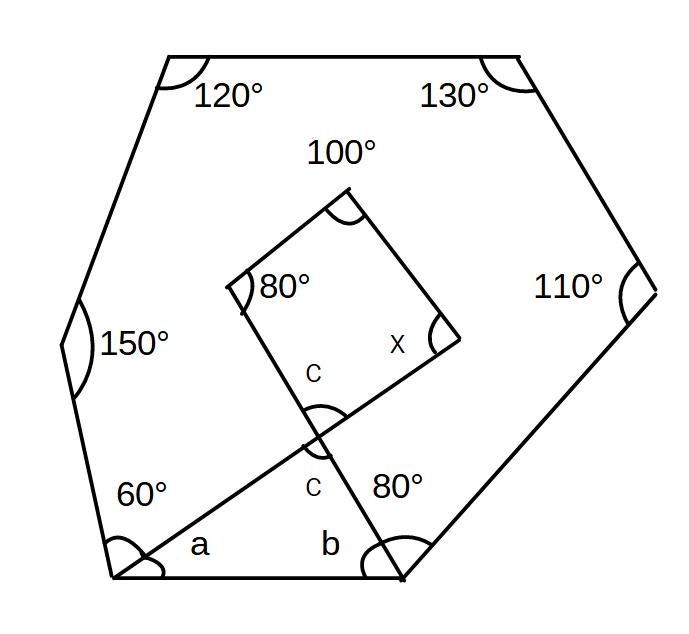
④xを求めよ。
120+150+60+130+110+80+a+b=720
a+b=70
c=180-70=110
x=360-(100+80+110)
x=70°
(4)2つの角の二等分線
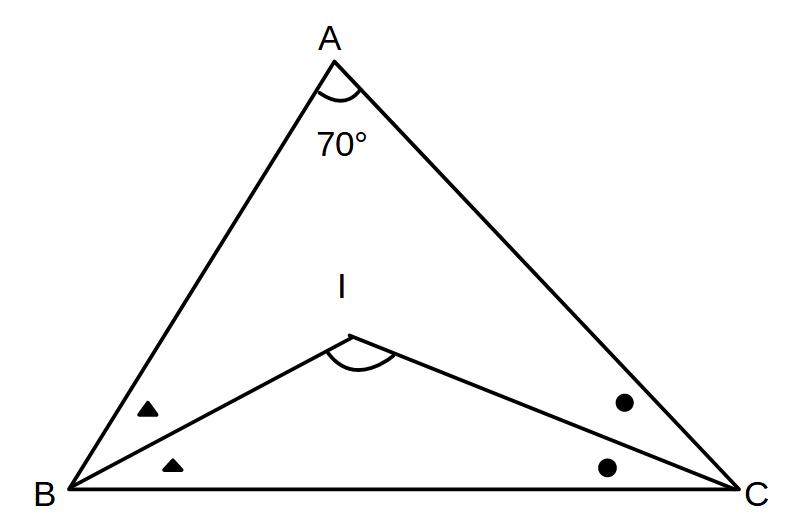
例1)
∠BAC=70°でかつ
∠ABCの二等分線と∠ACBの二等分線の交点をIとするとき、
∠BICの角度xを求めよ。
解)①△ABCの内角の和=180°より、▲+▲+●+●=180°ー70°=110°
②▲、●はそれぞれ∠ABC、∠ACBの半分だから、▲+●=110°÷2=55°
③△IBCの内角の和=180°
x=180°ー55°=125° ∴x=125°
※①三角形の外角を上手に見つけて利用する
②1つ1つの角度がわからなくても、2つの角の和を利用できるときは、それを使ってほかの角度を求める
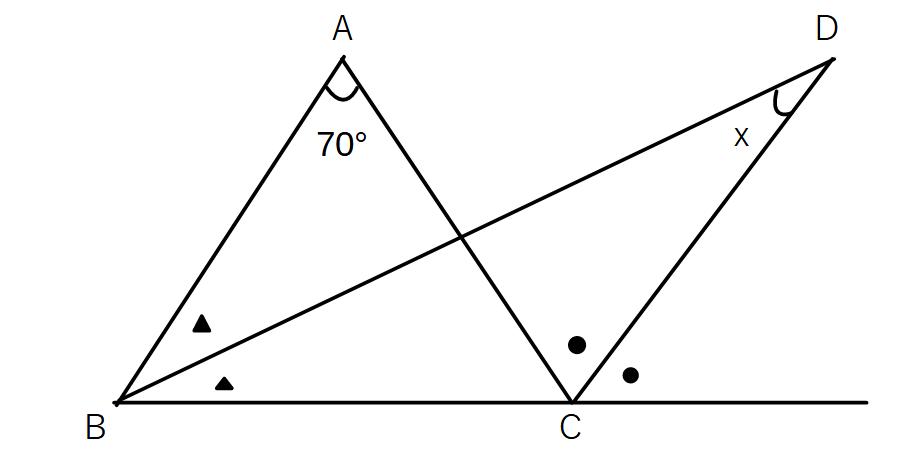
例2)xを求めよ。
▲=a、●=bとすると
2a+70°=2b…① (←△ABCの外角)
a+x=b…② (←△BCDの外角)
①→2b-2a=70°
b-a=35°
②→x=b-a
①、②よりx=35°