(1)仮定と結論
①結論…最終的にたどり着いた結果のこと。
②A(仮定)ならばB(結論)という関係が成り立つ
(2)証明
結論までにたどり着く道のり(理由)を筋道を立てて説明していく
(3)証明の仕方
例)
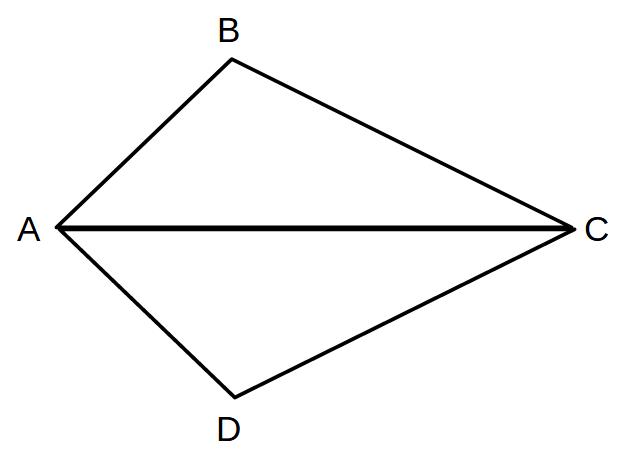
AB=AD、∠BAC=∠DACのとき、
△ABC≡△ADCを証明せよ。
例)の証明
△ABCと△ADCにおいて、
仮定より、AB=AD…①
∠BAC=∠DAC…②
共通する辺より、AC=AC…③
①②③より、
2組の辺とその挟む角が等しいので、
△ABC≡△ADC
←まず、どの三角形を使うかを明確にする
←次に、問題文からわかっていることでかつ、条件に必要なことを書き出していく
←同じ辺なので、共通する辺であるにきまってる
←どの条件を使って合同を証明するのかを明確にする
←合同条件への当てはめ
←結論
※①問題文の中から仮定を見つけ出す
→例)によればAB=AD、∠BAC=∠DAC
②平行線と角、三角形の内角と外角など、図形の性質などから等しい辺や角度を見つけ出す
③①、②で見つけた等しい辺、等しい角を三角形の合同条件に当てはめる
④結論を書く
→対応する辺や角はきちんと順番をそろえる!
※問題では、与えられた図形に等しい辺や角を記入し、対応関係や合同条件を探すようにする。
例1)
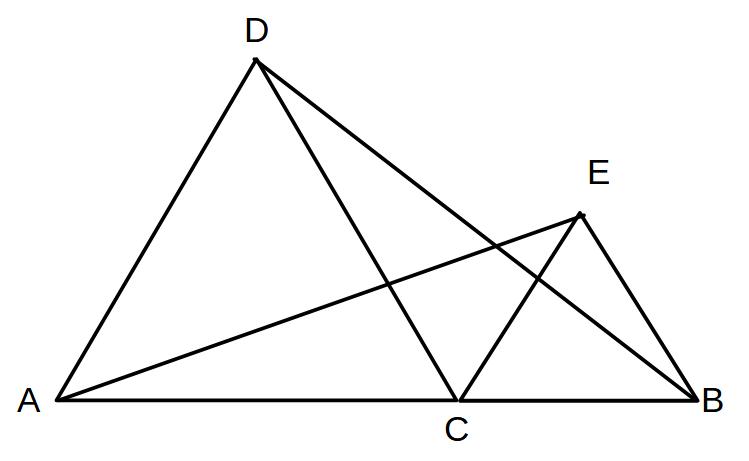
2つの正三角形ACDとBCEがあり、図のように線が引かれている。
△ACE≡△DCBを証明せよ
ヒント
∠ACE=∠ACD+∠DCE
∠DCB=∠BCE+∠DCE
∠ACD=∠BCE=60° ←これを使う
(証明)
△ACEと△DCBにおいて
仮定より、(△ADC,△BCEは正三角形なので)
AC=DC…①
CE=CB…②
また、
∠ACE=∠ACD+∠DCE…③
∠DCB=∠BCE+∠DCE…④
∠ACD=∠BCE=60° …⑤(仮定)
③、④、⑤より、
∠ACE=∠DCB…⑥
①、②、⑥より2組の辺とその挟む角が等しいので、
△ACE≡△DCB
例2)
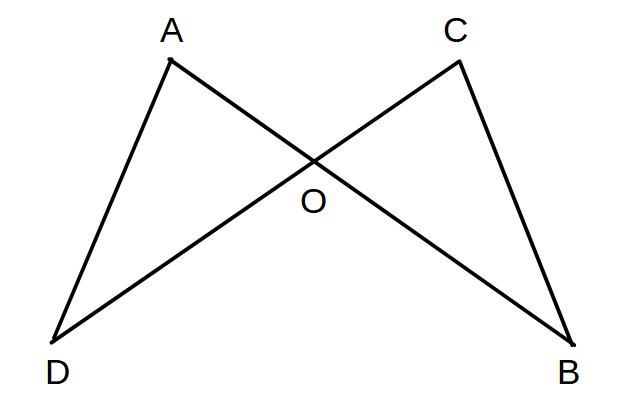
図のような図形がある。
AB=CD、AO=COのとき、
△AOD≡△COBを証明せよ。
(証明)
三角形AODと三角形CODにおいて、
仮定より、
AB=CD…①
AO=CO…②
また、
D=CD-CO…③
OB=AB-AO…④
①、②、③、④より
OD=OB…⑤
さらに、対頂角より
∠AOD=∠COB…⑥
したがって、②、⑤、⑥より、2組の辺とその挟む角が等しいので、
△AOD≡△COB
※この例2)に関しては、①と②にあるように、共通な角(辺)、大きさが等しい角(辺)の足し引きにより、等しい角や辺を証明するパターンがあるので慣れておきましょう。