今回は合同の利用、前回は単純に合同であることを証明する、というものを勉強しましたが、今回はちょっとだけひねったものです。
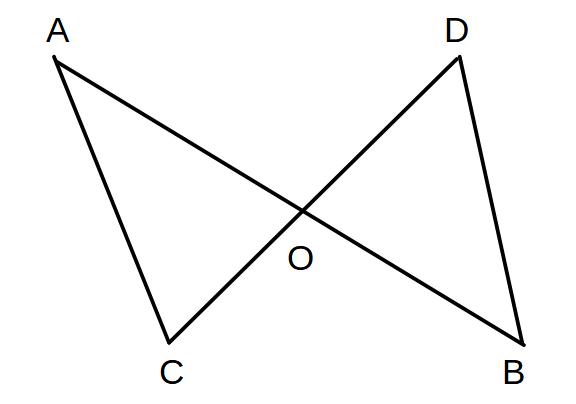
例)
AO=BO、CO=DOのとき
AC=BDであることを証明せよ
※長さや角度が等しいこと証明する問題
→証明し対辺や角度を含む合同な三角形がないかを探す
(ないときにはじめてほかの方法を考える)
→合同な2つの三角形が証明できれば、対応する辺や角は等しい
(証明)
△AOCと△BODにおいて、
仮定より
AO=BO…①
CO=DO…②
対頂角より
∠AOC=∠BOD…③
①、②、③より、2辺とその挟む角が等しいので
△AOC≡△BOD
対応する角は等しいので
AC=BD
※最後の2行を忘れない!!
※考え方として、辺や角が同じであることを証明する場合、
①まず、対応する辺や角の入った三角形を見つける
②その三角形と合同な三角形を見つける
③三角形を見つけたら、その2つの三角形が合同であることを証明する
④証明出来たら、対応する辺や角は同じ
の流れを覚えておきましょう。
くれぐれも、合同を証明して安心して終わらないようにしましょう。