
例)
直線ℓ上に点Pを置き、
AP+BPの長さを最短にするために作図し、
最短であることを証明せよ。
直線ℓについて点A(またはB)と対称な点Cを作図し、その点Cと点B(または点A)とを直線で結ぶ。この直線BC(または直線AC)と直線ℓとの交点PがAP⊥BPの最短距離になる点です(これは前の章でやりました)
作図はやっているので、ここからが今回の作図の証明になります。
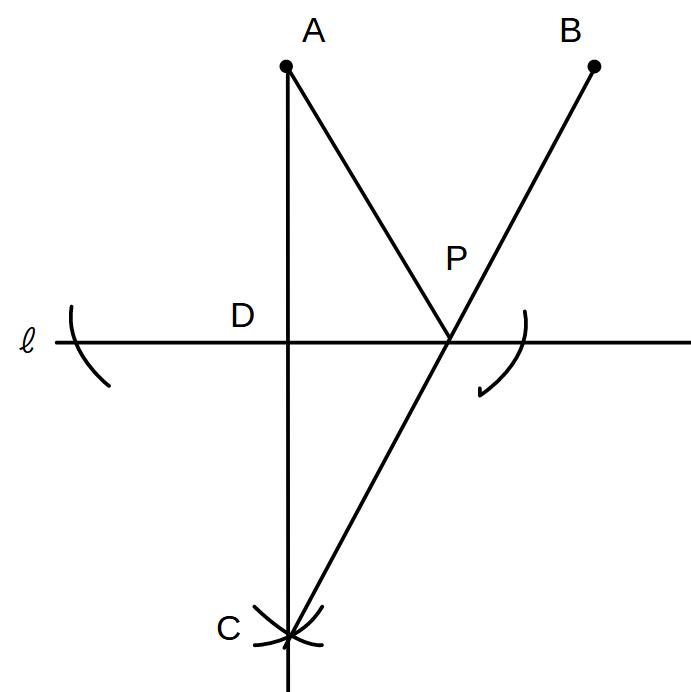
(証明)
線分ACとℓとの交点をDとする。
△ADPと△CDPにおいて、
作図より
AD=CD…①
∠ADP=∠CDP(=90°)…② ←直線ℓに垂線を引いてるから
共通な辺なので、
DP=DP…③
①、②、③より
2組の辺とその挟む角が等しいので、
△ADP≡△CDP
よって AP=CP