(1)二等辺三角形の定義
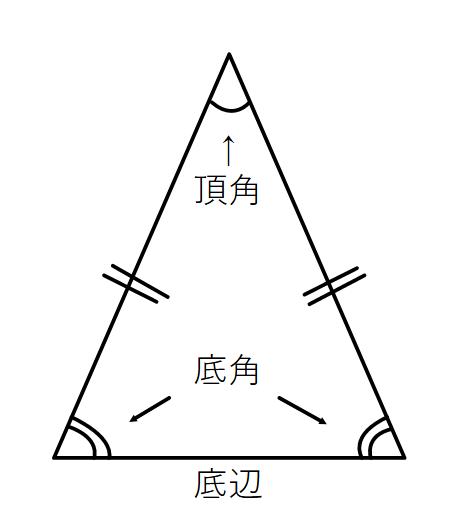
①2つの辺の長さが等しい三角形を二等辺三角形という
②二等辺三角形の等しい2辺に挟まれる角を頂角
頂角に対する辺を底辺(=頂角と向かい合う辺)
底辺の両端の角を底角という
(2)二等辺三角形の性質
①二等辺三角形の2つの底角は等しい
②二等辺三角形の頂角の二等分線は底辺を垂直に2等分する
(証明)
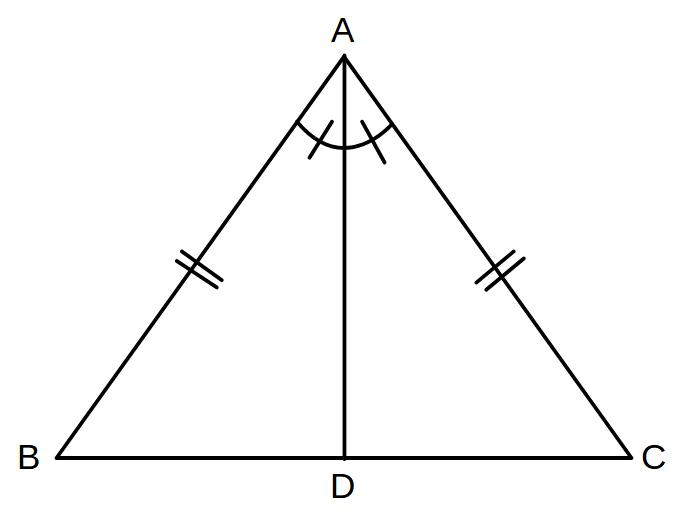
△ABCがAB=ACの二等辺三角形
(頂角である)∠BACの2等分線と
(底辺である)辺BCとの交点をDとする。
このとき、△ABDと△ACDにおいて
AB=AC(仮定)…①
∠BAD=∠CAD(仮定)…②
AD=AD(共通)…③
①、②、③より、2組の辺とその挟む角が等しいので、
△ABD≡△ACD
①ABD≡△ACDより対応する角は等しいので、∠ABD=∠ACD→定理①(底角は等しい)
②ABD≡△ACDより対応する辺は等しいので、BD=CD…①
対応する角が等しいので、∠ADB+∠ADC=180°…③
また、∠ADB=∠ADC=90°…④
①と④から、→定理②(頂角の2等分線は底辺を垂直に二等分する)
(3)二等辺三角形であるための条件

△ABCが二等辺三角形であるための条件
①2つの辺が等しい(定義)
②2つの角が等しい(定理)
AB=ACならば△ABCは二等辺三角形(→①)
∠ABC=∠ACBならば△ABCは二等辺三角形(→②)
(②の証明)
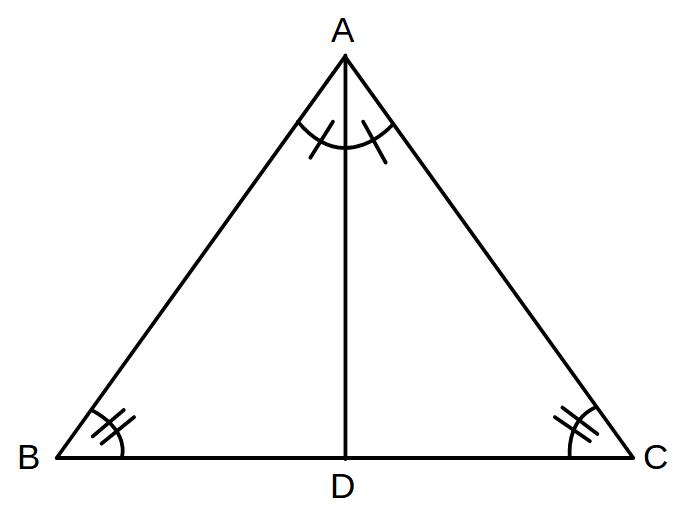
∠ABC=∠ACBのとき、AB=ACを証明する
→△ABCは二等辺三角形
∠BACの二等分線と辺BCとの交点をDとする。
△ABCと△ACDにおいて
∠ABD=∠ACD(仮定)…①
∠BAD=∠CAD(仮定)…②
①、②と三角形の内角の和が180°であることから
∠ADB=∠ADC…③
AD=AD(共通)…④
①、③、④より、1組の辺とその両端の角がそれぞれ等しいから、
△ABD≡△ACD
対応する辺が等しいので、AB=AC
よって、△ABCは二等辺三角形である。
例題)
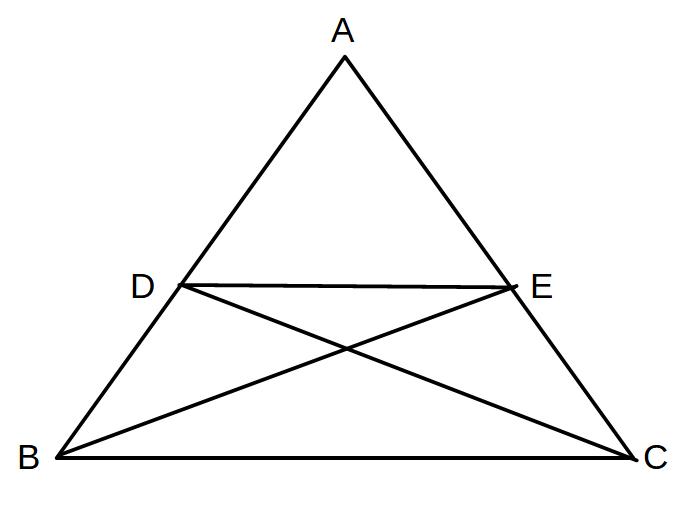
△ABCが二等辺三角形であり、BD=CEとなるような点D、EをAB、AC上にとる。
△BFCが二等辺三角形であることを証明せよ。
→条件のどちらかに当てはまればよい
→三角形の合同を利用する。
△DBCと△ECBにおいて
∠DBC=∠ECB(仮定)…①
BD=CE(仮定)…②
BC=CB(共通)…③
よって、2組の辺とその挟む角が等しいので、
△DBC≡△ECB
対応する角は等しいので
∠DCB=∠EBC
したがって、△BFCにおいて2角が等しいので
△BFCは二等辺三角形である