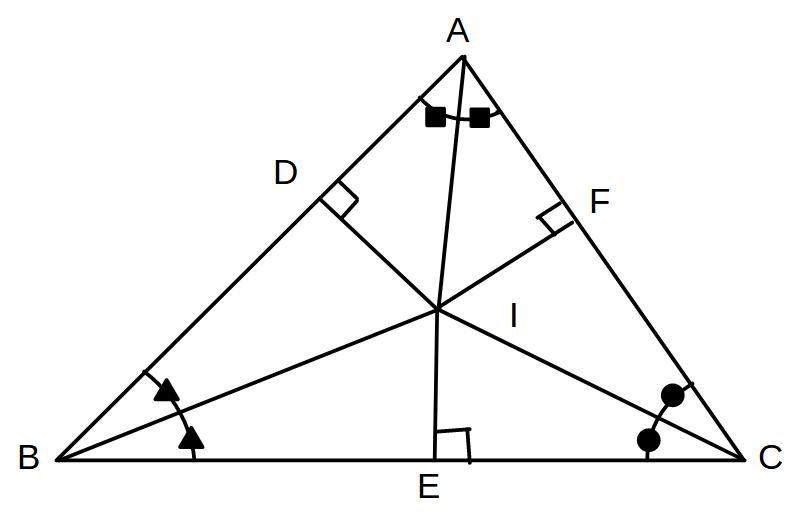
3つの内角の二等分線は1点で交わり、その点から各辺に垂線を引くと、その長さはすべて等しくなる
(→ID=IE=IF)
(証明)
△IBDと△IBEにおいて
∠IDB=∠IEB=90°(仮定)…①
∠IBD=∠IBE(仮定)…②
IB=IB(共通)…③
①、②、③より直角三角形の斜辺と1鋭角がそれぞれ等しいので
△IBD≡△IBE
対応する辺は等しいのでID=IE
つぎに
△IADと△IAFにおいて(△ICEと△ICFでもよい)
∠IDA=∠IFA=90°(仮定)…④(∠IEC=∠IFC=90°)
∠IAD=∠IAF(仮定)…⑤(∠ICE=∠ICF)
AI=AI(共通)…⑥(IC=IC)
したがって、④、⑤、⑥より
直角三角形の斜辺と1鋭角がそれぞれ等しいので
△IAD≡△IAF
対応する辺は等しいのでID=IF
よって ID=IE=IF
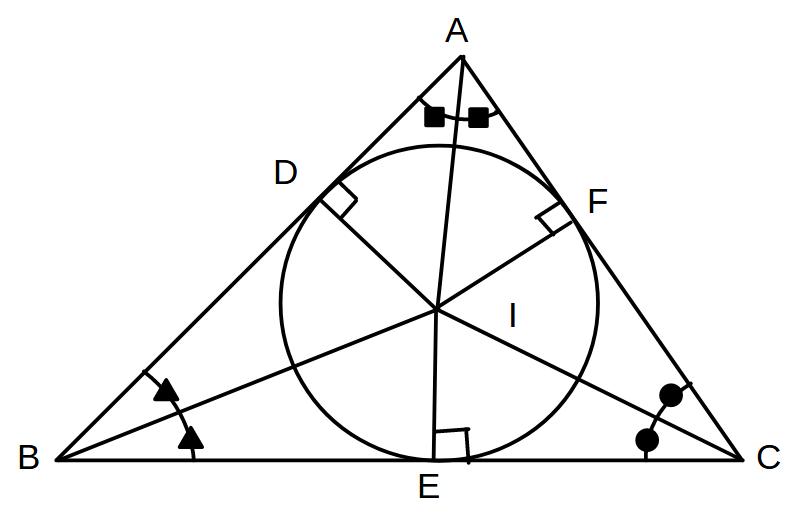
ちなみに、点Iを中心に、ID=IE=IFを半径とする△ABCの内接円ができる