(1)定義
①2組の対辺がそれぞれ平行な四角形を平行四辺形という
②四角形の向かい合う辺を対辺、向かい合う角を対角という
※平行四辺形ABCD→▱ABCDと表記
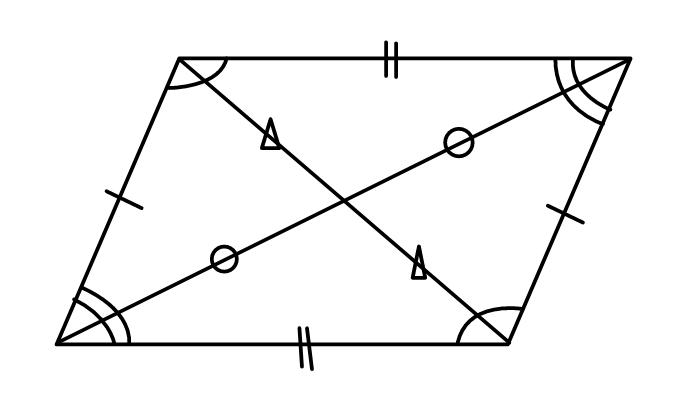
(2)平行四辺形の性質=定理
①2組の対辺はそれぞれ等しい
②2組の対角はそれぞれ等しい
③対角線はおのおのの中点で交わる
例1)
図の平行四辺形ABCDで、AB=CD、BC=ADであることを証明せよ。
(証明)
△ABCと△CDAにおいて
AB//CDより ∠BAC=∠DCA(平行線の錯角)…①
BC//ADより ∠BCA=∠DAC(平行線の錯角)…②
AC=CA(共通)…③
①、②、③より、1組の辺とその両端の角がそれぞれ等しいので
△ABC≡△CDA
対応する辺は等しいので AB=CD、BC=DA
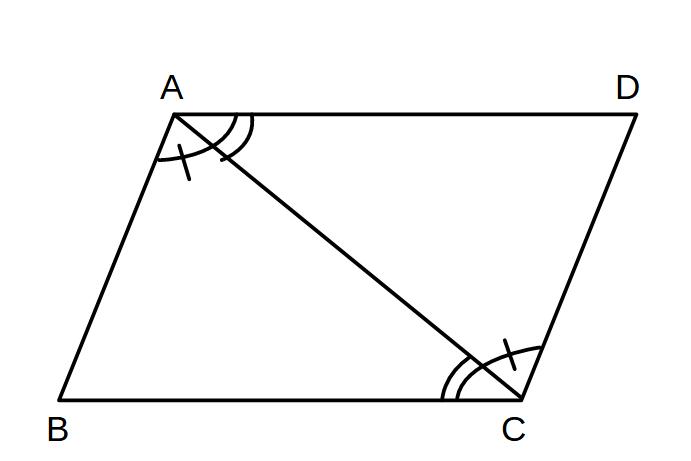
例2)
図の平行四辺形ABCDで∠A=∠C、∠B=∠Dであることを証明せよ。
(証明)AD//CDより ∠D=∠DCE(錯角)
また、AB//CDより ∠B=∠DCE(同位角)
よって∠B=∠D
同様にして∠A=∠C
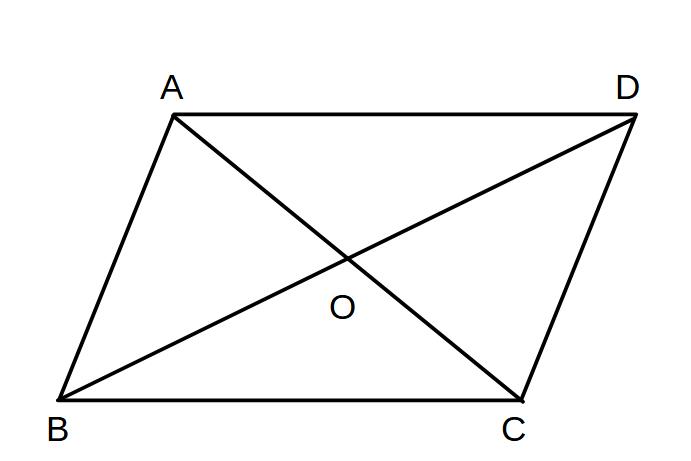
例3)
図の平行四辺形ABCDでOAOC、OB=ODであることを証明せよ。
△AOBと△CODにおいて
平行四辺形の対辺はのおのおの等しいのでAB=CD…①
AB//CDより∠ABO=∠CDO(錯角)…②
∠BAO=∠DCO(錯角)…③
①、②、③より、1組の辺とその両端の角がそれぞれ等しいので
△AOB≡△COD
対応する辺はそれぞれ等しいのでOA=OC、OB=OD
(3)平行四辺形であるための条件
①2組の対辺がそれぞれ平行である←定義
②2組の対辺がそれぞれ等しい←定理
③2組の対角がそれぞれ等しい←定理
④対角線がおのおのの中点で交わる←定理
⑤1組の対辺が平行で長さが等しい
このいずれかを使って証明する!
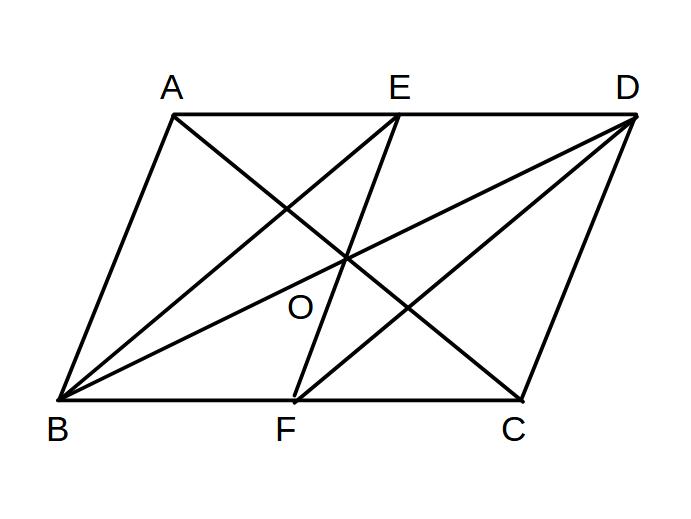
例1)
図の四角形EBFDが平行四辺形であることを証明せよ。
△BFOと△EDOにおいて
平行四辺形の対角線はおのおのの中点で交わるので、OB=OD…①
平行線の錯角より∠FBO=∠EDO…②
対頂角は等しいので∠BOF=∠DOE…③
①、②、③より、1辺とその両端の角が等しいので
△BFO≡△DEO
対応する辺は等しいのでOF=OE…④
よって①、④より対角線がおのおのの中点で交わるので
四角形EBFDは平行四辺形である
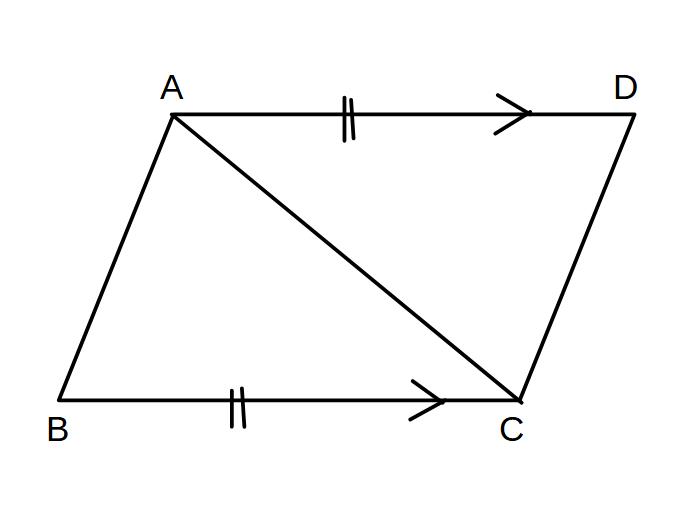
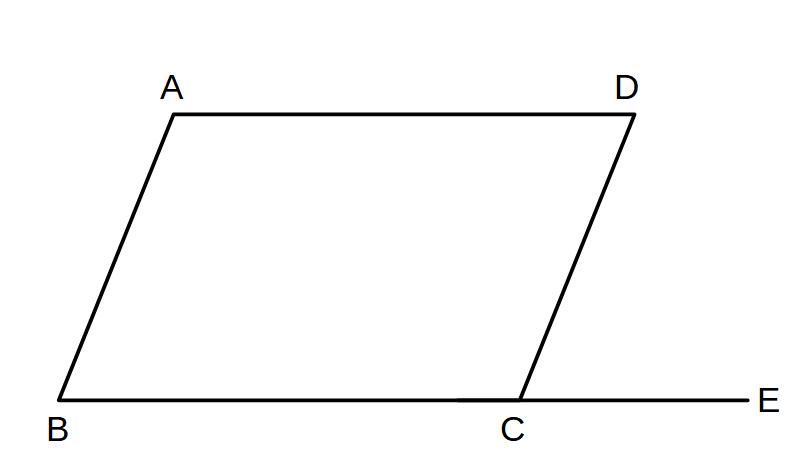
例2)
図の四角形ABCDにおいて
AD//BC、AD=BCのとき
四角形ABCDが平行四辺形であることを証明せよ。
△ABCと△CDAにおいて
仮定より
BC=DA…①
またAD//BCより
∠BCA=∠DAC(錯角)…②
AC=CA(共通)…③
①、②、③より、2組の辺とその挟む角が等しいので
△ABC≡△CDA
対応する角は等しいの
∠BAC=∠DCA
∠BAC、∠DCAは2つの直線AB、CDの錯角であるから
錯角が等しいのでAB//CD
よってAB//CD、AD//BCなので、四角形ABCDは平行四辺形である
(4)平行四辺形の面積を2等分する直線
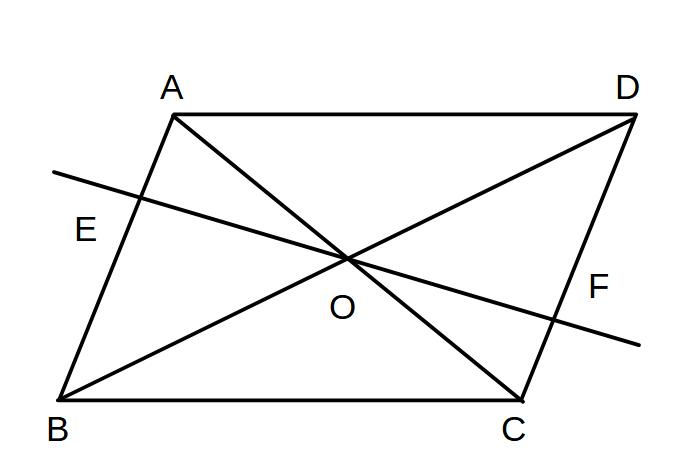
対角線の交点を通る直線は
平行四辺形の面積を2等分する
※このとき、EO=FOである
点Oは対称の中心
(5)特別な平行四辺形
①長方形…4つの角が等しい四角形
②ひし形…4つの辺が等しい四角形
③正方形…4つの角が等しく、4つの辺が等しい四角形
→これらは、平行四辺形の特別なもの
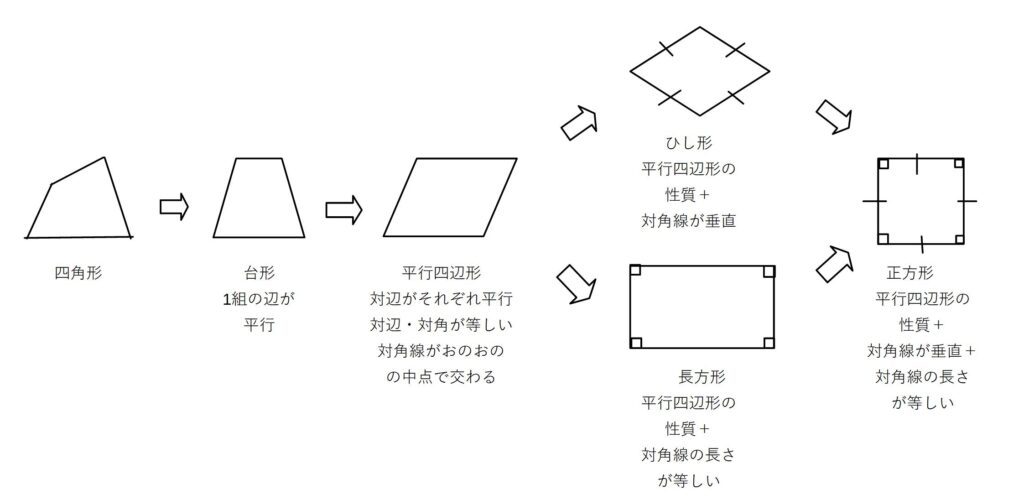
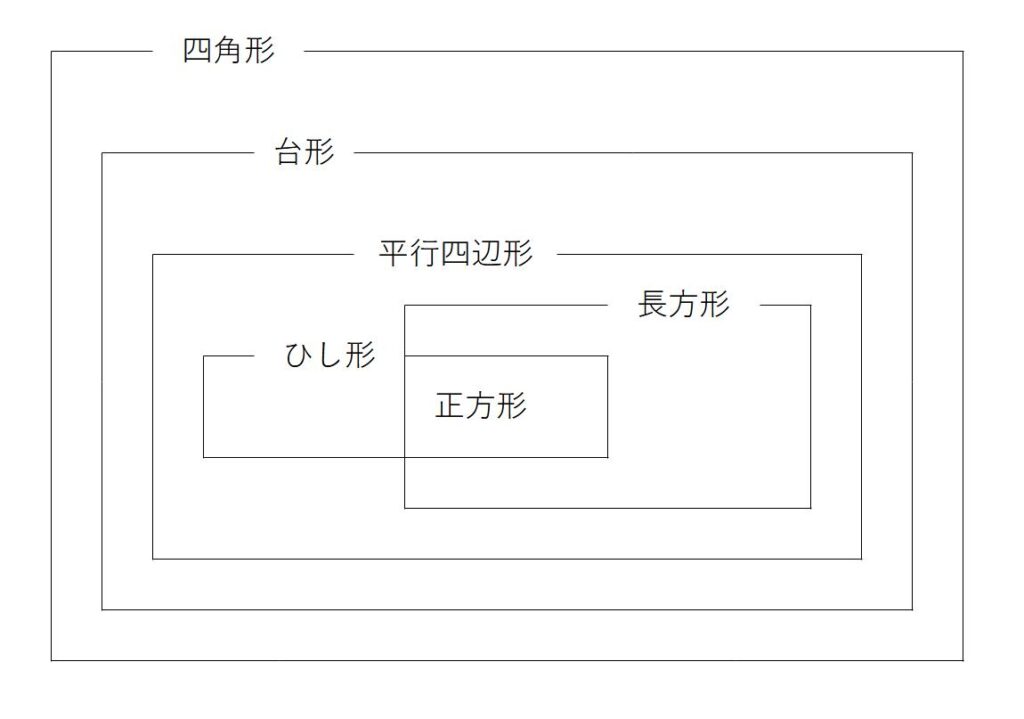
ひし形・長方形・正方形は、平行四辺形の特別な形なので、平行四辺形の性質は当然に持っている
→対角線の交点で面積は二等分される
ひし形正方形の面積
(対角線)×(対角線)×1/2
※補足 台形の二等分

①上底の中点と下底の中点を結ぶ
②①の線分の中点を取る
③②の点を通り、かつ、上底と下底に交わる直線であれば、台形を二等分している線が引ける!