今回の円周角の定理は、きちんと覚えてしまうのが大前提と考えてください。
定理を使って、問題を解けるようになってください。
(1)円周角と中心角
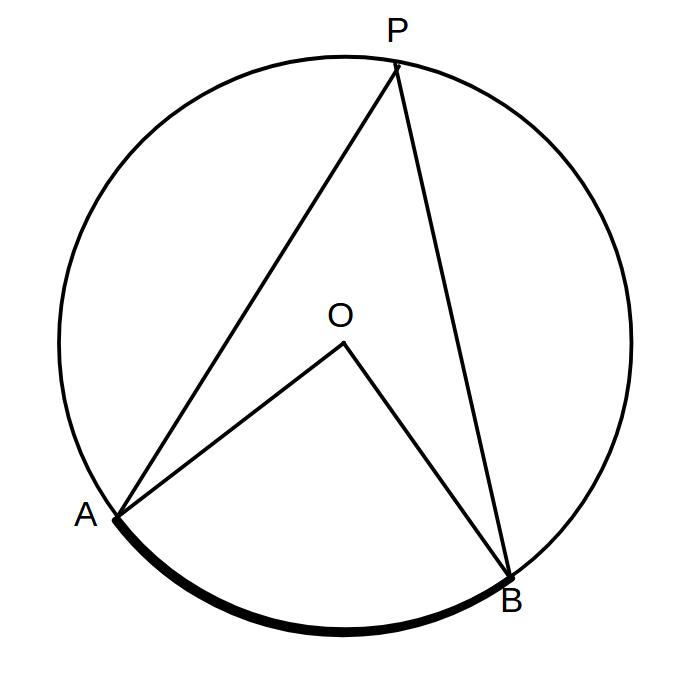
※円Oにおいて弧ABを除いた演習上に点Pを取るとき
①∠APBを弧ABに対する円周角という
②弧ABを円周角∠APBに対する弧という
③また、このとき∠ACBを弧ABの中心角という
(2)円周角の定理と中心角・弧との関係
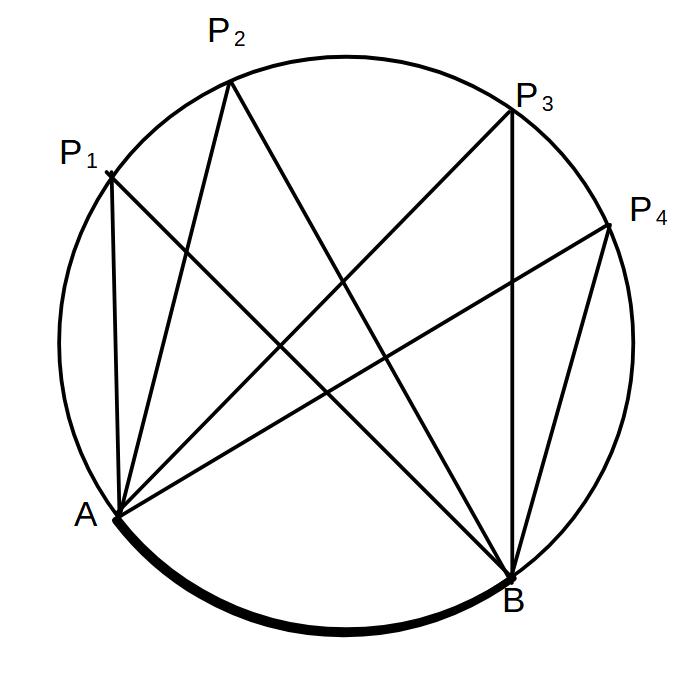
①∠AP₁B=∠AP₂B=∠AP₃B=∠AP₄B
円周角の定理
→同じ弧に対する円周角の大きさはすべて等しい
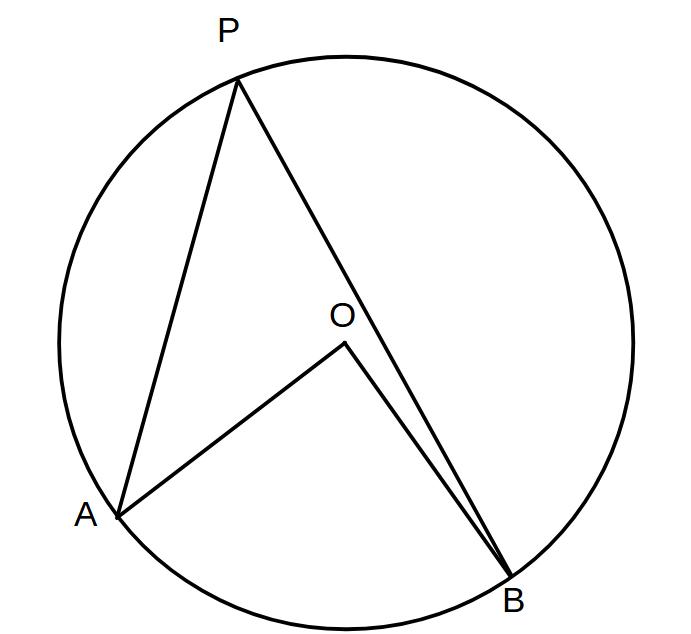
②∠APB=50°のとき ∠AOB=100°
また
∠AOB=110°のとき∠APB=55°
→1つの弧に対する円周角の大きさは、その弧に対する中心角の半分
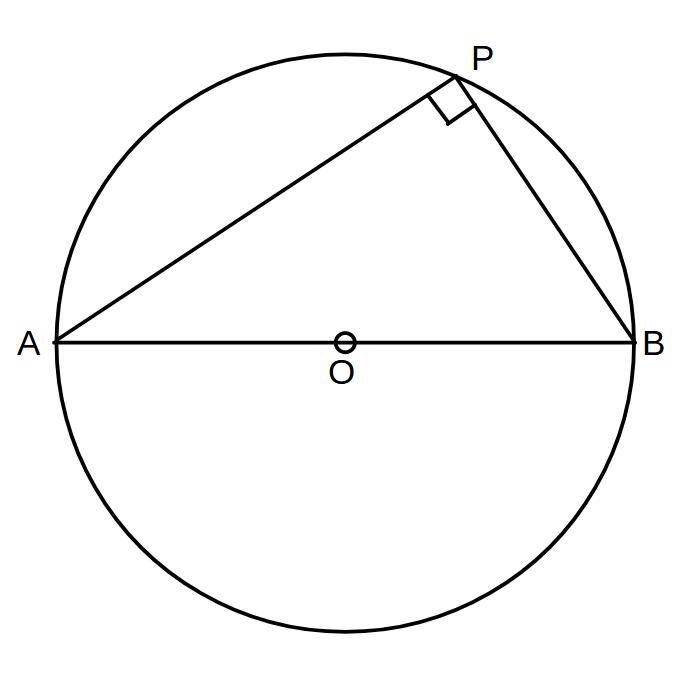
③ABが円Oの直径のとき
∠APB=90
線分ABが円の直径のときの弧ABに対する円周角は90°
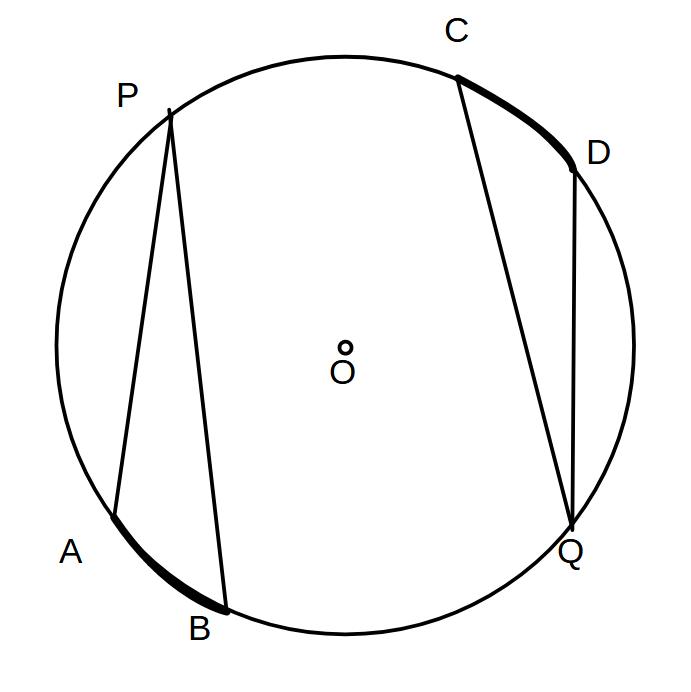
④弧AB=弧CDのとき
∠APB=∠CQD
⑤∠APB=∠CQDの時
弧AB=弧CD
1つの円で長さの等しい弧に対する円周角は等しい
1つの円で円周角の大きさが等しいならば、その円周角に対する弧は等しい
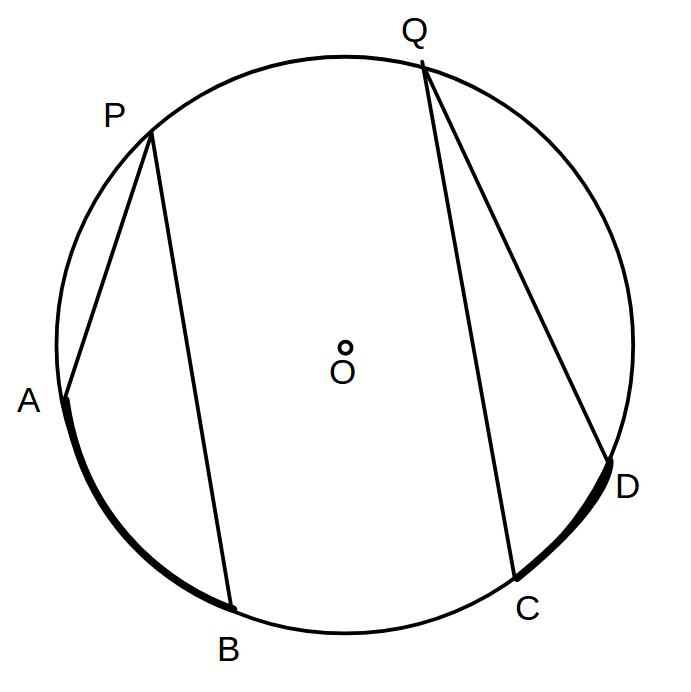
⑤∠APB=30°
弧AB:弧CD=3:2のとき
∠CQD=20°
また∠APB=30°、∠CQD=20°のとき
AB:CD=30:20=3:2
1つの円で弧の長さは円周角の大きさに比例する
=弧の長さの比と円周角の比は等しい
(3)円周角の定理の逆
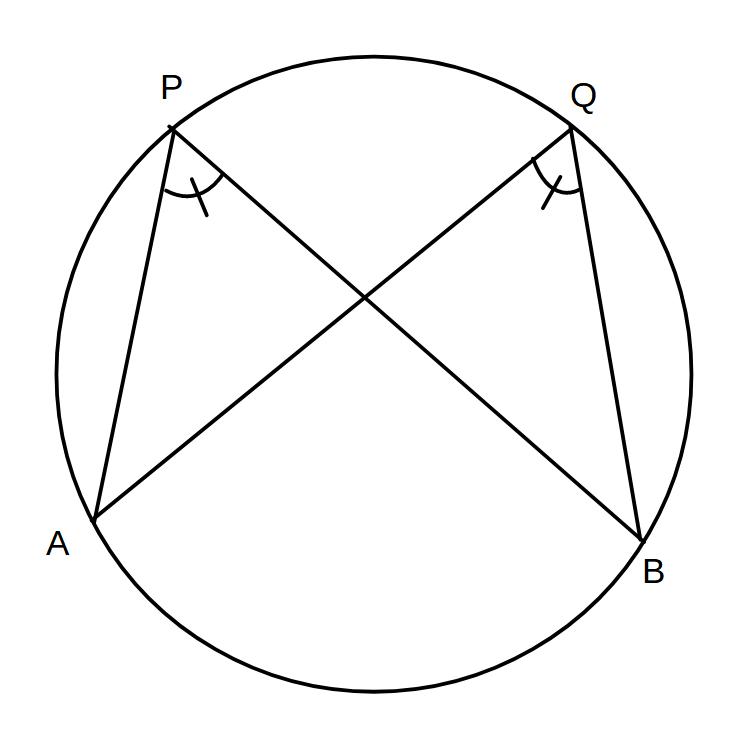
※2点P、Qが線分ABに対し同じ側にあって、∠APB=∠AOBのとき、4点A、B、P、Qは1つの円周上にある
∠APB=∠AOBがABの円周角になる