※接弦定理
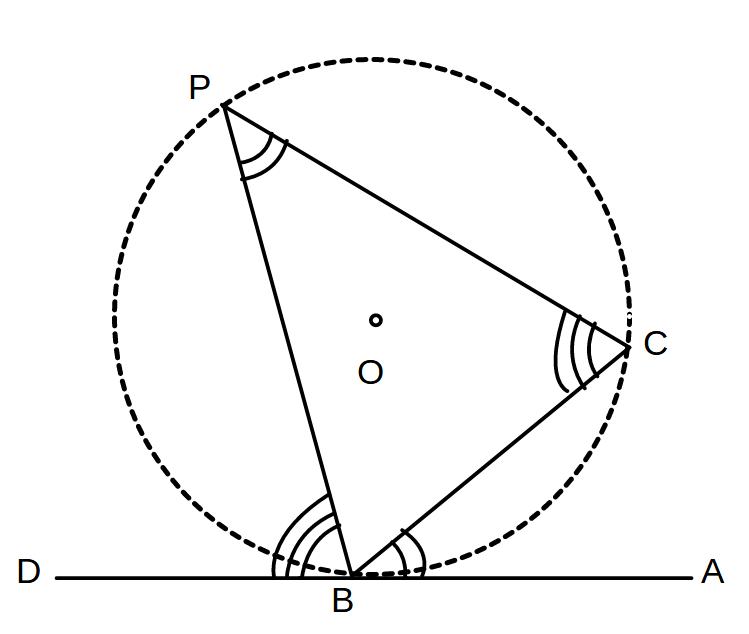
円の弦とその一端を接点とする円の接線とがつくる角はその角内の弧(=弦の両端の弧)に対する円周角に等しい
∠ABC=∠BPC
∠PBD=∠PCBもある
※あくまで、弦と接線が作る角がその弦を両端とする弧がつくる円周角と等しい、ということに注意しましょう。
→∠BPCが∠ABCと等しいのであり、∠BCPではないことに注意
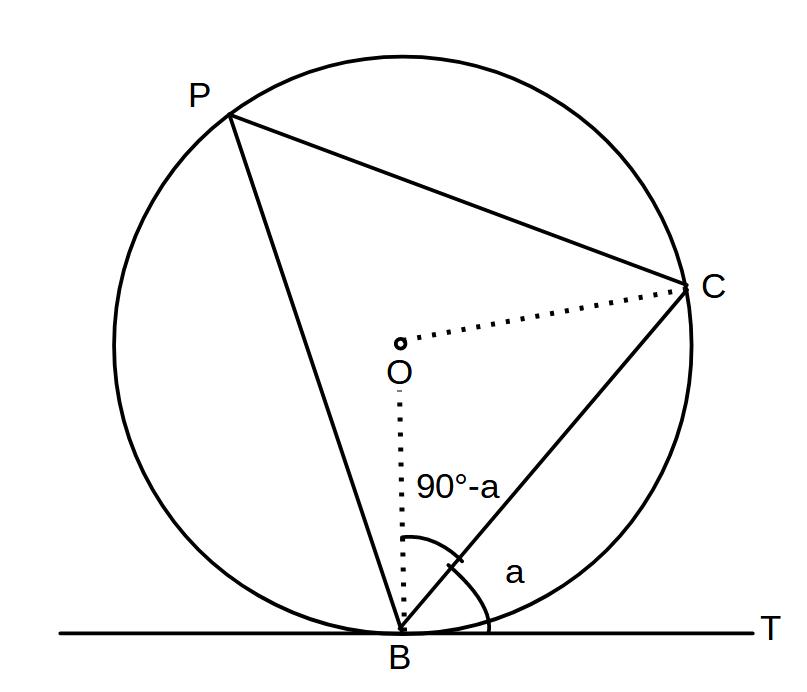
接弦定理の理由
∠CBT=aとおくと
∠OBT=90° より
∠OBC=90°ーa
△OBCは二等辺三角形より
∠OCB=90°ーa
よって
∠BOC=180-2(90-a)
=2a
これより∠BPC=a
よって、∠BPC=∠CBT