あることがらの起こり方が全部で何通りあるか
→樹形図、表などを使ってきちんと数える
例1)1,2,3,0が書いてあるカードが1マスずつある。その中から3枚を抜き出してできる3桁の数は何通りになるか。
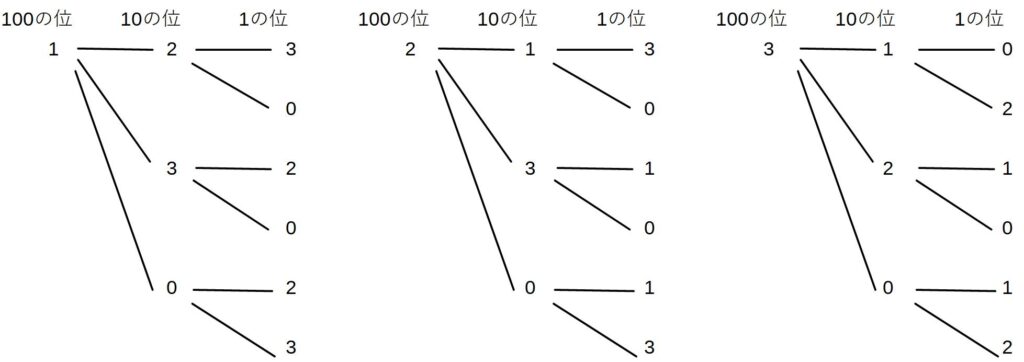
※基本は樹形図を書く!
枝分かれをはっきり書いて、漏れや重複がないようにする
→図よりそれぞれの数を数えると
6×3=18(通り)
例2)100円玉、50円玉、10円玉、1円玉の中から2枚を選ぶとき、選び方は何通りあるか。
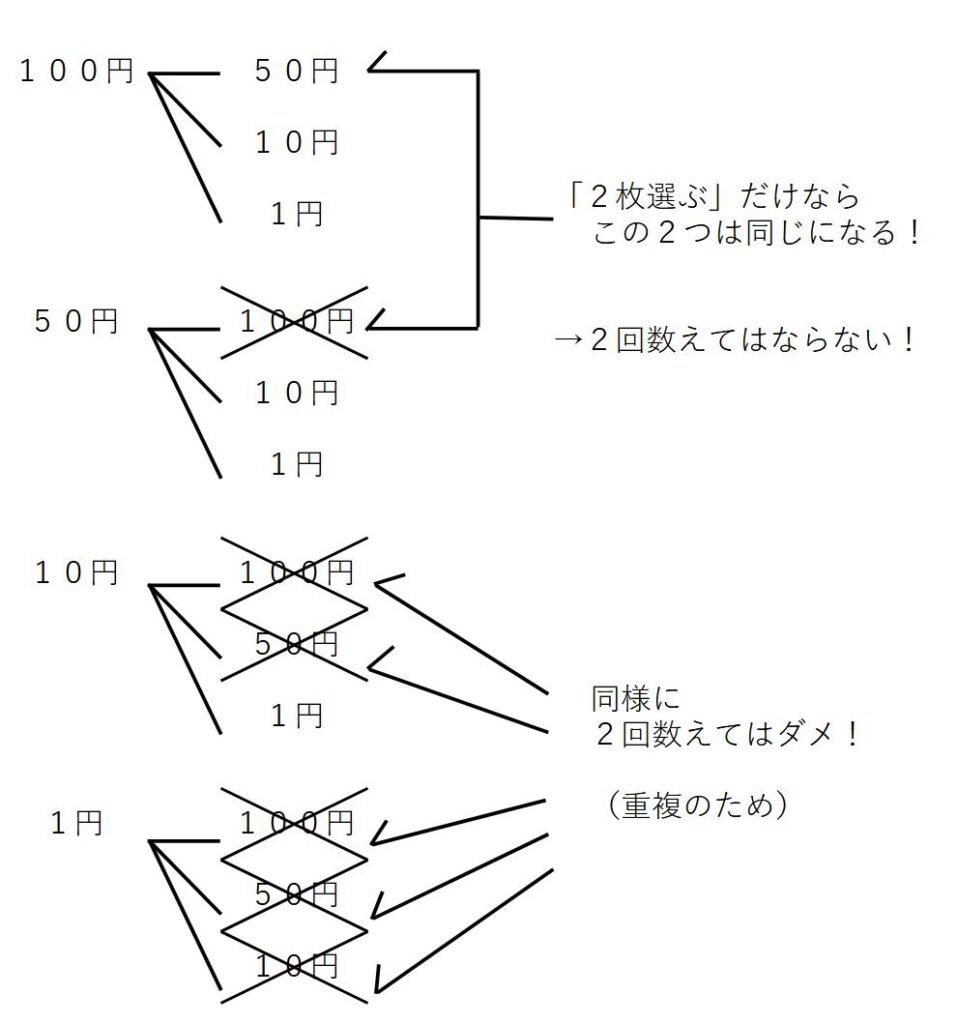
例2)の問題は例1)の問題と明らかに違う点があります。
例1)の場合は、とりあえずすべての場合を取り上げれば解答できたのですが、例2)の場合はちょっと様子が変わります。
例えば、例1)はA→Bの場合とB→Aの場合は違うのに対し、例2)はA→BとB→Aの並びの場合が同じことになってしまいます。
つまり、例2)は例1)と違って重複が存在するのです。
実際、重複を取り除いた場合が図のようになり、全部で6通りとなります。
つまり、A→B、B→Aの2つが
①順番が必要なとき→2通り
②順番が関係ないとき→1通り
と数えまず
①のときは枝の数が減らない樹形図になり、
②のときは枝の数が減っていく樹形図になります。

↑②の場合の樹形図の形