(1)サイコロ
例1)サイコロの1の目が出る確率は
目が6個のうちの1つなので、1/6
1~6まで出る確率はどれも同じ
=「同様に確からしい」という
例2)サイコロを2個投げて、出た目の和が8以上になる確率
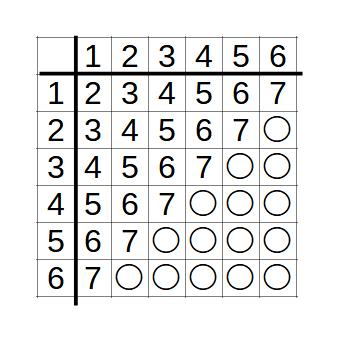
表を書いてみる
全部で36通りある
その中で、和が8以上の場合は15通り
よって、5/12になる
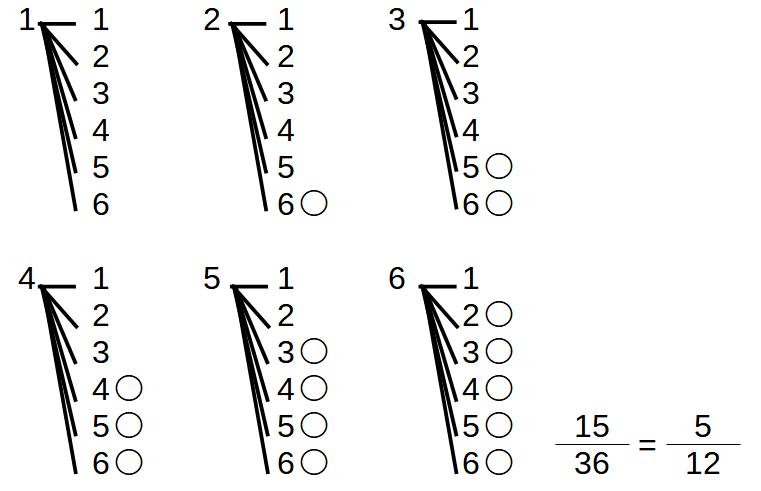
ちなみに、この場合は表を使った方がうまくできる。
基本的には樹形図を書いて解いていくのがよいが、サイコロを2個ふるパターンの問題等では表の方がわかりやすい場合がある。
いずれにせよ、すべての場合とそうなる場合の数を正確に数える方法をしっかり身につけて、活用できるようになってください。
(2)カード
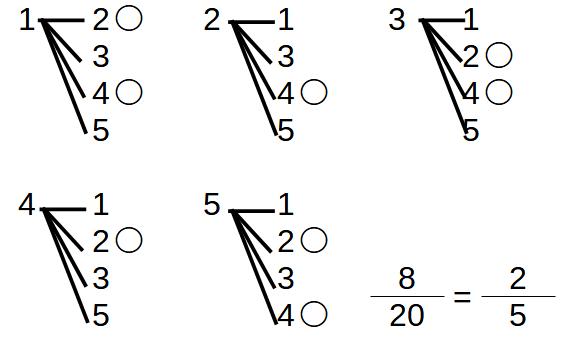
例)1~5までの数字が書いてある5枚のカードがある。このカードのうち、2枚並べてできる2桁の整数を作るとき、偶数である確率を求めよ。
この場合は、A→BとB→Aが別の意味になるので全て数えるパターンです。
数えると全部で20通り
偶数は8通り
確率は2/5になります。
(3)コイン
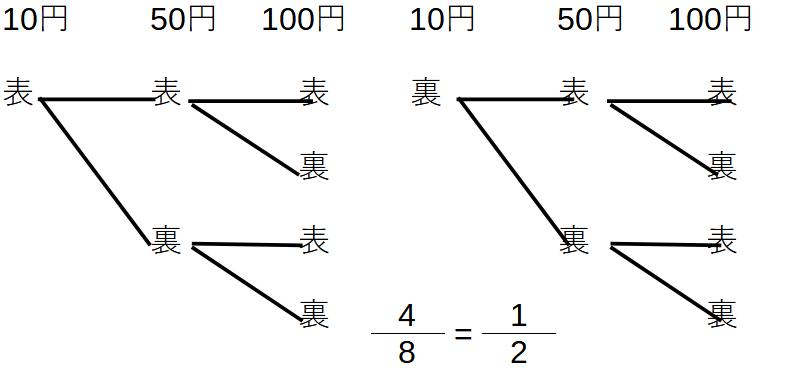
例1)10円、50円、100円を同時に投げて、2枚以上表が出る確率は?
3枚のコインを同時に投げて…という問題なので、自分で3つのコインを区別します。(貨幣単位などで区別できなかったら、自分でA,B,Cなどと分けます)
今回は単位があるので、それで分けます。
全部で8通り
表が2枚以上=4通り
よって、確率は1/2
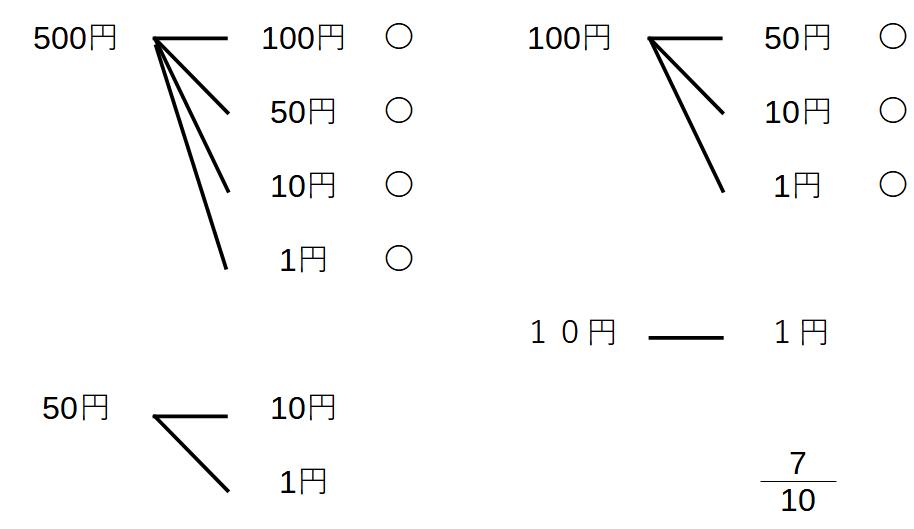
例2)500円、100円、50円、10円、1円から2枚選んで合計100円以上になる確率は?
この場合、500円→100円と100円→500円は順番が関係ないので同じになる
→枝の数が減っていく樹形図を書く!
全部で10通り
100円以上は7通り
確率は7/10
(4)玉を選ぶ
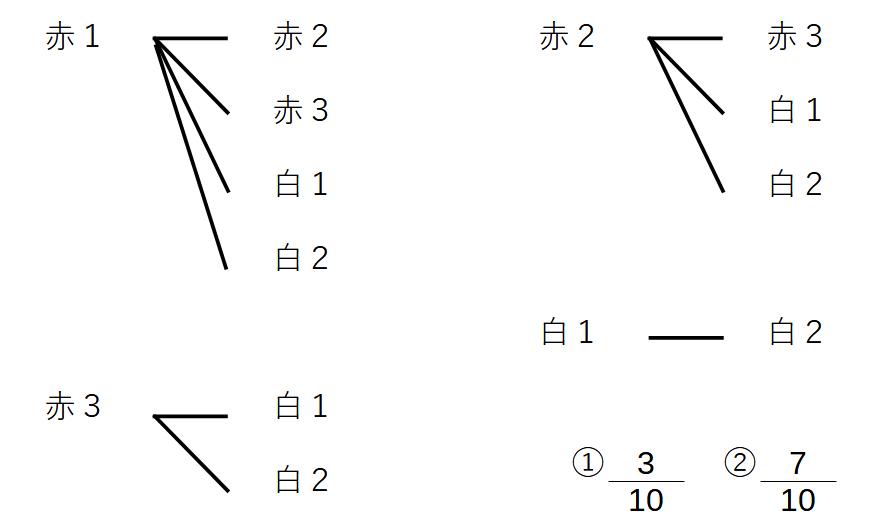
例)赤玉3つ、白玉2つが入っている袋がある。そこから同時に2個取り出すとき
①2個とも赤玉の確立
②少なくとも1個は白玉である確率
を求めよ。
※同じ赤玉でも、複数あるので、別の赤玉を取り出すことには違いがある
→番号を打って同じ色の球を区別する!
※順番は関係ないパターンなので、枝の数は減っていく樹形図を使用する。
①全部で10通り
2個とも赤玉=3通り
確率は3/10
②少なくとも1個は白玉
→白玉は1個でも2個でもいい
全部で10通り
白玉1、あるいは白玉2個=7通り
確率は7/10
(5)くじ引き
例)5本中3本のあたりくじが入っているくじがある。
くじを2本同時に引くとき、1本だけ当たりの出る確率は?
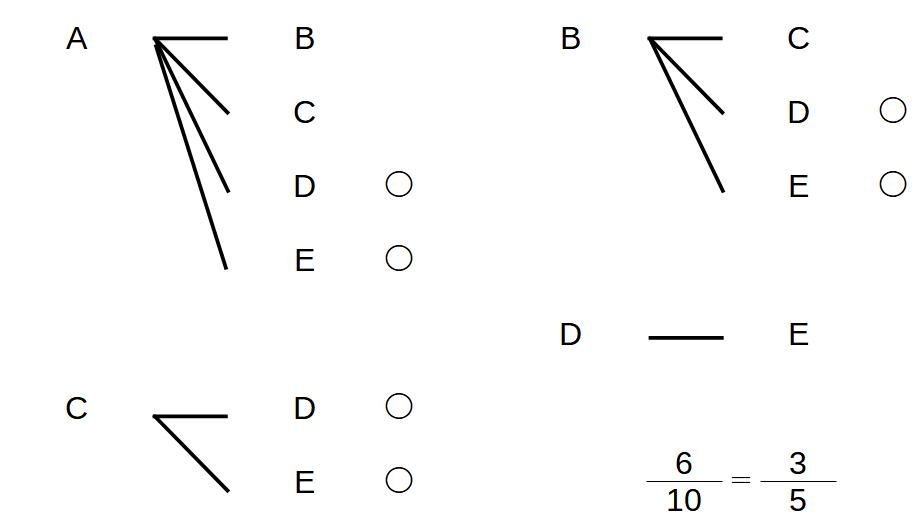
※くじをABCDE(12345でもよい)と区別して、先に当たりくじを決める!
※2本同時なので、くじの順番は関係ない
→枝が減っていく樹形図を使用
今回は、DとEをあたりとして考える
全部で10通り
1本だけ当たり=6通り
確率は3/5
(6)まとめ~確率を解く流れ~
①同じ種類・同じ色など、一目で区別できないもの
→番号・記号などで自分で区別する!
②①をもとに樹形図を書く
→枝が減るか減らないかを、問題文から判断する(←慣れるまで結構難しいので、頑張りましょう)
③作った樹形図から、そうなる場合/すべての場合 を正確に数える
※最後に約分できるときは必ずすること!!