(1)数
①2つの正の整数があり、和は17、積は60である。大きいほうの整数を求めよ。
2つの数をx、yとおく。
x+y=17―①
xy=60―② 連立!
① x=17-y
②に代入 y(17-y)=60
17y-y2=60
y2-17y―60=0
(y-12)(y-5)=0
y=5、12
②連続した2つの正の整数があり、それぞれの平方の和は85
になる。2つの整数を求めよ。
※整数の表し方、おさらいです。

連続する2数…n、n+1 とおく
平方の和 …n2+(n+1)2
n2+(n+1)2=85
n2+n2+2n+1=85
2n2+2n-84=0
n2+n-42=0
(n-6)(n+7)=0
n=6、-7
ー7は正でないので×
n=6
n+1=7 A.6,7
(2)割合
原価1500円の品物にx%の利益を見込んでつけた定価から
x%を割引したら、原価より60円安くなった。定価を求めよ。
※例によって、割合の表し方、おさらいです。

※価格とその言葉の意味(覚えておくとよいです)
原価 ものを作る(仕入れる)のにかかった値段です。
↓+利益(見込) 儲けです
定価 本来売りたい値段です
↓一割引
売り値 売り場に出てる時の値段です
実利益=売り値-原価
ものを打った時の値段から、ものを作った(仕入れた)時の値段を引くと、もうけが出ます。
それを前提として、問題文の通り文字式を作ってみましょう。
原 1500 実利益 -60円
↓ x%増
定 1500(1+ x/100) ←原価のx%です
↓ x%引
売 1500(1+ x/100)(1- x/100) ←原価のx%のx%割引です
-60=1500(1+ x/100)(1- x/100)-1500
実利益 売り値 原価
これで、問題文通りの文字式が完成しました。2次方程式です。
これを計算していきます。
1440=1500(1- x2/10000)
1440=1- x²
1500 10000
60 = x²
1500 10000
460×10000=x2
1500
x2=400 x=20
x=±20 定価 1800円
(3)動点
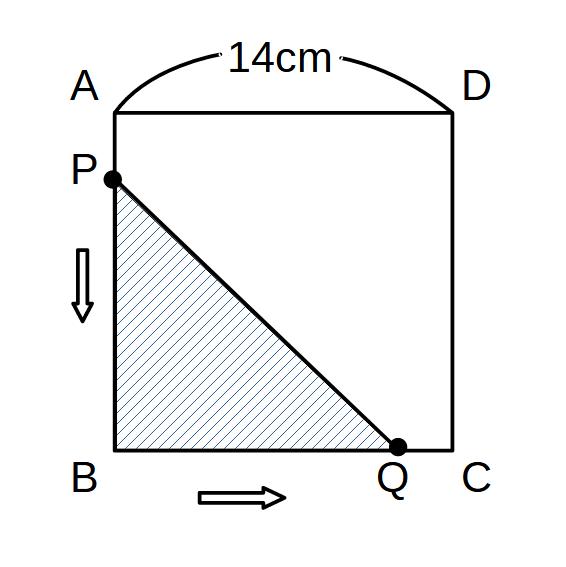
例1)
1辺14cmの正方形ABCD上を、点PはA~B、点QはB~Cまで毎秒1cmの速さで動く。
P、Qが同時に出発すると△PBQ=12c㎡になるのは何秒後か。
※動点のポイント
①出発してからの時間をxとおく。
②動点の動いた道のりをxで表す。
(みはじで計算)
③残った長さもxで表す。
解)
時間…x秒とおく。
AP(Pの道のり)=1×x=x
(速さ×時間)
BQ(Qの道のり)=1×x=x
PB=1辺-AP
=14-x
△PBQ=BQ×PB× 1/2
=(14-x)× x × 1/2
=1/2 x(14-x)
△PBQ=12になるのは、1/2 x(14-x)=12
x(14-x)=24
14x-x2=24
x2-14x+24=0
(x-12)(x-2)=0
x=2、12 2秒後、12秒後
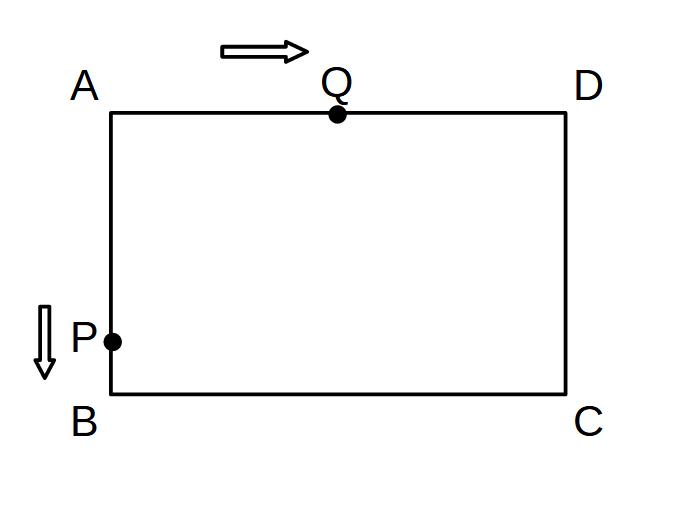
例2)
たて4cm、よこ8cmの長方形上を、点PはA~B~C~Dを毎秒2cmで、点QはA~Dを毎秒1cmで動く。
(1)2秒~6秒の間で、△APQ=8となるのは何秒の時か。
(2)6秒~8秒の間で、△APQ=7となるのは何秒の時か。
※点が曲がる→図形が変化する

(1)時間x秒とすると、
AQ=x
\( \displaystyle △APQ=x \times 4 \times \frac{1}{2}=8 \)
2x=8
x=4 4秒
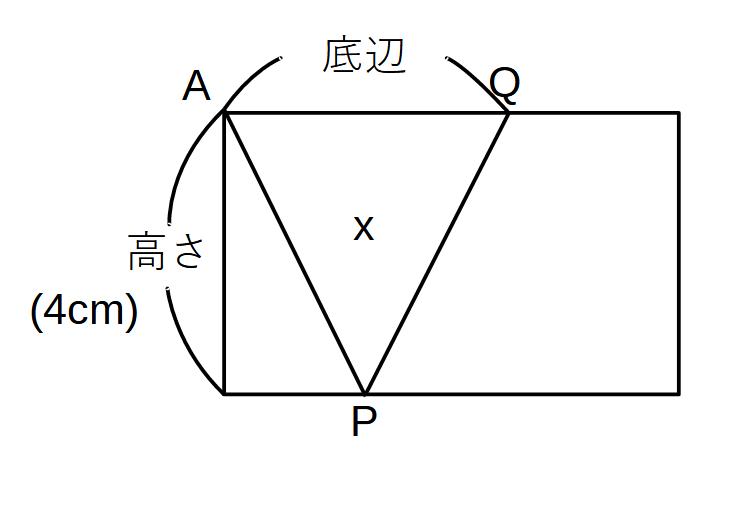
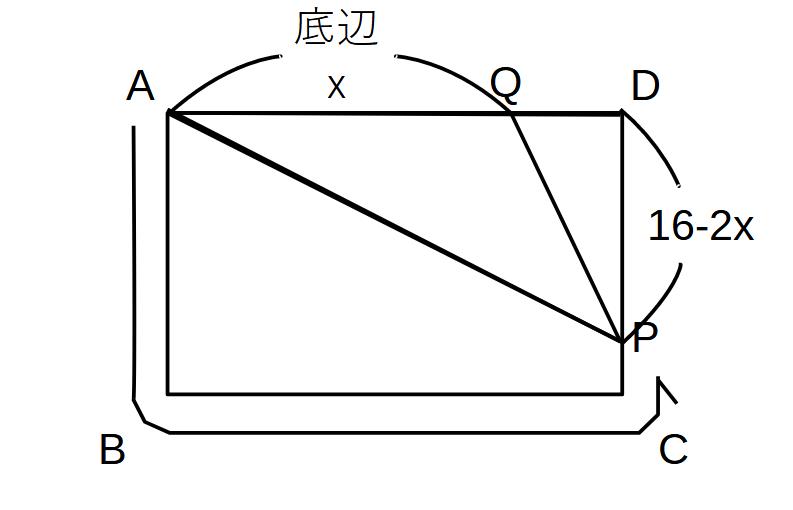
(2)
AQ=x DP=16-2x
\( \displaystyle △APQ=x(16-2x) \times \frac{1}{2}=7 \)
16x-2x2=14
-2x2+16x-14=0
x2-8x+7=0
(x-1)(x-7)=0
x=1、7 ※1は6~8でないので× ∴7秒
(4)立体の組み立て
例)
横がたてより4cm長い長方形の四すみから1辺3cmの正方形を切りとり、容積180cm3の容器を作った。もとのたて・よこの長さを求めよ。

たて…x cmとおく
よこ…x+4 (cm)
容器のたて…x-6(cm)
よこ…x-2(cm)
高さ…3 cm
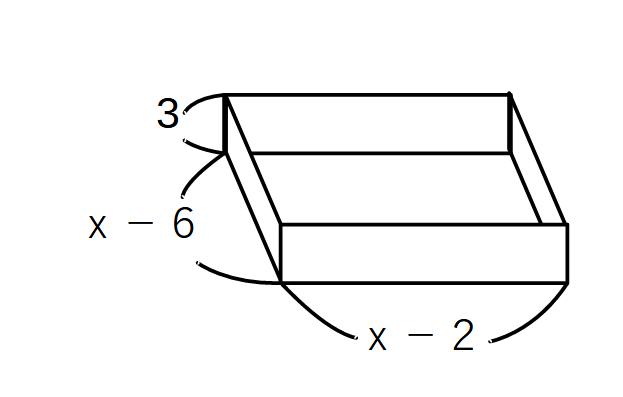
容積
(x-6)(x-2)×3=180
(x-6)(x-2)=60
x2-8x+12=60
x2-8x-48=0
(x-12)(x+4)=0
x=12、-4 ※ー4は×
たて 12cm、よこ 16cm