2次関数の変域についてです。
やはり、今までとはちょっと違うみたいですので、今までの復習をしてから、違いを見ていきましょう。
変域とは…とりうる値の範囲
xの変域…定義域といい、
yの変域…値域といいます。

1次関数の場合の変域の求め方
a<x<bのとき、
c<y<d
(a,c)でxもyも最小
(b,d)でxもyも最大
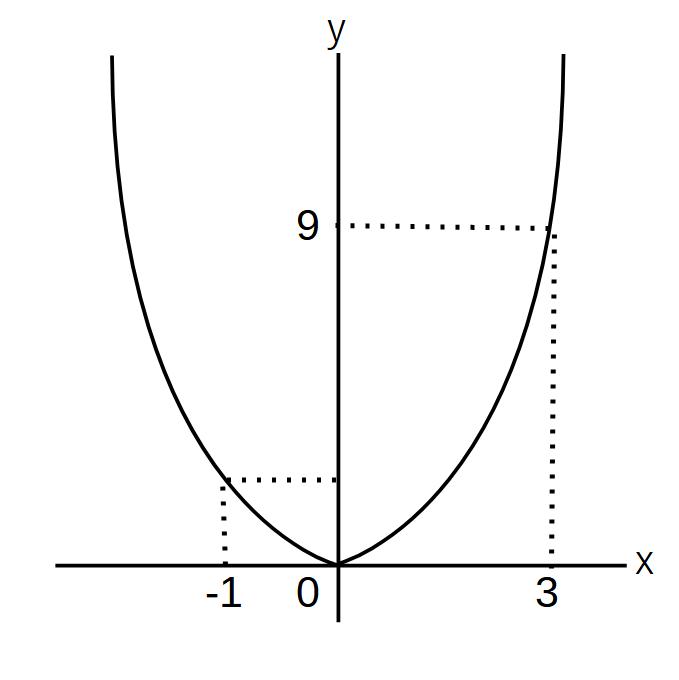
y=x2において、xの変域(-1≦x≦3)のとき、yの変域
xはx=-1で最小
yはx=0で最小
→一致しない!
なので、変域はグラフで考える!
グラフを見ていくと、
0≦y≦9 となる
① y=3x2で(-2≦x≦2)のときのyの変域
0≦y≦12
② y=1/2 x2で(2≦x≦4)のときのy
2≦y≦8
③ y=-4x2で(-1≦x≦3)のときのy
-36≦y≦0
※これらも、グラフをみて答える