等積変形を使った問題の解法です。
まず、等積変形とは何かおさらいです。
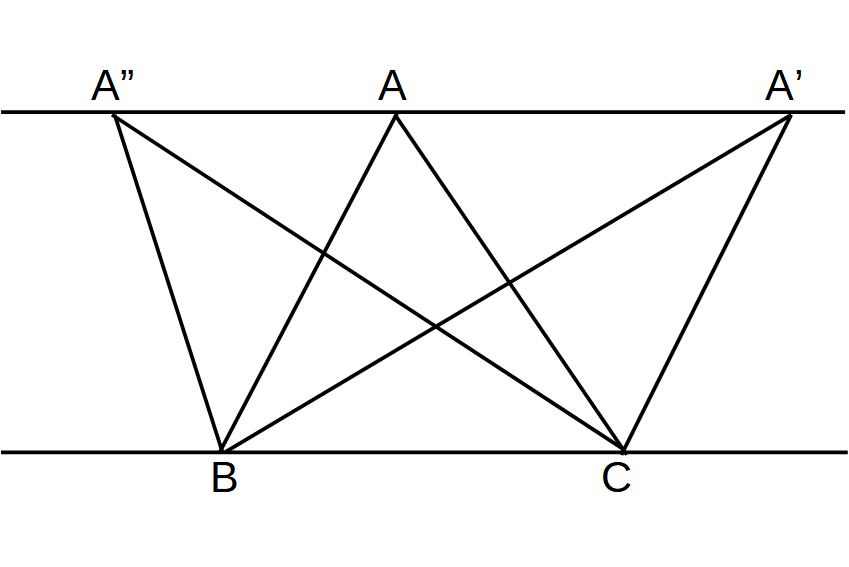
三角形の頂点は、底辺に平行な直線上を等しい面積のまま動かせる。
△ABC=△A´BC=△A″BC
※底辺BCは同じ長さ、高さも同じ
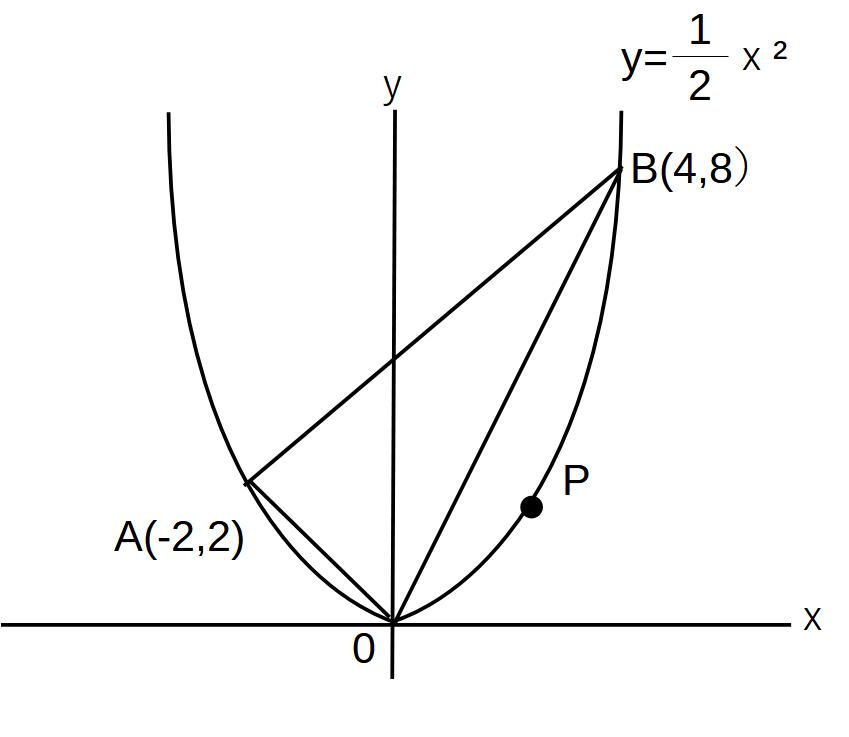
例)
y=1/2x2上に点ABを取り、そのA~B間に直線を引き、原点Oとつないだ△OABと、底辺を線分ABと、y=1/2x²上にある点Pを結んだ△PABが同じ面積になるとき、点Pの座標を求めよ。
y=1/2x2のA~B間にあり
△AOB=△APBになる点P
△AOBと△APBはAB共通
→ABを底辺としてOを動かす!
ABと平行でOを通る線lをひく。
ℓ:y=x
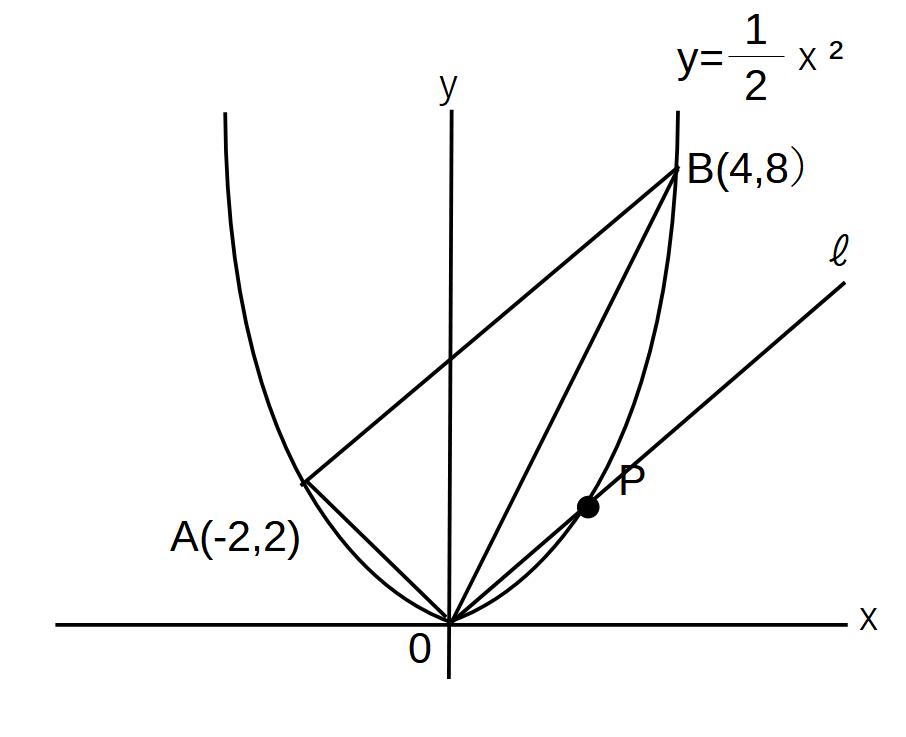
Pはy=1/2x2とlとの交点
y=1/2x2
y=x
1/2x2=x
1/2x2-x=0
x(1/2x-1)=0
x=0、2
点Oなので×
Pのx=2
P(2,2)
※①平行な直線の式を立てる
②連立で点を求める
の順で進めていく!