(1)相似
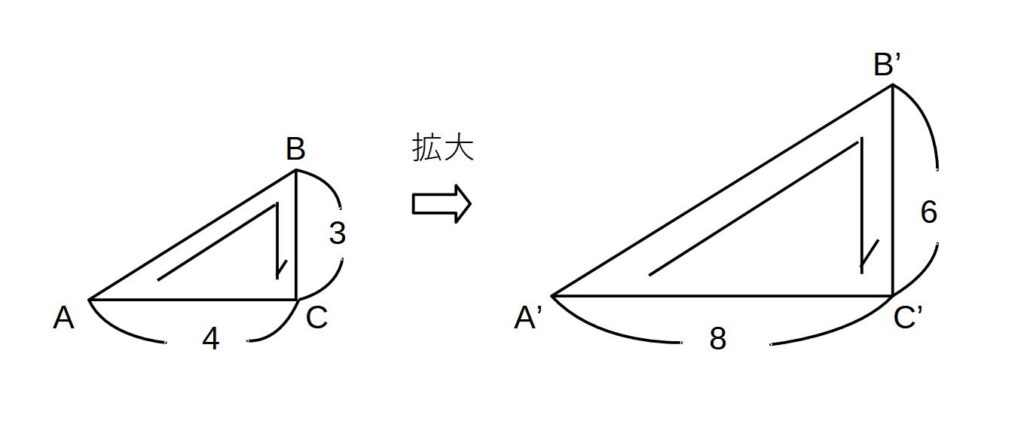
△ABCと△A′B′C′は大きさは違うが形は同じ
→△ABCと△A′B′C′は相似である
△ABC∽△A′B′C′
∽:相似であるという記号
辺ABと辺A′B′
辺BCと辺B′C′
辺CAと辺C′A′ の3つを対応する辺という
∠Aと∠A′
∠Bと∠B′
∠Cと∠C′ の3つをの対応する角という
(特徴)①AB:A′B′=BC:B′C′
5 : 10 = 3 : 6
1 : 2 = 1 : 2
対応する辺の比は同じ
→△ABCと△A′B′C′の相似比という。
②AB:BC=A′B′:B′C′
5 : 3 = 10 : 6
5 : 3
2辺の比は同じ
→矢印でとる!
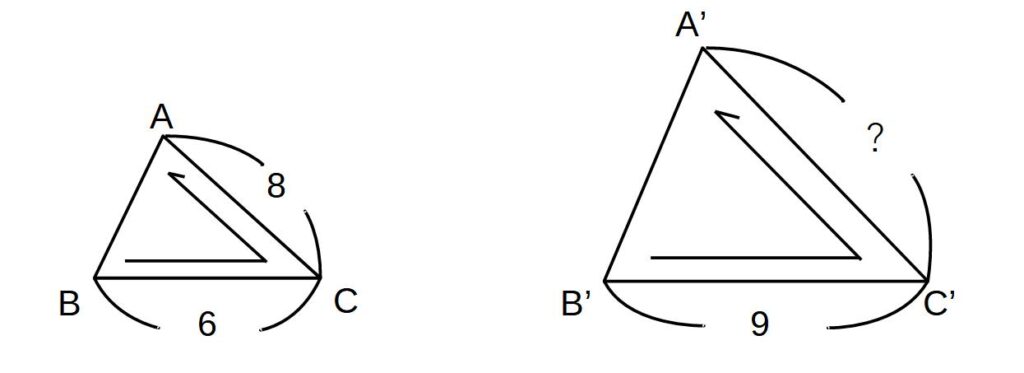
問)相似の△ABCと△A’B’C’がある。
①相似比を答えよ。
②A’C’の長さを答えよ。
①対応する辺 BC:B′C′
= 6 : 9 △ABC:△A′B′C′
= 2 : 3 = 2 : 3
②相似比2:3より
AC:A′C′=2:3
8 :A′C′=2:3
2A′C′=24
A′C′=12
(別解)矢印で比をとる。
BC:AC=B′C′:A′C′
6 : 8 = 9 :A′C′
6A′C′=72
A′C′=12