合同と同様に、相似にも条件があります。
その相似条件のうち、三角形の相似条件を見ていきます。
非常に重要な単元です。入試問題レベルの問題を同時に見ていこうと思います。
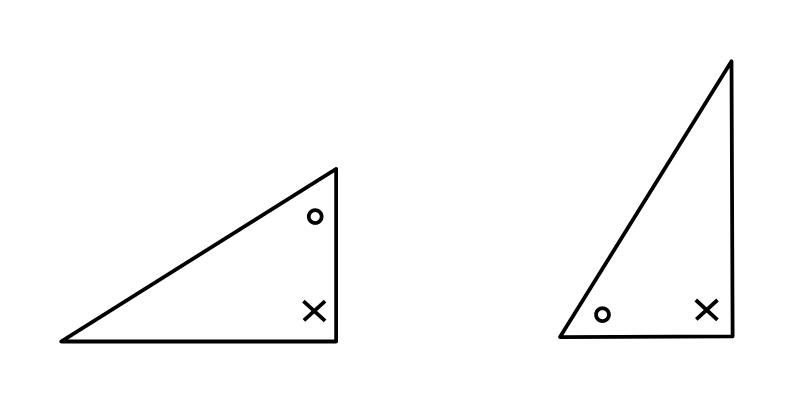
①2組の角がそれぞれ等しい
※向きなどは関係なく、角の等しいところが2つあればよい
→この条件はほとんどの問題で使うといってもいい位よく出る!

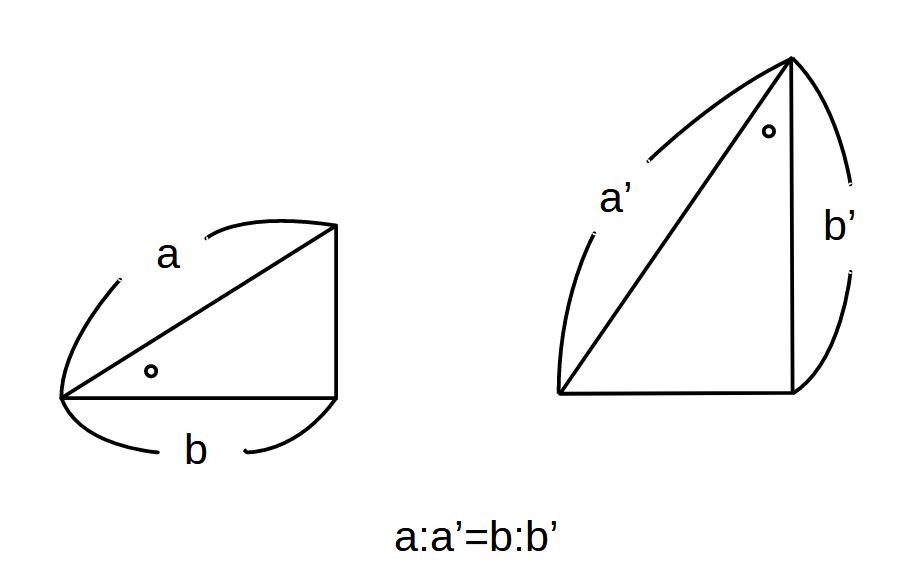
②3組の辺の比がそれぞれ等しい
図の場合は、aとa’、bとb’、cとc’の比がそれぞれ等しい
③2組の辺の比が等しく、その挟む角が等しい
図の場合、aとa’、bとb’の辺の比が等しく、その間の角が等しい
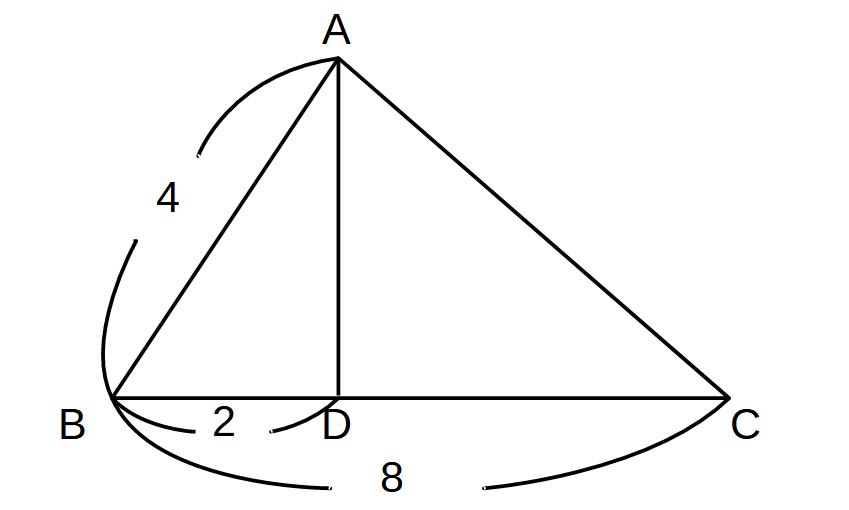
③の条件を見つける問題
※私立高校入試問題出題
△ABD∽△CBA
※合同とは違い、「辺の比」が等しいのであって、「辺」自体がそのまま等しいのではない。
なので、大きさが違っても、相似というものは成り立つ
証明の方法…合同の時と同じ
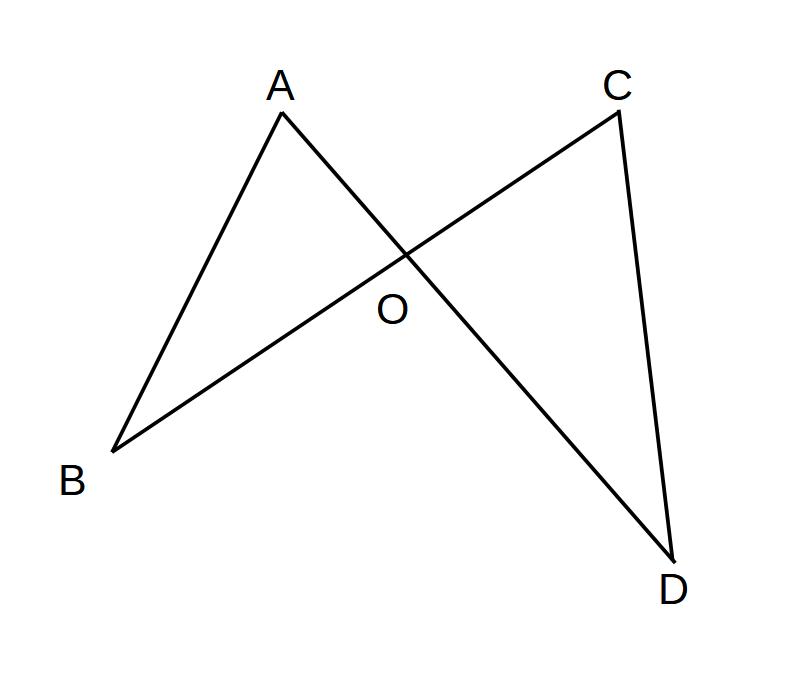
∠BAO=∠DCOのとき、△AOB∽△CODを証明せよ。
(証明)
△AOBと△CODにおいて、
仮定より∠BAO=∠DCO…①
対頂角より∠AOB=∠COD…②
①②より、2組の角がそれぞれ等しいので相似条件
△AOB∽△COD
(例1①)
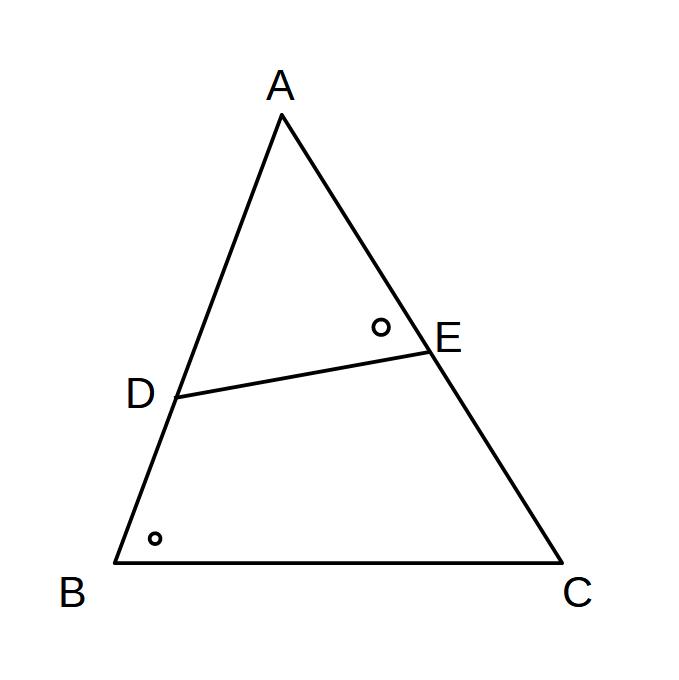
∠AED=∠ABCのとき、△ABC∽△AEDを証明せよ。
(証明)
△ABCと△AEDにおいて
仮定より、∠ABC=∠AED…①
共通な角より、∠CAB=∠DAE…②
①、②より2組の角がそれぞれ等しいので
△ABC∽△AED
(例1②)
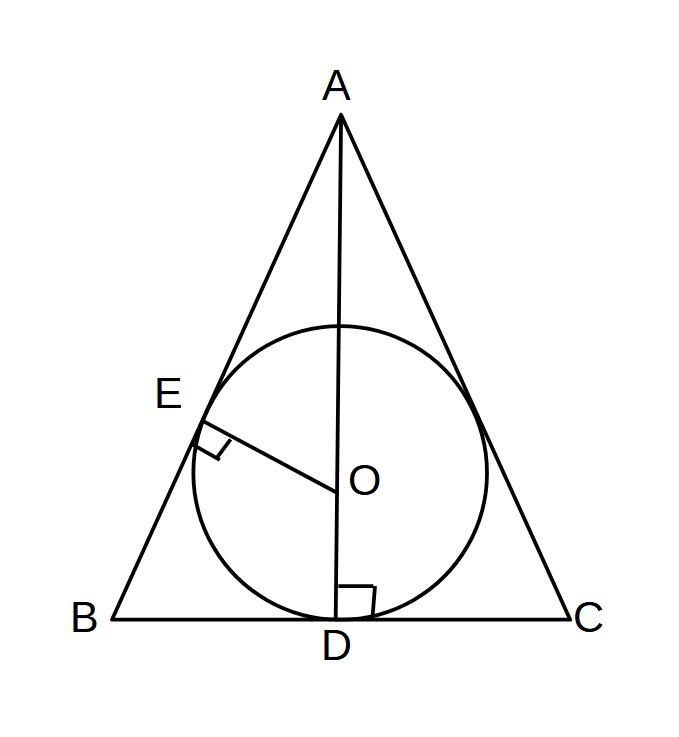
二等辺三角形ABCにおいて、線分ADは∠BACをの二等分線であり、内接円Oの中心Oから線分AB上へ向かって垂線をおろし、線分ABと接した点をEとする。
このとき、△AOE∽△ABDであることを証明せよ。
(証明)△AOE∽△ABDにおいて
仮定より、∠AOE=∠ADB…①
共通な角より、∠OAE=∠BAD…②
①、②より、2組の角がそれぞれ等しいので
△AOE∽△ABD
(例2)
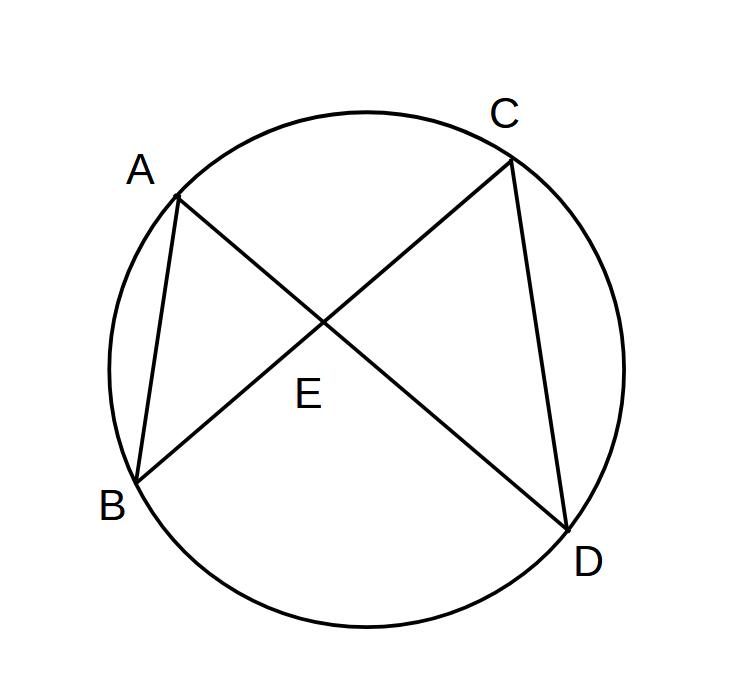
点ABCDはそれぞれ円に内接している。
△AEB∽△CEDを証明せよ
(証明)
△AEBと△CEDにおいて
対頂角より、∠AEB=∠CED…①
同じ弧に対する円周角より、
∠BAE=∠DCE…②
①、②より2組の角がそれぞれ等しいので
△AEB∽△CED
(例3)
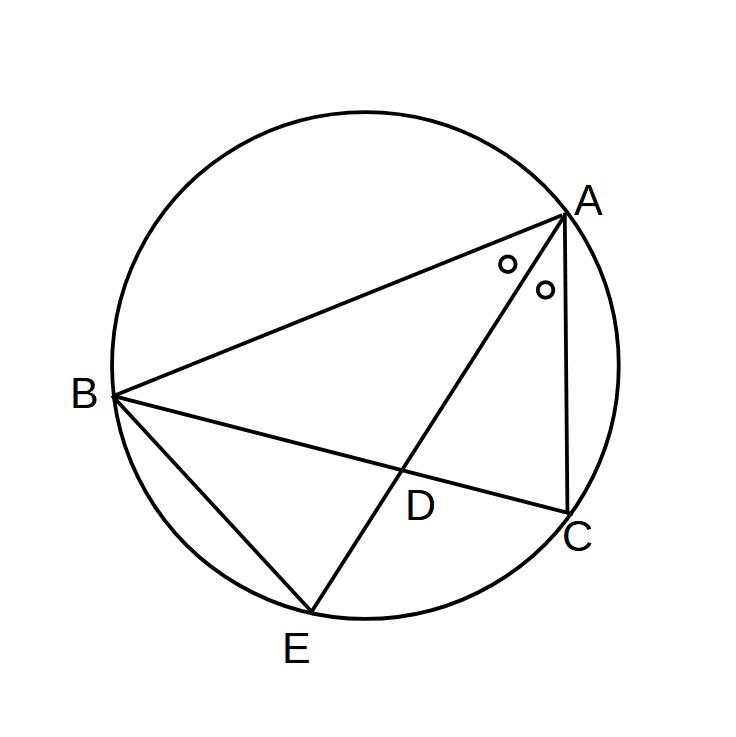
線分AEが∠BACの2等分線のとき、△ABE∽△ADCを証明せよ。
(証明)
仮定より∠BAE=∠DAC…①
同じ弧に対する円周角より
∠AEB=∠ACD…②
①、②より、2組の角がそれぞれ等しいので
△ABE∽△ADC