中点連結定理については、中2でやっていますが、それを比で表せるようになりましょう。
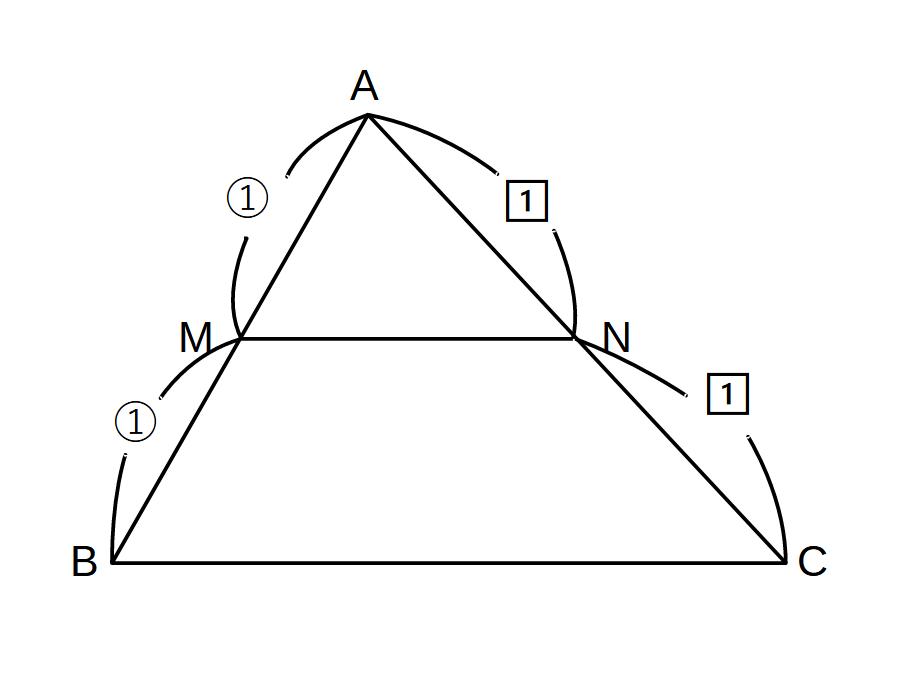
M、Nが中点ならば、
△AMN∽△ABC(MN//BC)
= 1 : 2
※逆も成り立つ
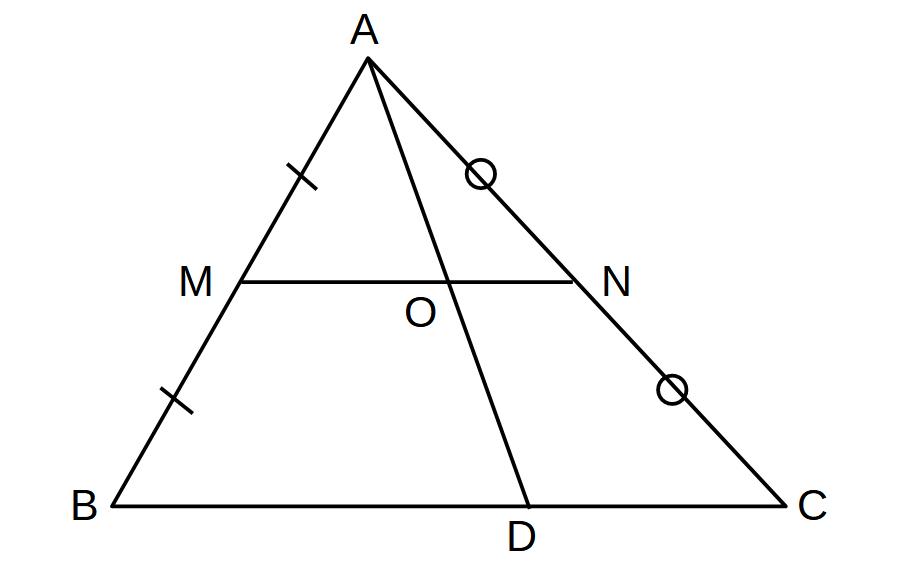
△ABDで中点連結定理が使える!
AO:OD=1:1
(OはADの中点)

①AB、PR、PQを求めよ。
AB:QR=2:1 AB:14=2:1 ∴AB=28
PR:AC=1:2 PR:30=1:2 ∴PR=15
PQ:BC=1:2 PQ:26=1:2 ∴PQ=13
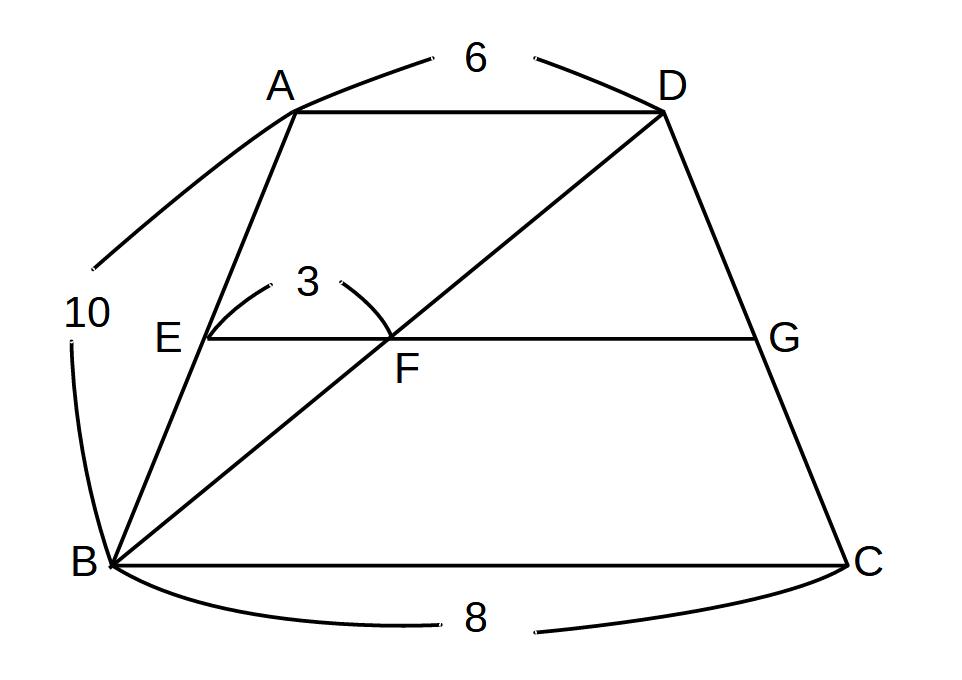
②AD//EG//BCのとき
(1)AEの長さ
(2)FGの長さ
を求めよ。
AD//EF、AD:EF=2:1より
△BEF∽△BAD
(1)EはABの中点より
AE=5
(2)AE:EB=DG:GC=1:1
FG:BC=1:2
FG:8=1:2
FG=4
②の裏技として、図の公式を使って
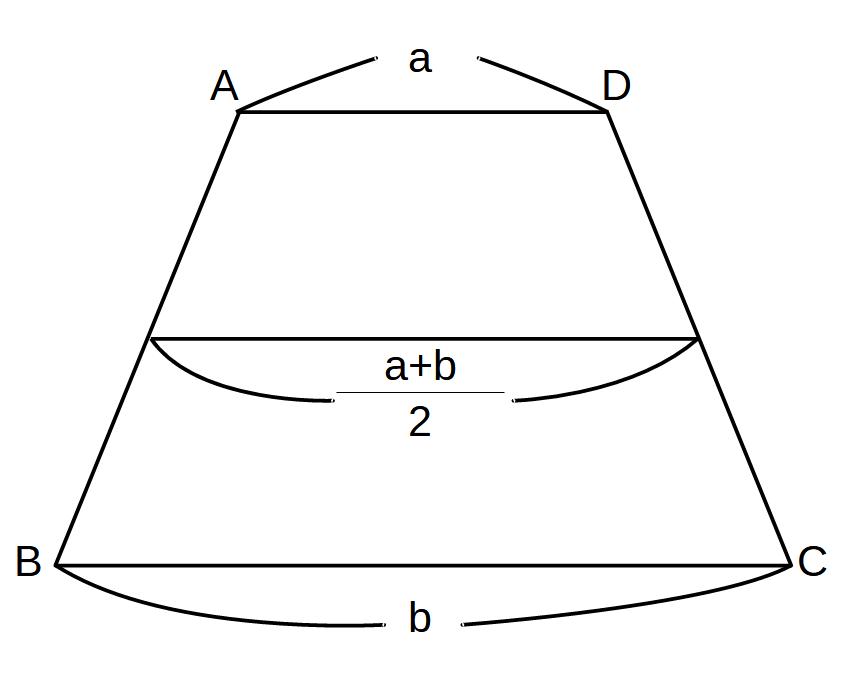
\( \displaystyle EG= \frac{(6+8)}{2} =7 \)
\( FG=7-3=4\)
とすることもできる!