(1)三平方の定理

例
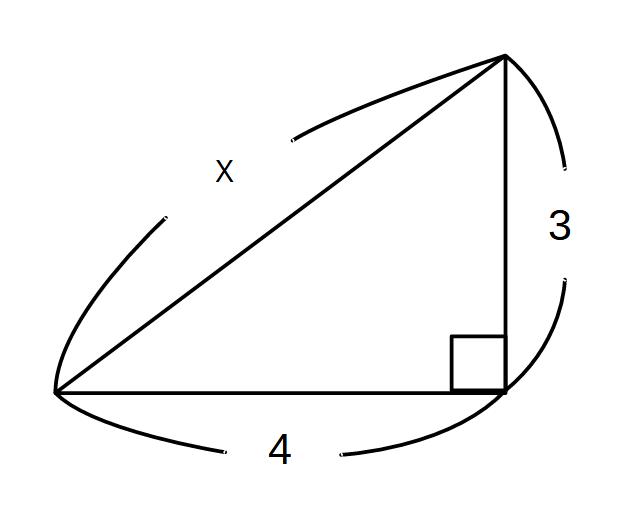
①
x2=32+42
x2=9+16
x2=25 x>0
x=5
(-5はなし。長さにマイナスはないです)
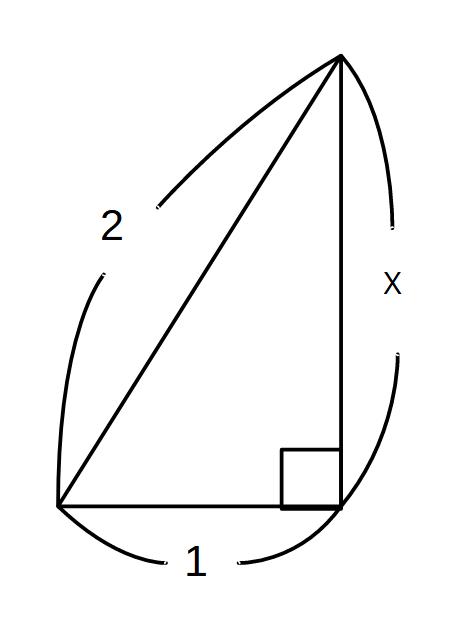
②
22=x2+12
4=x2+1
x2=3 x>0
x=\( \sqrt{3}\)
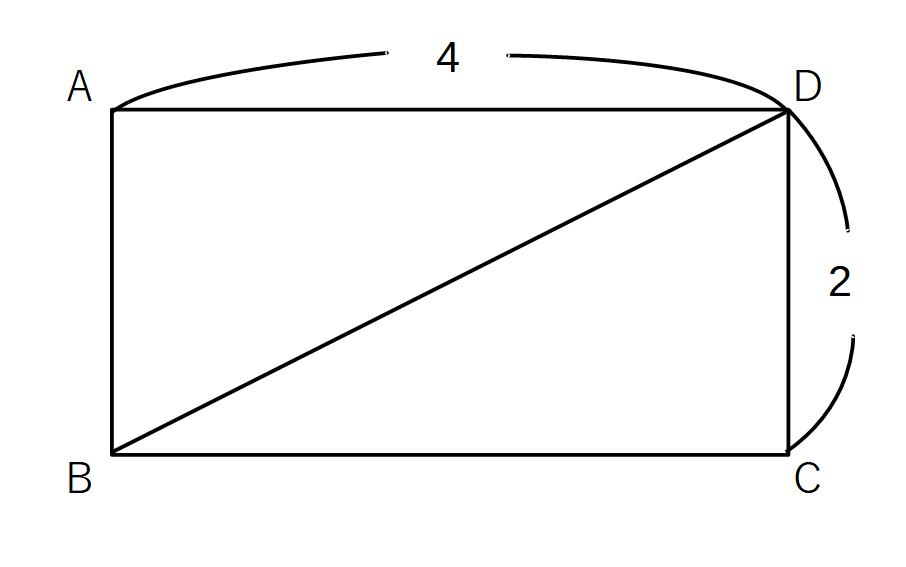
①対角線の長さを求める
BD2=DC2+BC2
BD2=42+22
BD2=16+4
BD2=20 x>0
BD=\( \sqrt{20}=2\sqrt{5}\)
②高さを求める
AB2=BD2+AD2
32=22+AD2
9 =4+AD2
AD2=5 x>0
AD=\( \sqrt{5}\)
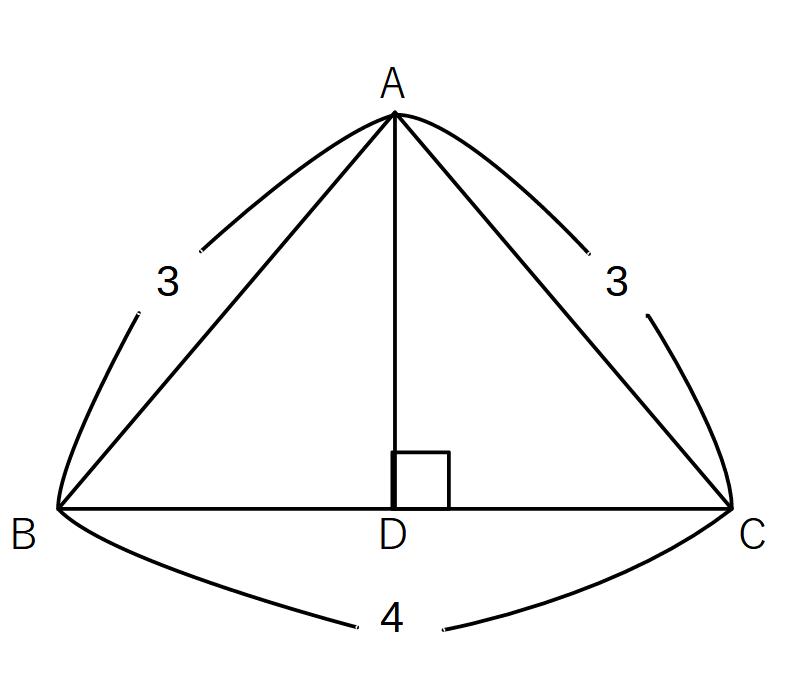
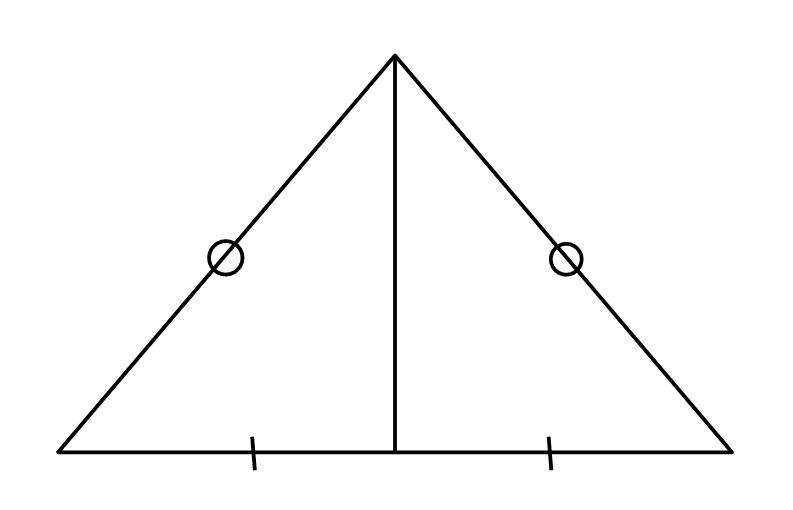
※②のBDが2であることについて、二等辺三角形の性質を再度おさらいしておきます。
頂角から下ろした垂線は底辺を二等分する(底辺の中点を通る)ので、BDはBCの半分の2である。
(2)三平方の定理の証明
定期テストで出題される可能性があるのが定理の証明です。
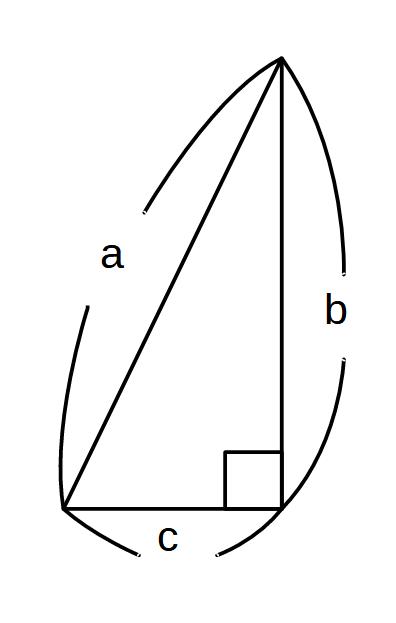
(証明)
4枚の合同な直角三角形を使います。
まず、xを90°であることを証明します。
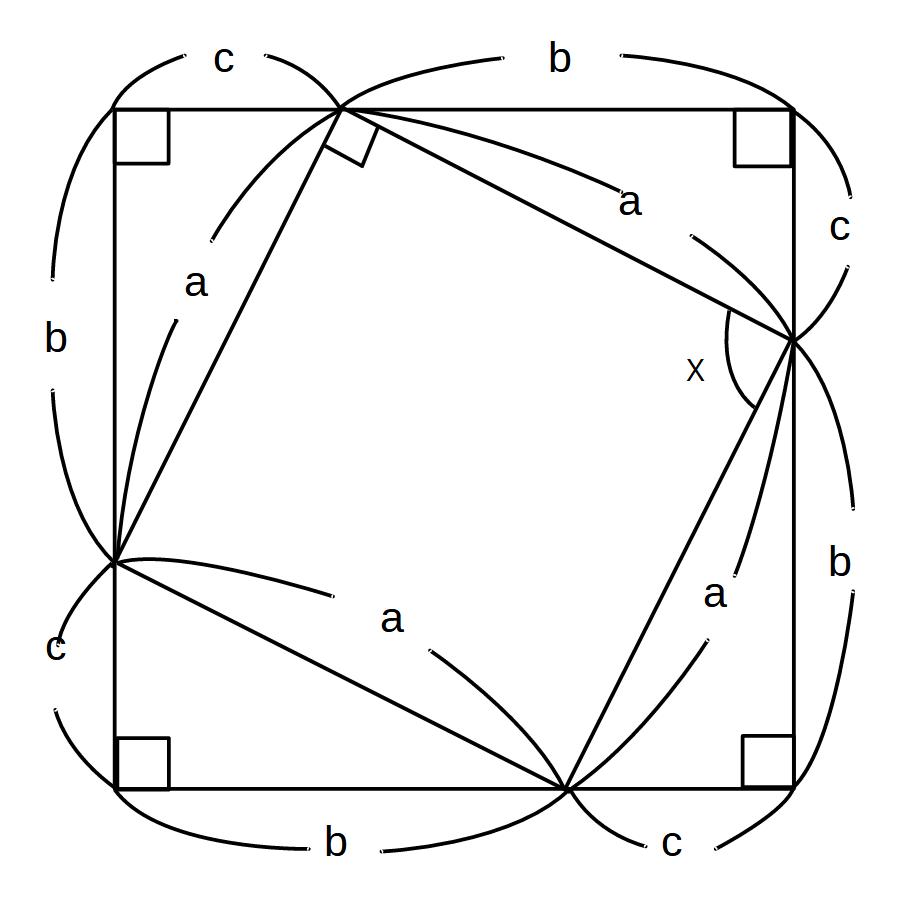
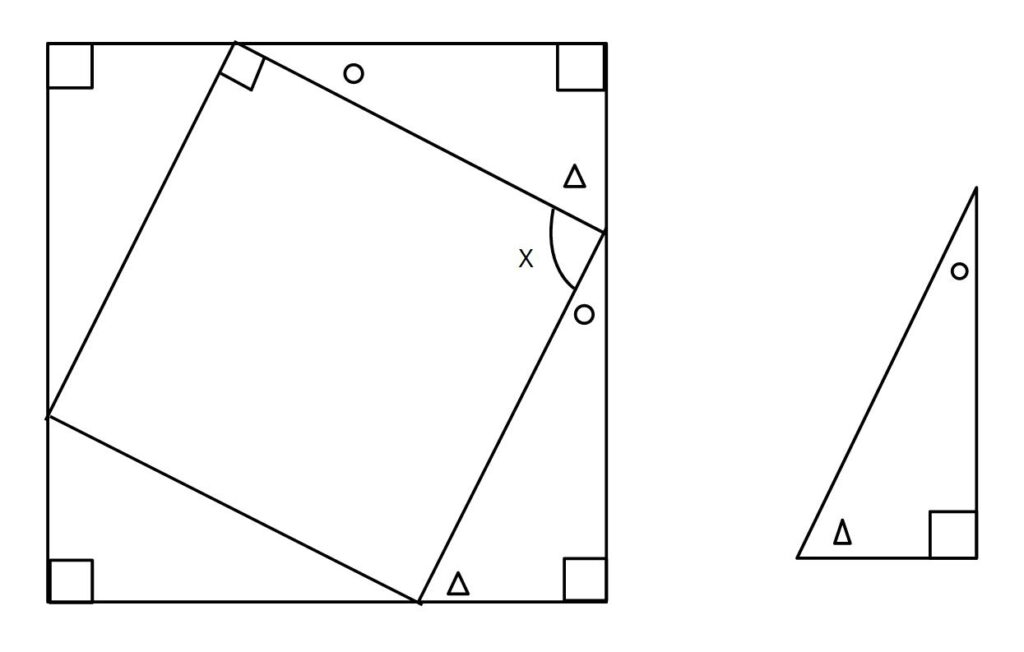
〇+△=90°
x=180ー(〇+△)
x=90°
四角形の面積を2通りで求めます。
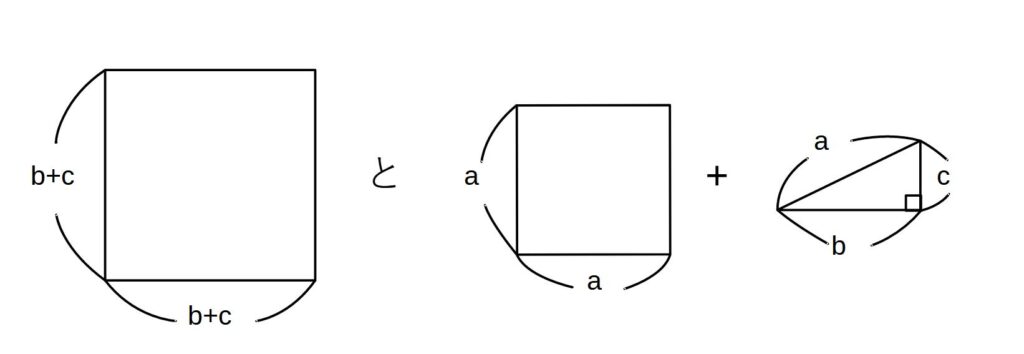
\( \displaystyle (b+c)^2= \frac{1}{2}bc \times 4+a^2\)
\( b^2+2bc+c^2=2bc+a^2\)
\( b^2+c^2=a^2 \)