例1ー1)
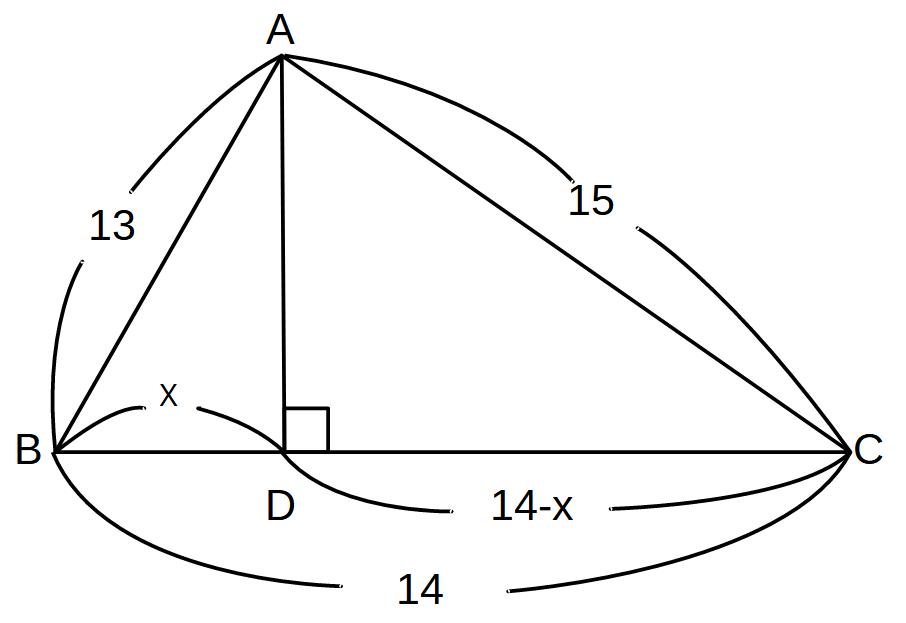
(1)ADの長さ
(2)△ABCの面積
をそれぞれ求めよ。
BD=xとおく。
DC=14-x
(1)△ABDで三平方
AB2=BD2+AD2
169=x2+AD2…①
△ADCで三平方
AC2=DC2+AD2
225=(14-x)2+AD2…②
①、②で連立する
①AD2=169-x2
②AD2=225-(14-x)2
169-x2=225-(14-x)2
169-x2=225-(196-28x+x2)
169-x2=225-196+28x-x2
140=28x
x=5
①に代入して、
AD2=169-25
AD2=144 AD>0
AD=12
(2)△ABC=14×12×1/2=84
例1-2)
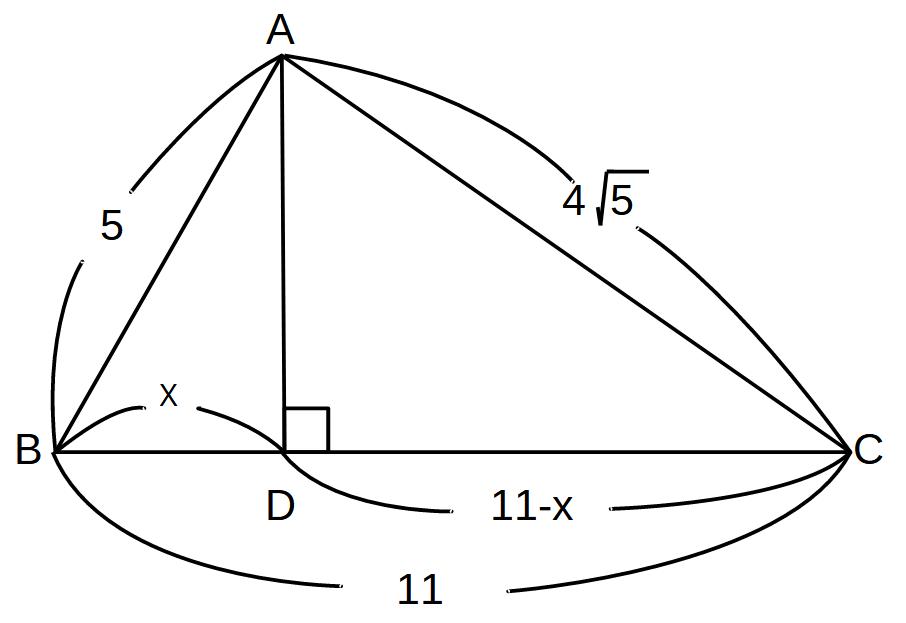
(1)ADの長さ
(2)△ABCの面積
をそれぞれ求めよ。
BD=x
DC=11-x
(1)△ABDで
52=AD2+x2…①
△ACDで
(4√5)2=AD2+(11-x)2…②
①②を連立
①AD2=25-x2
②AD2=80-(11-x)2
AD2=80-(121-22x+x2)
AD2=-x2+22x-41
25-x2=-x2+22x-41
22x=66
x=3
①に代入
52=AD2+32
AD2=25-9
AD2=16 AD>0
AD=4
(2)△ABD=11×4×1/2=22
例2ー1)折り返し
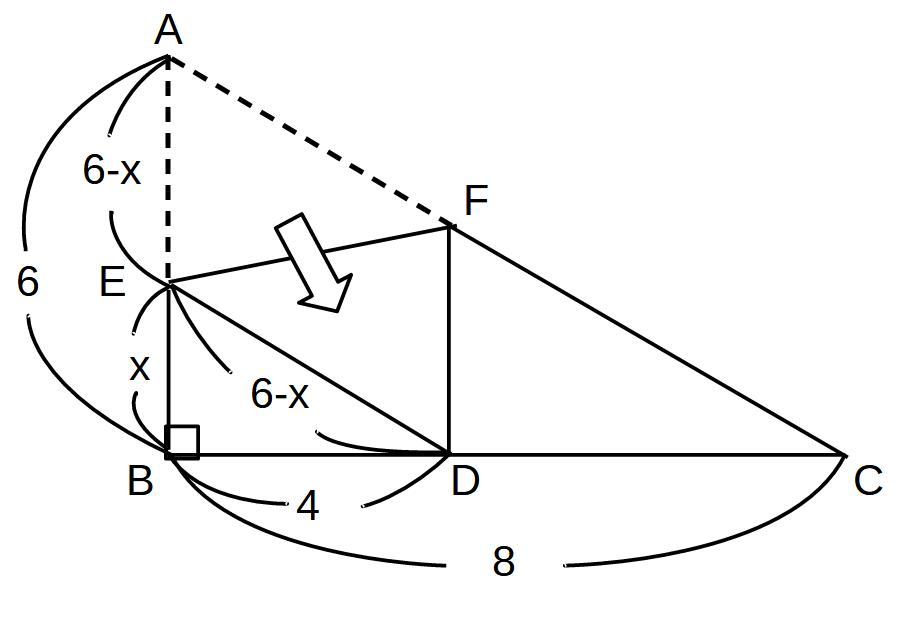
AB=6cm、BC=8cm、DはBCの中点のとき、BEの長さを求めよ。
※直角三角形の3辺のうちわからないところをxでおく!
BE=x
AE=ED=6-x
△BEDだけ切り抜きます。
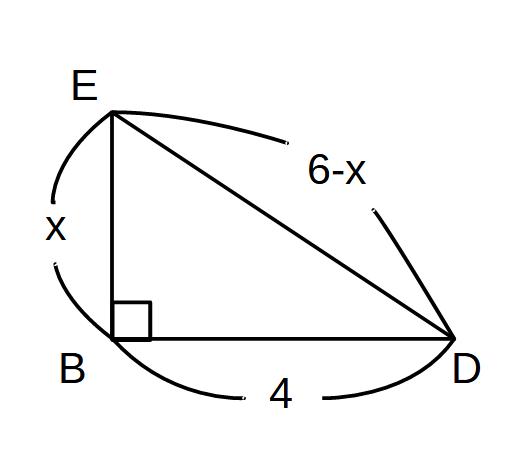
(方程式)
(6-x)2=x2+42
-12x=-20
x=5/3
BE=5/3cm
例2-2)
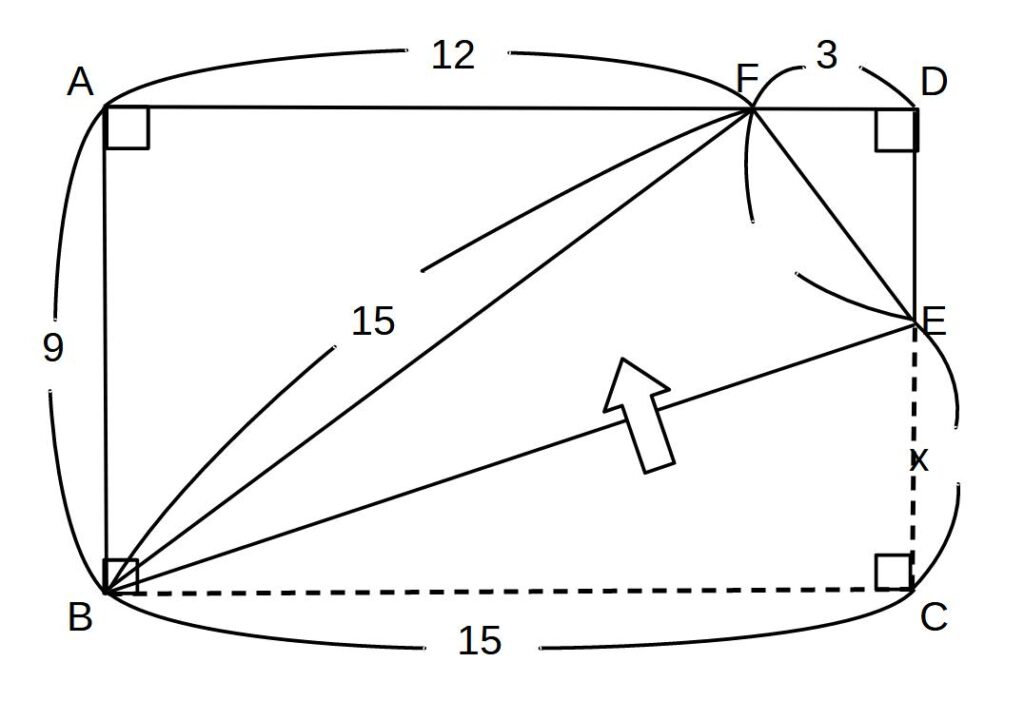
AB=9cm、BC=15cmの長方形がある。
CとFが重なるように折り返した。
①CEの長さ
②BEの長さ
をそれぞれ求めよ。
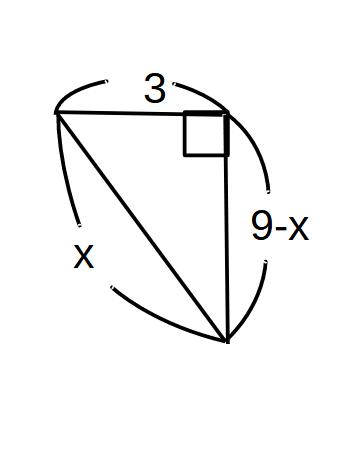
(1)CE
CE=EF=x
AE2=152-92 AE>0
AE=12 x2=32+(9-x)
FD=3 x2=9+81-18x+x
DE=9-x 18x=90
x=5
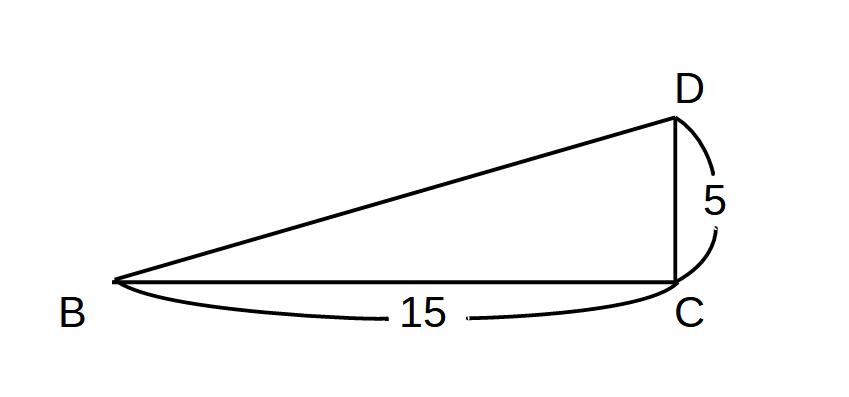
BE2=52+152
BE2=250 BE>0
BE=5√10