(1)正四角すい
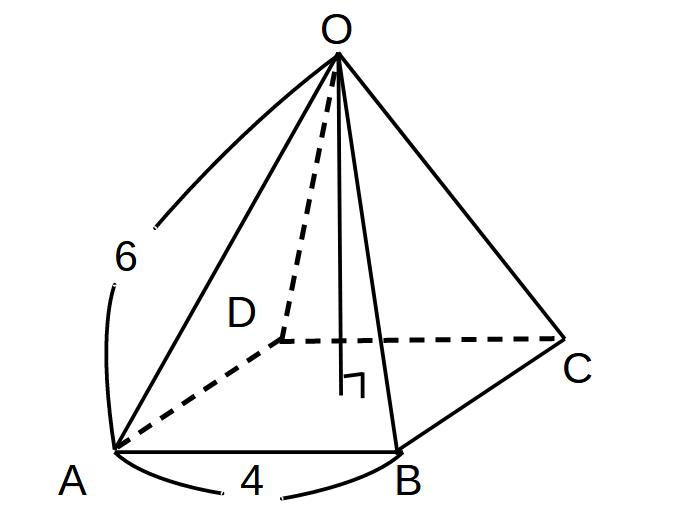
底面の正方形の1辺が4cm、他の辺が6cmである正四角すいの高さを求めよ。
※正四角すいの場合、高さをとるとすると、底面の対角線の交点からOまでの距離が高さになる!
わかりやすく分離して図示します。
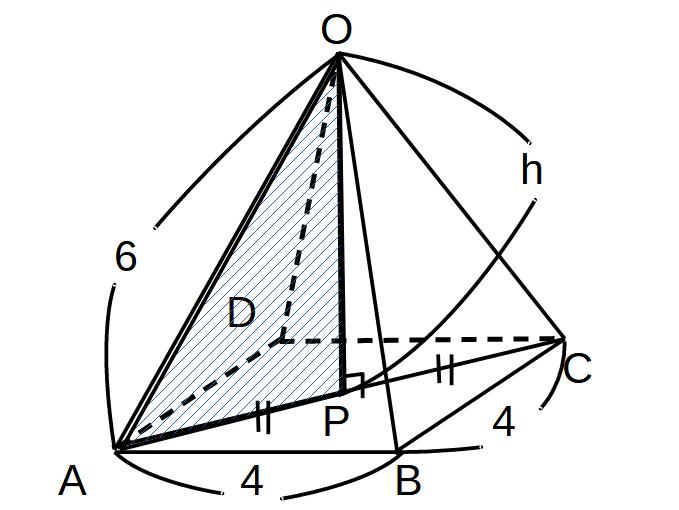
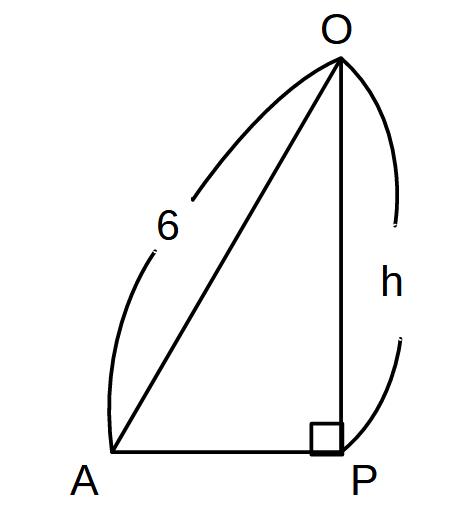
APの長さがわからないとh(高さ)が求まらないので、次は、対角線の交点Pを含む三角形ABCを見ていきます。
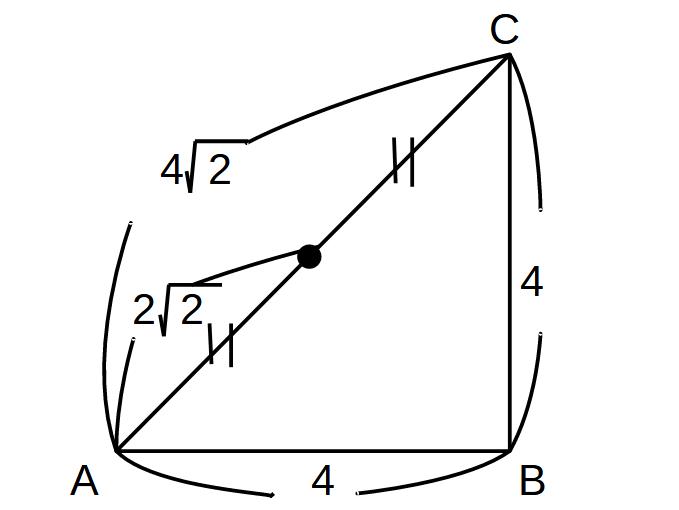
正四角すいなので、底面ABCDは正方形です。
それを対角線で半分にしているので、直角二等辺三角形になります。
ということは、辺の比は1:1:√2になります。辺ACの長さは4√2となり、APの長さは、
\( \displaystyle AP=4\sqrt{2} \times \frac{1}{2} =2\sqrt{2} \)
となります。
では、△OAPに戻って計算です。
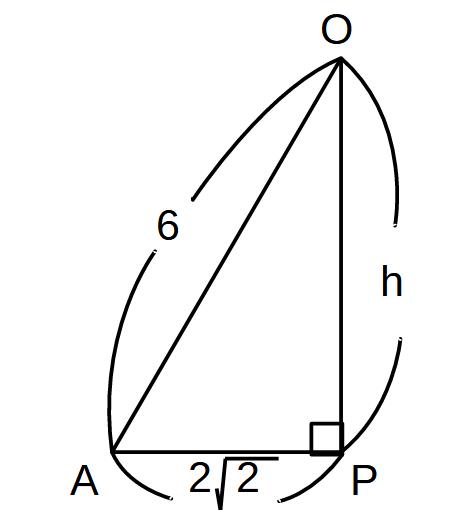
APの長さがわかっているので、
h2=36-8
h2=√28
h=±2√ 7
h=2√ 7
※発展…切頭図形
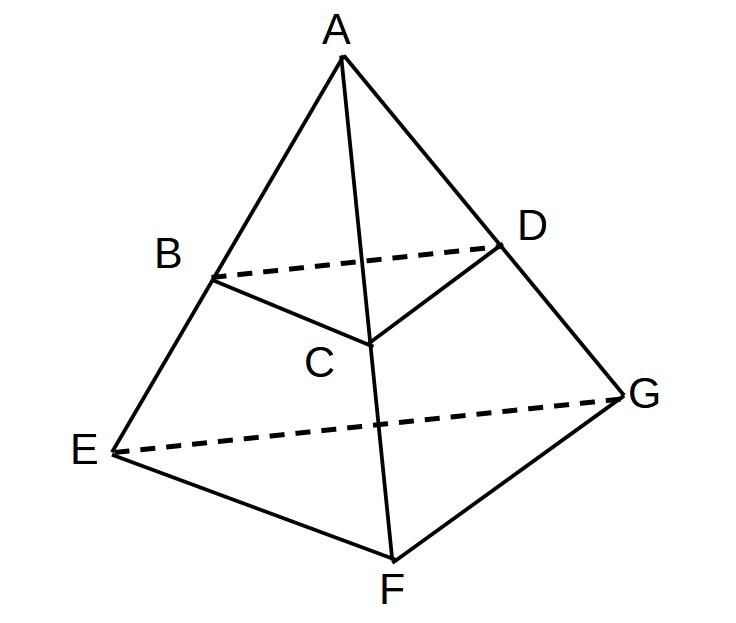
図の三角錐における、
A-BCD:A-EFG
の体積比はどうなるでしょうか。
A-BCD:A-EFG=1:15
つまり、上の土台は1に対し、下の土台は14という比率になります。
(2)三角柱
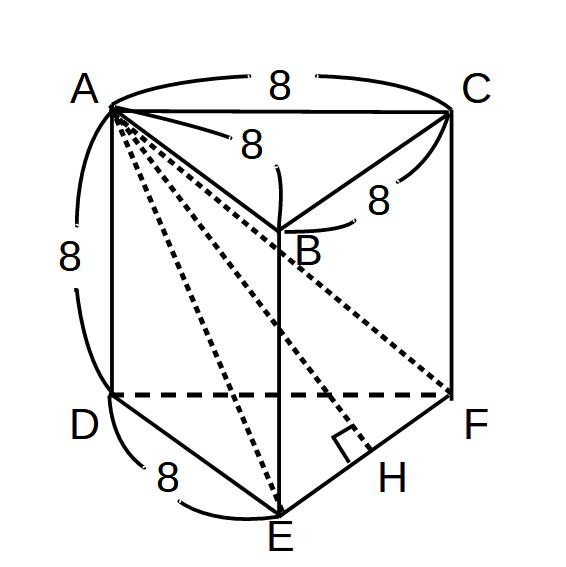
図のように1辺が8の三角柱がある。
頂点Aから辺EFにひいた垂線AHを求めよ。
※AH⇒△AEFで考える!
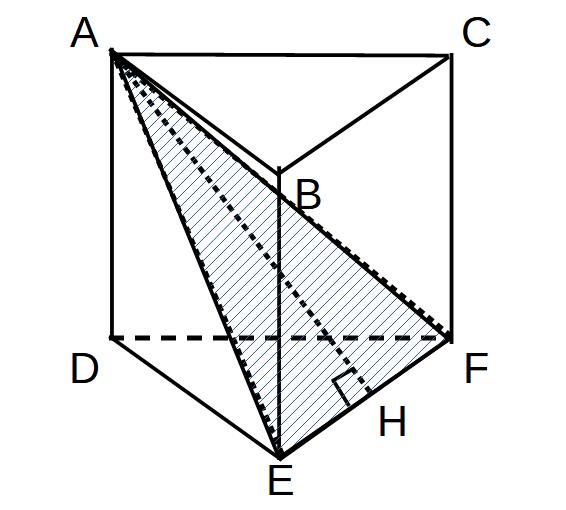
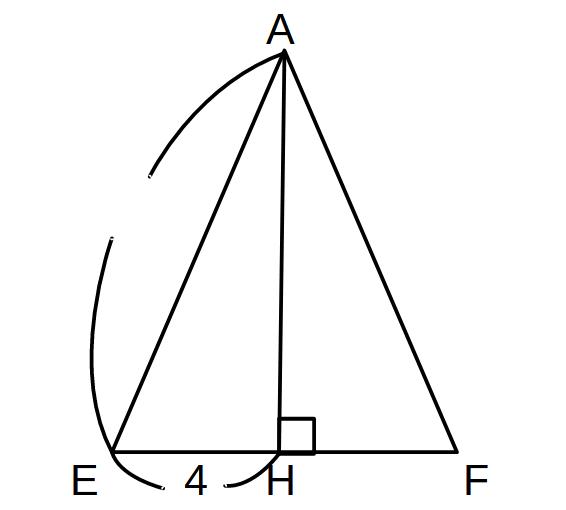
AEの長さがわからないので、AHの長さが出せません。なので、AEを求めるために、四角形ABEDを切り取って計算します。
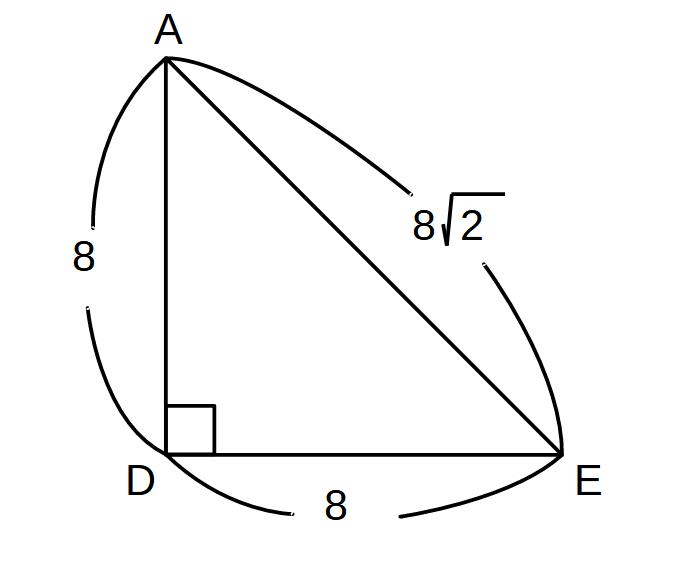
すべて1辺が8なので、四角形ABEDは正方形です。それを対角線で半分なので、直角二等辺三角形になります。
そうなると辺の比が1:1:√2になり、AEの長さが8√2となります。
△AEHに戻ります。
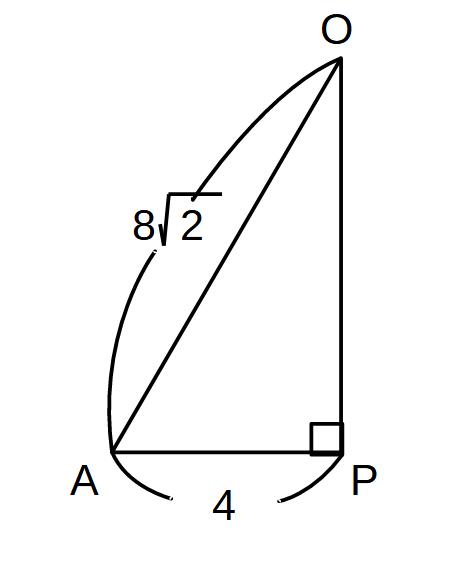
辺AO、辺APがわかったので、あとは計算です。
AH2=128-16=112
AH=±4√ 7
AH=4√ 7