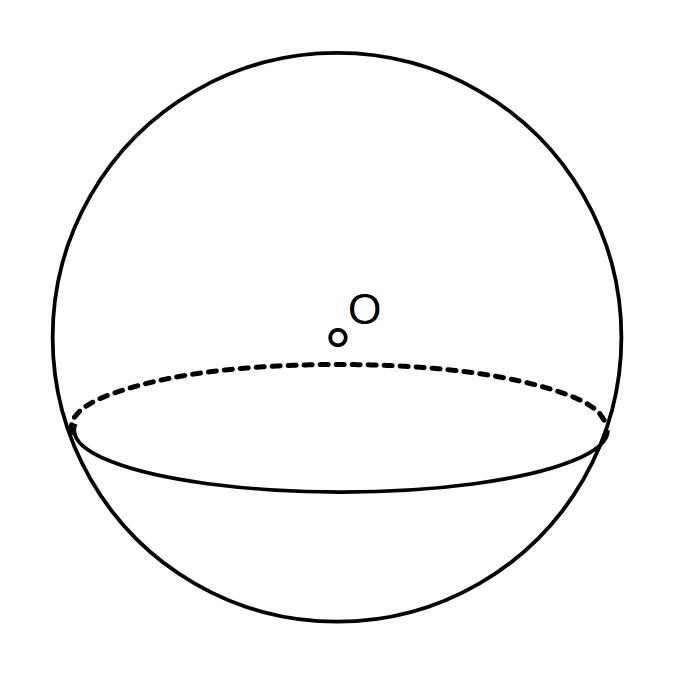
半径15cmの球を、中心からの距離が12cmの平面で切るとき、切り口の円の半径と面積を求めよ。
※球の切り口は、円になるので、面積は円の面積になる
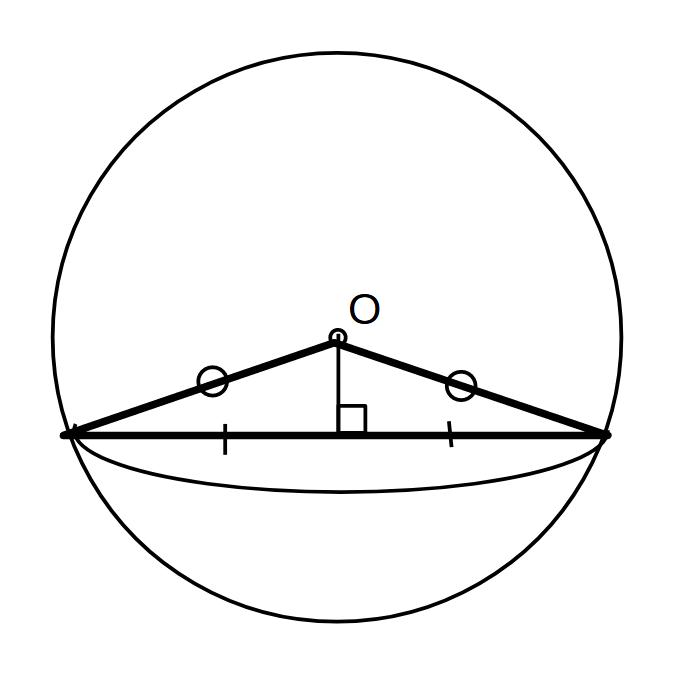
球の切り口は、円になるので、中心からある一定の離れた距離の平面で切った場合、その縁から中心へはすべて等しい距離になり、円すいを形成し、それを中心Oをとおる線で切断すると、中心Oを頂角とした二等辺三角形を形成します。
なので、その二等辺三角形を切り取ってみていきます。
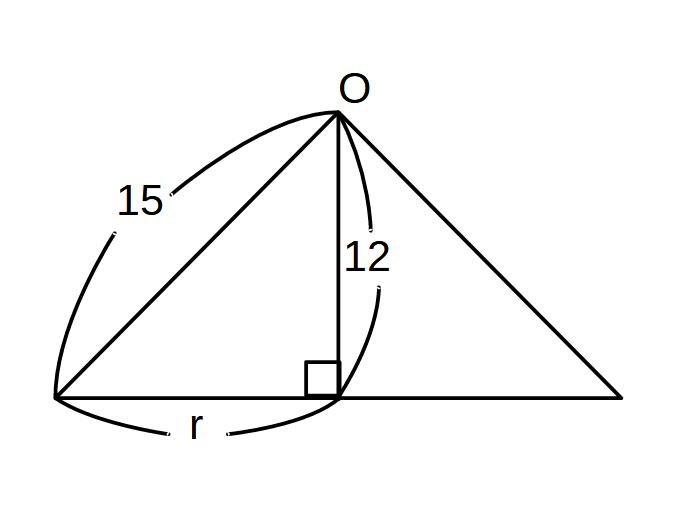
これで、三平方の定理を使って半径を計算します。
r2=152-122=225-144=81
r=±9
r=9 ∴半径9
面積=9×9×π=81π
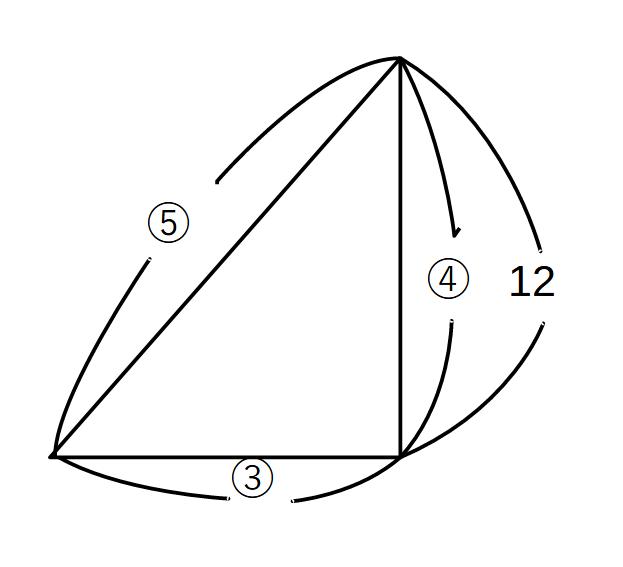
※ちなみに、二等辺三角形になってから、この方法で計算できます。
気づいた方もいらっしゃるかもですが、この二等辺三角形が3:4:5の比になっています。
比を使って計算も可能です。
12:r=4:3
4r=36
r=9