(1)直方体
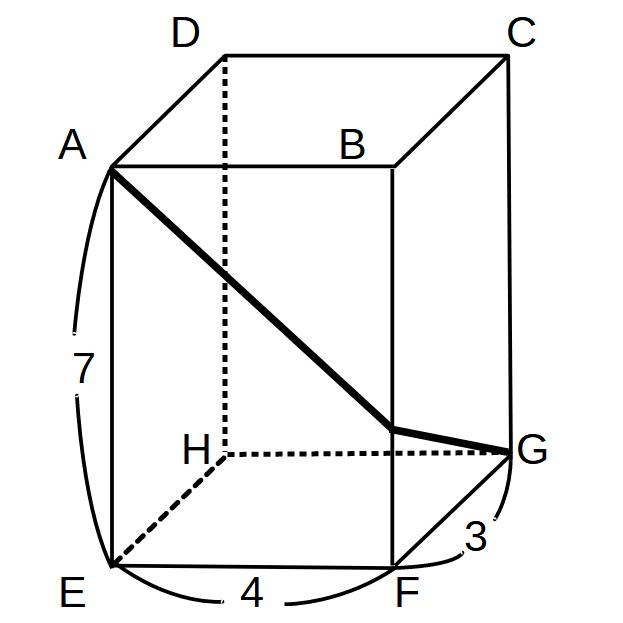
図のように、A-Hまでの頂点を持つ直方体がある。
頂点AからGまで糸をかけるとき、糸の最小の長さを求めよ。
※糸が通る面で考えます。
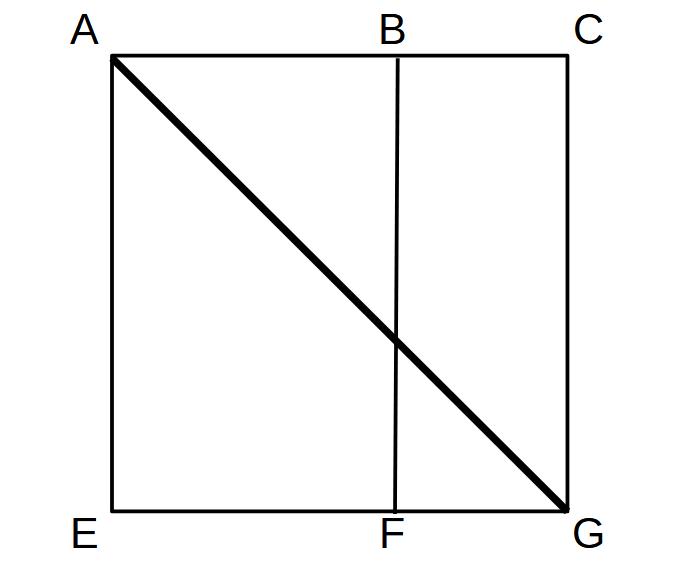
糸が通る面だけを切り取って1つの面にしてみました。
面AEFB→面BFGC
糸が通る最短距離→一直線!
AG2=72+72=98
AG=±7√ 2
AG=7√ 2
(2)円すい
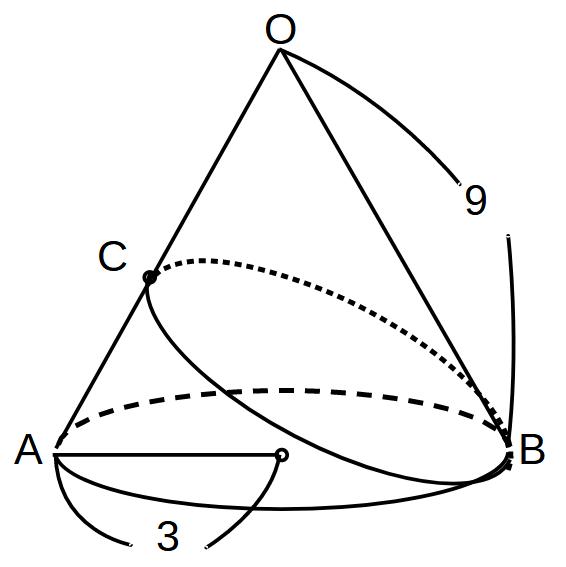
図のような円すいがある。
Bから側面を1周させて糸をまくとき、糸の最小の長さを求めよ。
※展開させて平面で考える
→側面のおうぎ形で考えます。
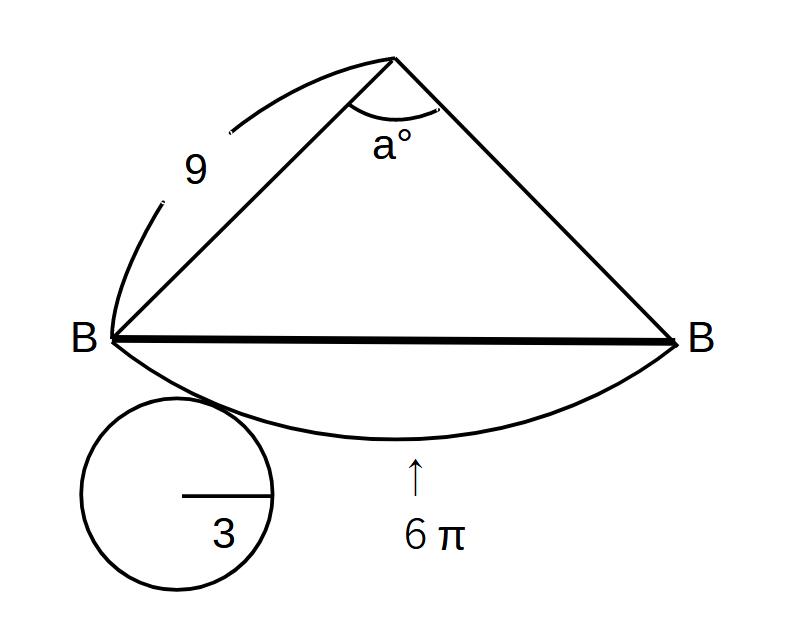
中心角=弧/円周×360°
a°=6π/18π×360°
=120°

B~Bまでが最短距離になります。
1:2:√3があてはまるので、長さがわかります。
9/2√3×2=9√3
最短距離=一直線になる、ということを覚えておきましょう。