前回は、中学校では文字を使った式を使用することを勉強しました。
今回は、その書き方のルールを勉強します。
(1)文字のかけ算
全部で6つにまとめました。覚えましょう。
ルール① 記号(×「かける」)は省く
例)3×x → 3x a×b → ab
ルール② 数字は文字の前に (数字→文字)
例)x×80 → 80x
ルール③ 1×x や (ー1)×a など、数字が 1,ー1の時は「1」を省く
例)1×x = 1x = x
(ー1)×a = ー1a = ーa
ルール④ 文字×文字はアルファベット順に並べる
例)z×x×y = xyz
b×a = ab
ルール⑤ 同じ文字のかけ算は累乗にする
例)z×z×z = z3
b×b = b2
ルール⑥ (文字の式)×数字 は、数を()の前に置き、×(かける)は省く
例)(a+b)×3 = 3(a+b)
(y+3)×(-2) = -2(y+3)
(2)文字のわり算

※上の分数の表し方について
文字を分子において表記する方法と、分子は数字のみにして、文字は右に出して表記する方法の2通りがあります。どちらも使用することがありますので、両方とも書くことができるようにしましょう。
分子に文字を置く方法 → 加減法でつかう
分子に文字を置かない方法 → 乗除法でつかう
(3)加減乗除の混ざった計算
ルール①
乗除算については、(1)(2)のルールにのっとる
例)
①$$(a)\times(3)\div(b)=\frac{3a}{b}$$
②$$(x)\div(7)\div(y)=x\times\frac{1}{7}\times\frac{1}{y}=\frac{x}{7y}$$
ルール②
加減算は残しておいて、ルール①で作った乗除のひとかたまりを使って加減の式を作る
例)
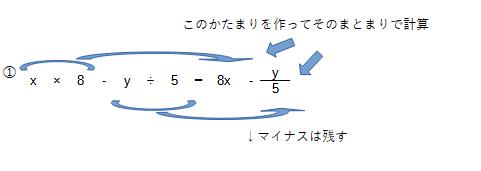
順番として、①乗除(かけ算・わり算)→②加減(足し算・引き算)の順は、基本的に変わらないので、文字が入って見慣れない形が出てきてもルールさえしっかり守って計算をすればよいです。もちろん、かっこがあればその順番を守るように。
注意)a÷(-7)2
\( \displaystyle a\div(-7)^2=\frac{a}{49}\) ←かっこから計算するとこうなる。が…
\(a\div(-7)\times(-7)\)としてしまうと…
\(=a\) =???
このようなミスが散見されます。かっこの計算は先にするなど、正負の数でやった計算のルールがここでも適用されるので、しっかりと復習をしましょう。
今回は文字式の計算ルールを勉強しました。
正負の数からのルールがすべて必要になってきますので、計算問題をたくさん解いて復習をしておくようにしましょう。