今回は、文字を使って、数量を表す方法を勉強します。
(1)代金・個数
①代金→(商品1つの値段)×(個数)
例)1個80円のねぎを6本買った
80×6=480(円) ←小学校の時習ったやつです
1個80円のねぎをa本買った
80×a=80a(円)
1個x円のねぎを12本買った
x×12=12x(円)
→問題文で文字を使用されている場合、文字と数字をつなげた式を作りましょう。小学校の時みたいに完全に数字での答えが出ないのが最初は慣れないと思いますが、これからはこういった使い方はたくさん出てきます。慣れていきましょう。
②残りの量 → (元の量)ー(使った量)
例)15個のりんごを4人に3つずつわけた余り
15-4×3=15-12=3(個)
15個のぶどうをx人に4つずつわけた余り
15-x×4=15-4x(個)
y個の栗をx人に5個ずつわけた余り
yーx×5=yー5x(個)
1個100円のノートをx冊買って、1000円出した時のおつり
ノートの代金 → 100x(円)
おつり=出したお金ー代金
1000-100x(円)
(2)整数
文字を使った数の表し方 ← テストの文章題で使われる!
①連続する3つの数
1番小さい数をnとする → n , n+1 , n+2 と表す
②奇数と偶数
偶数 → 2で割ることができる = 2の倍数ということ
ということは、ある整数に2をかけると偶数になる
ある整数→nとすると、偶数=2n と表す
奇数 → 2で割ると1余る数ということ
ということは、偶数+1 → 2n+1 と表す
③連続する3つの偶数、連続する3つの奇数
奇数 → 1 → 3 → 5 → 7
※奇数偶数ともに2ずつ増えていく!
偶数 → 2 → 4 → 6 → 8
つまり、文字で表すと、
連続する3つの奇数 2n+1 , 2n+3 , 2n+5 , …
連続する3つの偶数 2n , 2n+2 , 2n+4 , …
と表す
④2けたの整数、3けたの整数
2けたの場合
67 = 60+7 = 6×10+3
24 = 20+4 = 2×10+4 のように表せる
では、10の位をa、1の位をbと置くと 10a+b と表す
3けたの場合
352 = 300+50+2 = 3×100+5×10+2
100の位→a、10の位→b、1の位→cと置くと 100a+10b+c となる
⑤わられる数
(わられる数) = (わる数) × (商) + (余り)
例)6でわると商がxで余りが4になる数 6x+4
2でわると商がaで余りがbになる数 2a+b
→この整数の表現は、説明されていても「なんのこっちゃ」と思うかもしれませんが、上でも書いたようにテストの文章題で出てくる重要な部分でもあります。まずは問題を解いて「こういうものなのか」くらいでもいいので覚えておきましょう。
(3)平均

ちょっとひねった平均の問題 ← テストでは主にこんな感じで出そう

(4)速さ
速さの計算
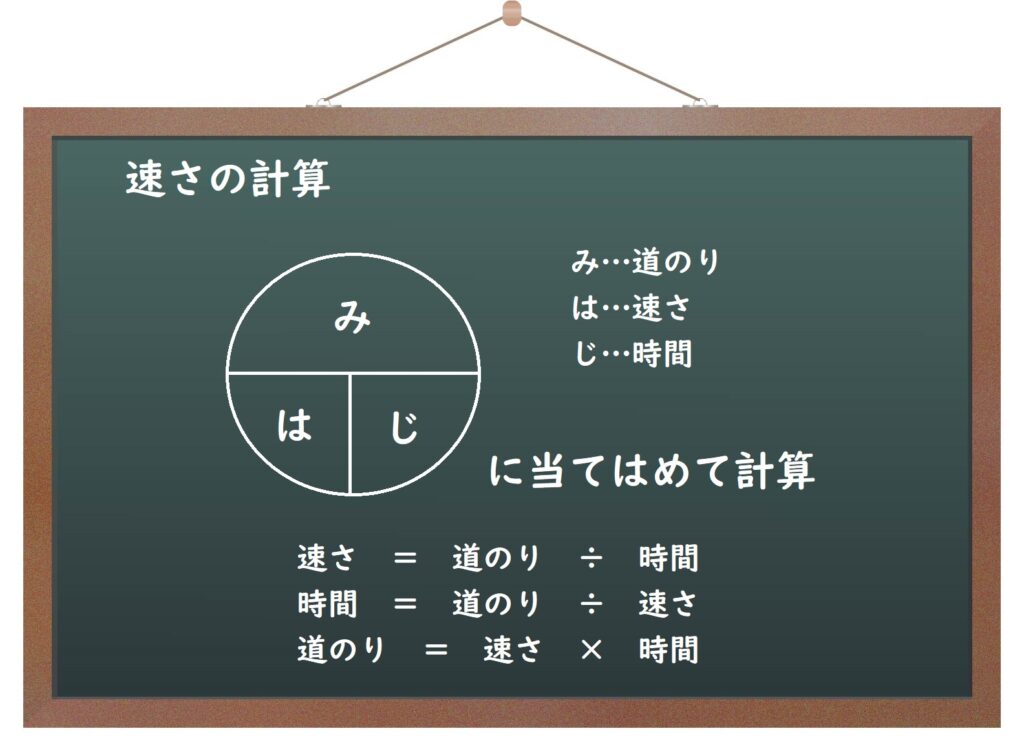
なぜこんな円の中に収めているかというと、円の中の横線は分数の意味と考えて、縦線はかけ算と考えてもらえれば、この円を覚えておくだけで何と何を計算すれば何が求められるかわかるからです。
あと、気を付けてもらいたいのは、単位をそろえてから計算をするようにしてください。(時速、分速やm、km、時、分など)
なお、ここからは新しく覚えてもらうことですが、もちろん、式の中に文字が入ってきたら以下のように文字を式に入れて表してください。
例)xkmの道のりを3時間かかって歩いた時の速さ

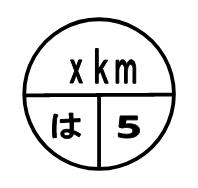
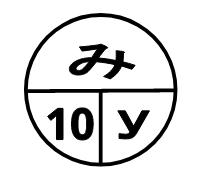
例)xkmの道のりを毎時10kmでy時間走った時の残りの距離
走った距離 = 10y(km)
残り = x-10y(km)
(5)割合の表し方

小学校でも割合の計算はありましたが、主に小数で表していたため、分数で計算するのは慣れていないかもしれません。しかし、これからは分数で計算することが多くなるので、少しずつでも分数での計算に慣れていくとよいでしょう。ただし、慣れないうちから無理にせず、あくまで慣れてからゆっくりでいいので、分数になじんでいってください。
あと、割合ではテスト等問題でこのような表現をしてくる場合があります。
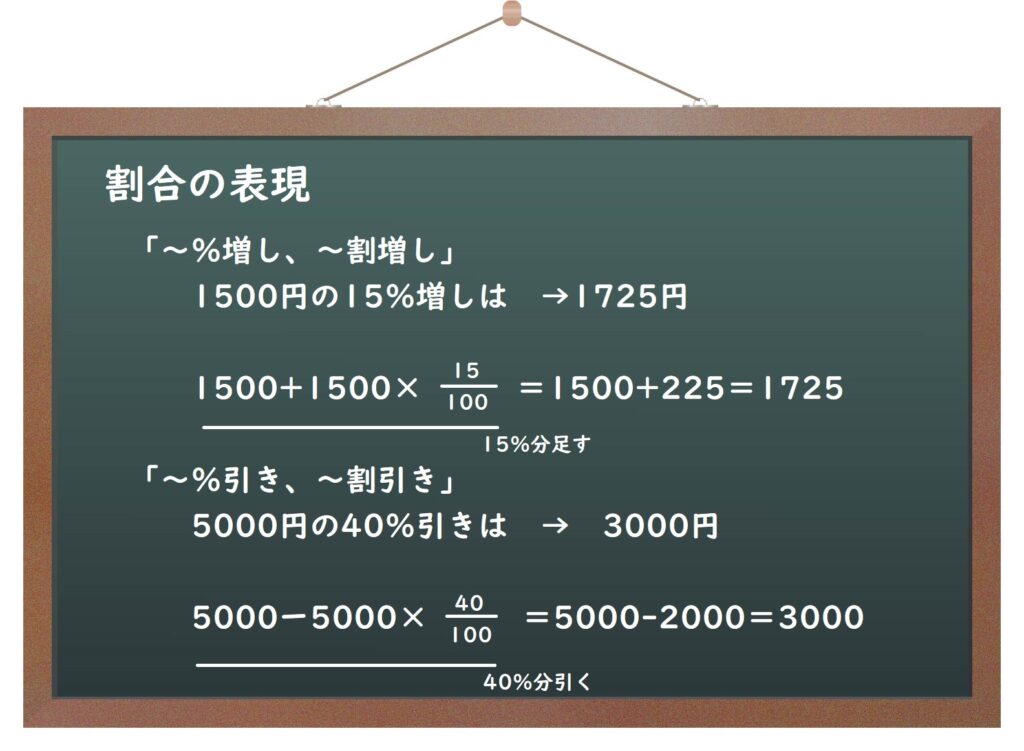
ということは、当然ですが、今までの式の中に文字が入っていたら、その文字を入れて式を作ることになります。ちょっと、以下を見て練習してみてください。

慣れないうちは小数で表しても結構です。少しずつ分数で表せるようにしましょう。

(6)単位の変換

今回は、文字式でいろいろな表現をしました。
テストの文章題で問われてくる箇所ばかりですので、いっぺんにたくさん覚えることがあって大変ですが、コツコツ振り返り、繰り返し問題を解いて覚えていきましょう。