今回は方程式とは何か、そしてその解き方を勉強します。
前までにやってきた計算と方程式はルールが違います。そこを注意して見ていきましょう。
(1)方程式と解
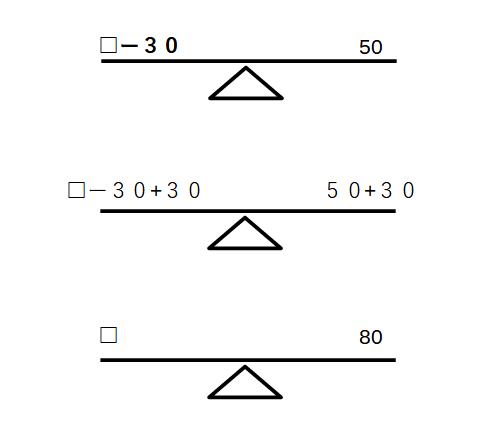
例) □ー30=50
□ー30+30=50+30
□=80
↓ 「□」を「x」に置き換える
x-30=50 →この式が「方程式」といいます
x-30+30=50+30
x=80 →これが「方程式の解」といいます
(2)方程式の解き方(基本)

さらに、問題を見ていきましょう。
①\( \displaystyle \frac { 5 }{ 3 } x = 10 \qquad \frac { 5 }{ 3 } x \) の係数 \( \displaystyle \frac { 5 }{ 3 } \) を消すために
\( \quad \displaystyle \frac { 5 }{ 3 } x \times \frac { 3 }{ 5 } = 10 \times \frac { 3 }{ 5 } \) \( \quad \) 両辺に \( \displaystyle \frac { 5 }{ 3 } \) の逆数 \( \displaystyle \frac { 3 }{ 5 } \) をかける
\( \quad x =6 \)
②\( 4x + 5 = 29 \)
\( \quad 4x + 5 -5 = 29-5 \qquad \) まずは両辺に -5
\( \quad \displaystyle \frac { 4 }{ 4 } x = \frac { 24 }{ 4 } \qquad \) 次に両辺に \( \displaystyle \frac { 1 }{ 4 } \) をかける
\( \quad x=6 \)
※移項
さて、これまでで方程式は両辺に同じものを+-×÷して解いていくものだということがわかりました。
しかし、式が複雑になれば、両辺に同じものを+-…とやっていては面倒、また、たくさんのことをやってミスが出てしまいやすくなります。
そこで、「移項(いこう)」ということをします。どういうものか見ていきましょう。

つまり、移項とは、両辺に同じものを+ー×÷、という行を飛ばして計算できるということです。=の反対側に消したい数値を符号を変えて移すことで、両辺に同じものを+ー×÷という過程を経ずに計算を進めることができるのです。
実際に、いくつか例を見てみましょう。
例)
① 3x=2x+8
3x-2x=8 「+2x」を符号を変えて左辺へ
x=8
②6x-11=4x+5 「ー11」を符号を変えて右辺へ
6x-4x=5+11 「+4x」を符号を変えて左辺へ
2x=16
③\( 8x = 4x + 8 \)
\( \quad 8x-4x = 8 \qquad \) 「4x」を符号を変えて左辺へ
\( \quad 4x =8 \qquad \) 係数(4)が残ってしまう!
\( \quad \displaystyle \frac { 4 }{ 4 }x = \frac { 8 }{ 4 } \qquad \) 両辺に \( \displaystyle \frac{ 1 }{ 4 } \) (4の逆数)をかける
\( \quad x=2\)
③のように、最後にxの係数が残った場合は、その係数の逆数を両辺にかけることによってxとなりますから、xの反対の辺に係数の逆数をかけてx=の形にします。
さて、今回は方程式の解き方について勉強しました。
正直言って、ここを見て「ふーん」となっただけでは絶対にできるようにならないので、なるべくたくさんの問題にあたって、しっかりと習得してください。