今回は方程式の文章題を勉強します。
定期テストや受験で直接関係してくるので、今までの方程式の計算をしっかりやった上で見ていきましょう。

文字に惑わされないよう注意!文字に慣れていきましょう。
(1)個数・代金
まずは例題を、上の板書の順番でやってみましょう。
例1)1個50円のリンゴをいくつかと、150円のかごを買ったら全部で750円でした。リンゴはいくつ買ったか?
①まず、わからない数(求めたい数)→この場合はリンゴの数=xと置く
→復習として、個数と代金の関係の式は
(代金)=(商品1つの値段)×(個数)
となります。
②文字式を作る→代金を式に
リンゴの値段→1個50円×x個=50x(円)
かごの値段→150円
代金は、15x+150(円)
③すると、リンゴとかごの合計が750円なので、「=」でつなげる!
15x+150=750
④方程式を解く!
50x=750-150
50x=600
x=12
⑤12個のリンゴを買った。→解答
例2)エンピツ7本と100円の消しゴム1個を買って、1000円出したらおつりは60円だった。エンピツ1本の値段は?
①わからない数(求めたい数)→エンピツ1本の値段=xとする。
②文字式を作る→代金を式に
エンピツ7本の値段→7x(円)
消しゴム1個→100(円)
代金は、7x+100(円)
③「1000円出したらおつりは60円」
→(出したお金)ー(代金)=(おつり)なので、
1000ー(7x+100)=60
④方程式を解く
1000-7xー100=60
ー7x=60-1000+100
ー7x=ー840
x=120
⑤エンピツ1本120円
例3)80円切手と50円切手を合わせて10枚買ったら代金が680円だった。80円切手は何枚買った?
①わからない数(求めたい数)→80円切手の枚数=x(枚)とする
※ちなみに、50円切手の枚数は(10-x)(枚)と表せる
80円切手 50円切手
1枚 10-1=9枚
2枚 10-2=8枚
x枚 (10-x)枚
②文字式を作る→代金を式に
80円切手の代金=80x(円)
50円切手の代金=50(10-x)(円)
代金は合わせて80x+50(10-x)(円)
③代金合計が680円なので
80x+50(10-x)=680
④方程式を解く
80x+500-50x=680
30x=180
x=6
⑤80円切手の枚数は6枚
※ちなみに、50円切手の枚数は?
x=6 ←これは80円切手の枚数
50円切手の枚数は(10-x)枚なので
10-6=4(枚)
(2)整数
例1)連続する3つの整数の和が42のとき、この3つの整数のうち1番小さい数は?
※復習~文字を使った式~
連続する3つの数
一番小さい数をnとすると、
n , n+1 , n+2 ←連続する3つの整数
①一番小さい数をxとする
→連続する3つの整数=x , x+1 , x+2
②「3つの和」を式に表す
→ x+(x+1)+(x+2)
③「3つの和が42」なので
→x+(x+1)+(x+2)=42
④方程式を解く
x+x+1+x+2=42
3x=39
x=13
⑤一番小さい数は13
例2)連続する3つの偶数の和が60のとき、これらの偶数のうち、中央の数は?
※復習~連続する3つの偶数
2n , 2n+2 , 2n+4
ちなみに、奇数は2n+1 , 2n+3 , 2n+5
①一番小さい数を2xとする
→連続する3つの偶数=2x , 2x+2 , 2x+4
②3つの和→2x+(2x+2)+(2x+4)
③和が60→2x+(2x+2)+(2x+4)=60
④方程式を解く
2x+2x+2+2x+4=60
6x=54
x=9
⑤一番小さい偶数は2×9=18
→ただ、問われているのは「真ん中の数」
(2x+2)のこと
代入→2×9+2=20 答えは20
(3)規則性
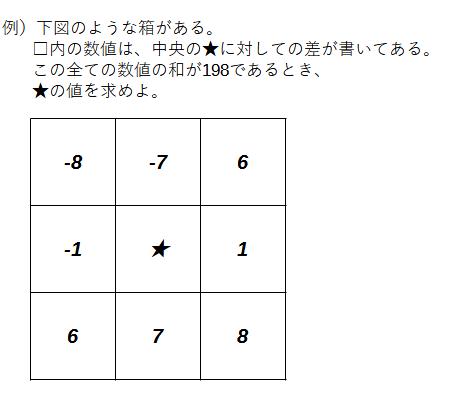
①中央の★をxと置くと、

の、ようになります。これならば、中央にどんな数が入ってもすべての□に数値を入れることができます
②「すべての数値の和が198」なので、
(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=198
③方程式を解く
x-8+x-7+x-6+x-1+x+x+1+x+6+x+7+x+8=198
9x=198
x=22 ∴中央の数→22
(4)図形
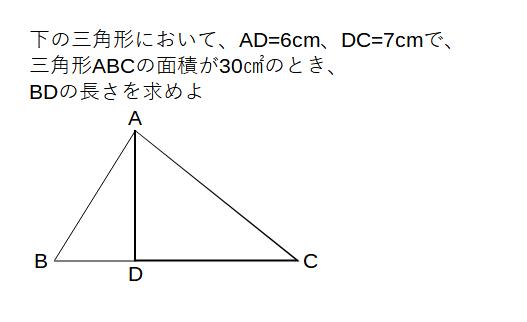
面積の公式に文字ごと当てはめて式を作り、計算する!
①BD=x(cm)とおく → 図に記入!
②BCの長さをxを用いて表す
→ \( ( x+7 )cm \) →三角形の公式に当てはめ
\( \displaystyle (x+7) \times 6 \times \frac { 1 }{ 2 } (cm^2) \)
③これが \( 30cm^2 \) なので
\( \displaystyle (x+7) \times 6 \times \frac { 1 }{ 2 } = 30 \)
④方程式を解く \(x=3 \)
⑤よって \( BD=3cm \)
わかっている情報は、なるべく図に書き込みましょう。
(5)過不足
例)みかんを何人かの子供にわけるのに、1人5個ずつわけると10個足りず、1人に4個ずつわけると2個余る。子供の人数とみかんの個数は?
①わからない数(求めたい数)→人数とみかんの個数
→文章題にはみかんの個数について書かれている
→人数をx(人)とおいて、みかんの個数についての式をつくる
②5個ずつわけると10個足りない
→x人に5個ずつわけると 5x(個)
→10足りないから 5x-10(個)
同様に、4個ずつわけると2個余る
→4x+2(個)
③上の2つの式を「=」で結ぶ
5x-10=4x+2
④方程式を解く
x=12
⑤人数は12人とわかる
みかんの個数については、
5x-10もしくは4x+2のどちらかにx=12を代入すれば求められる
4×12+2=50 50個
※安易に「余る=+」「足りない=ー」としない!下の問題の場合
例)「町内会費を1人400円ずつ集めると1000円余り、300円ずつ集めると500円不足する…」となった場合の式の立て方
人数=xとする
1人400円ずつ集めると1000円余る
→集めるはずの費用より1000円多くなる
→400x-1000(円)となる(+1000円ではない!)
1人300円ずつ集めると500円不足
→集めるはずの費用に足りない→足さないとダメ
→300x+500(円)となる
(6)速さ
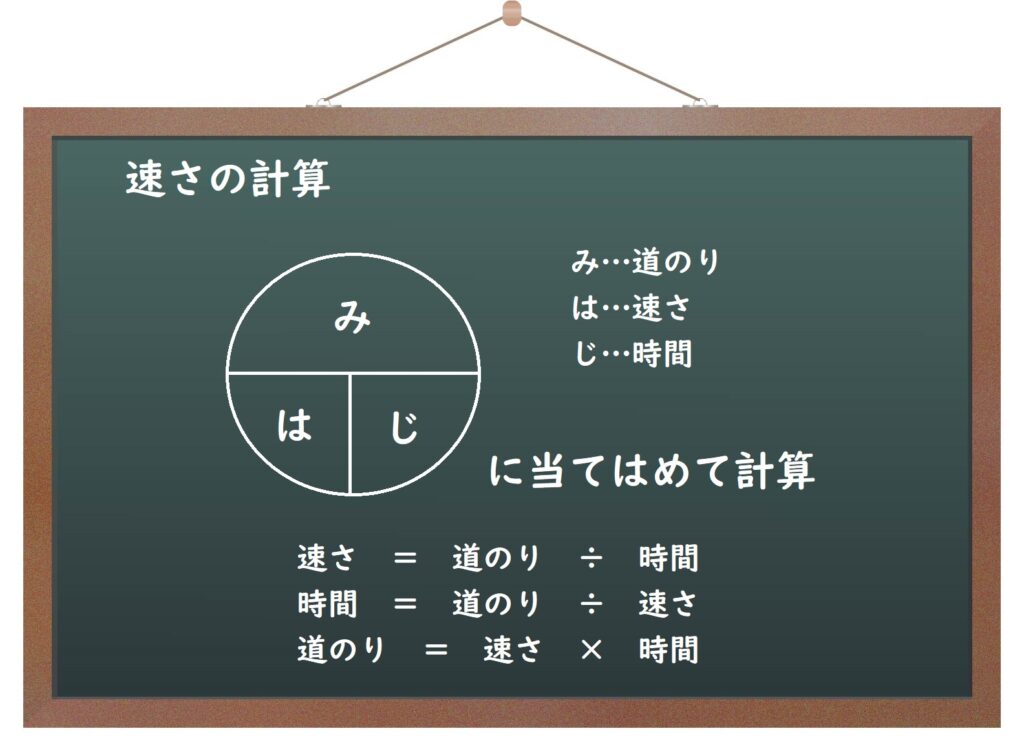
上の図を思い出し、図をきちんと書いて、公式に当てはめること!
「道のり」または「時間」で等式を作る!
(「速さ」では作らない!)
単位を合わせる!
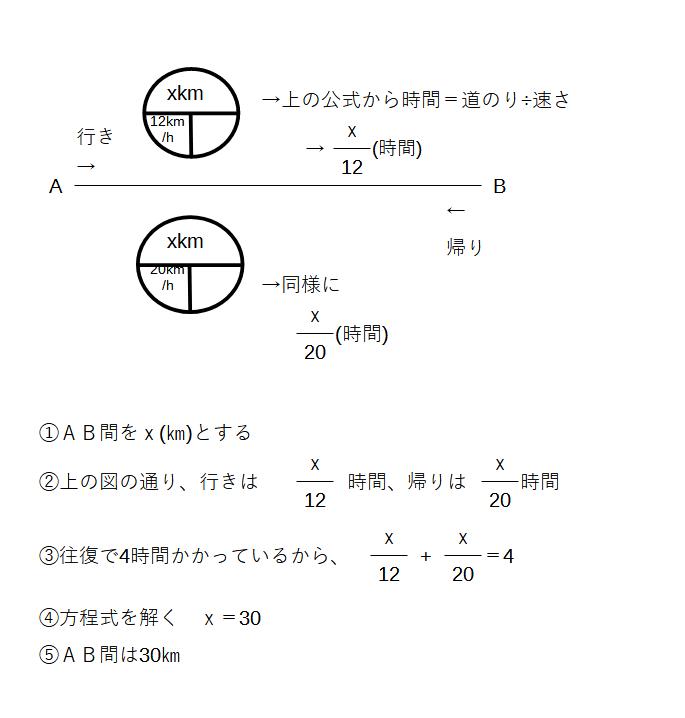
例1)A地点とB地点との間を、行きは時速12㎞、帰りは時速20㎞の速さで往復をしたら、4時間かかった。A,B間の道のりを求めよ。
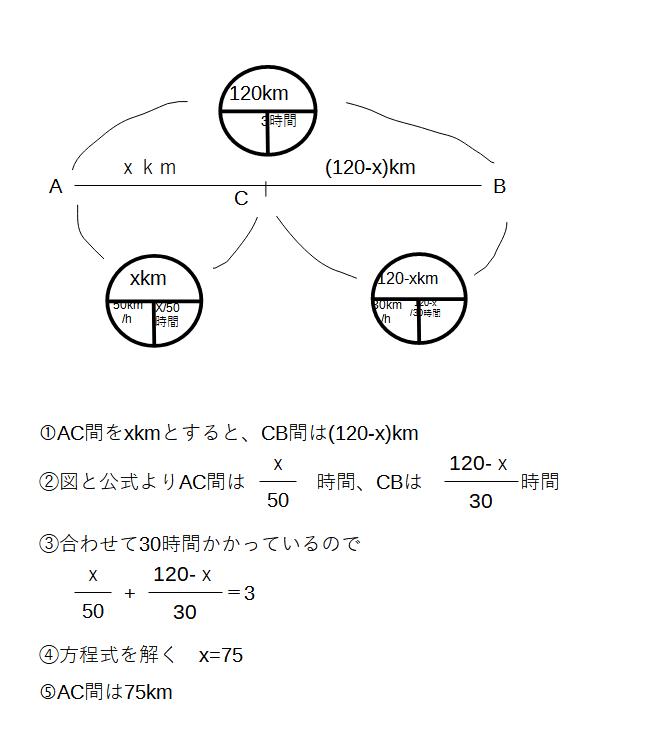
例2)A地点から120㎞離れたB地点まで行くのに、はじめは毎時50㎞の速さで進み、途中のC地点からは毎時30㎞の速さで進んだところ、ちょうど3時間かかった。AC間の道のりを求めよ。
速度が変わるパターンの問題です
例3)弟が駅に向かって家を出てから8分後に、兄が自転車で同じ道を追いかけた。弟の歩く速さを毎分80m、兄の自転車の速さを毎分240mとすると、あ人は家を出てから何分で弟に追いつくか。
追いつき問題です。
一見、ややこしいので、1つずつ確認をしながら見ていきます。
1.兄が弟に追いついた → 兄弟は家から同じ距離のところにいる
2.弟が家を出てから8分後に兄が出発 →兄が出発してからの時間をx(分)とすると、弟はその前に8分、毎分80mで移動している。
→弟の移動距離はその分も含めて計算する
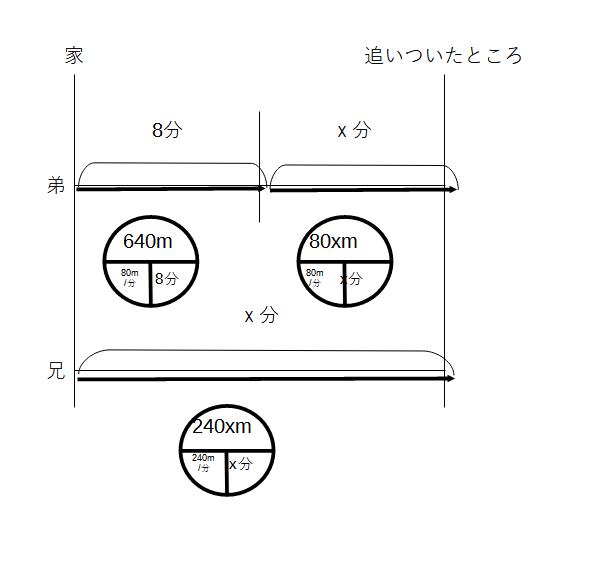
①兄が家を出発してから弟に追いつくまでの時間をx分とする
②上図のような距離の式ができる
③240x=80x+640
④ x=4
⑤4分
(7)割合

この割合の式を使って文字式をあてはめ、方程式を解きましょう
(小学校では割合は少数だったかもしれないけど、中学数学では分数を使うので、慣れていきましょう)
例)ある消費を定価の2割引で買ったら、代金は1600円だった。商品の定価は?
①定価をx(円)とすると、
②定価の2割引→ \( \displaystyle (定価) \times ( 1- \frac { 2 }{ 10 } ) = (定価) \times \frac { 8 }{ 10 } \)
つまり \( \displaystyle \frac { 8 }{ 10 } x \)
③これが1600円なので、
\( \displaystyle \frac { 8 }{ 10 }x = 1600 \)
④方程式を解く
\(x=2000 \)
⑤2000円
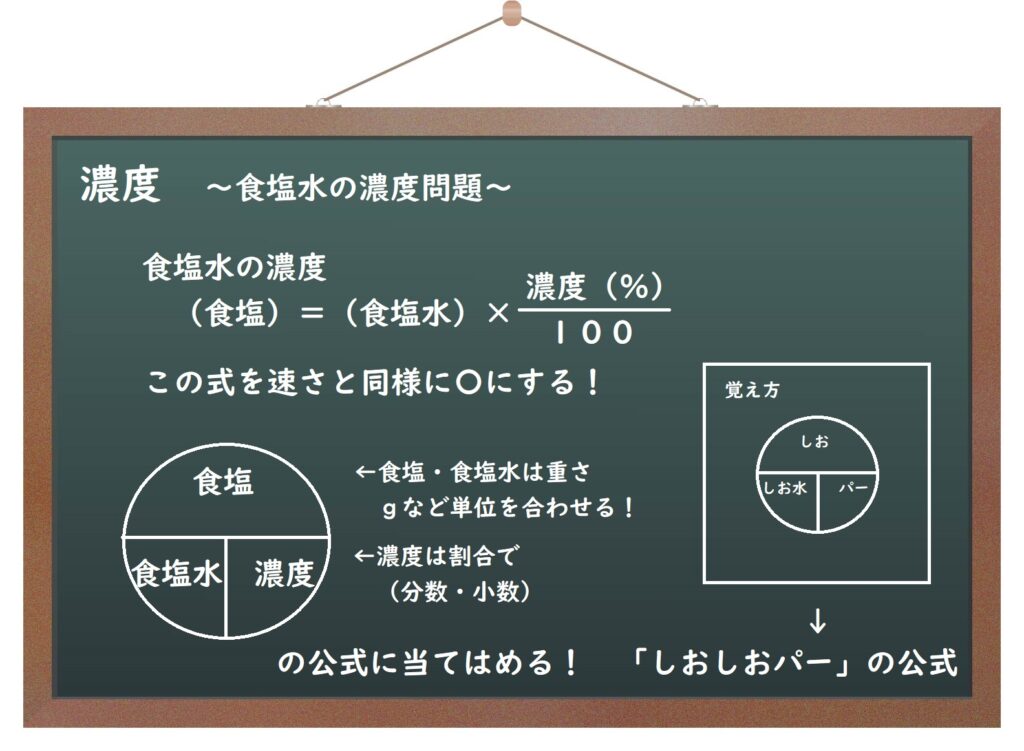
(8)濃度
例)8%の食塩水300gに3%の食塩水を加えて、7%の食塩水をつくりたい。3%の食塩水を何g加えればよい?

①3%の食塩水をxgとおく
②上の図のように、公式の円に当てはめる
③ \( \displaystyle 24x+ \frac { 3 }{ 100 }x = ( 300+x ) \times \frac { 7 }{ 100 } \)
④方程式を解く \( x=75 \)
⑤ \( 75g \)
今回は方程式の文章題の解き方について勉強しました。
あくまで典型的で基礎的な問題のみを取り上げていますので、ほかに問題集などを使って、いろいろなパターンを勉強して、たくさん問題を解くようにしましょう。
この単元はいろいろと問題を作りやすいので、テストでもよく出ます。
授業の振り返りとして、しっかり問題を解きましょう。