「高校受験数学」と銘打ったこの単元については、基本的に、今までのおさらいは中学のそれぞれの単元で行ってもらい、応用の部分を多く取り上げられたらと考えています。
まずは、方程式の応用からです。
(1)解が与えられた方程式

解答
「xの解が12」→「x=12のとき」と同じ意味
\( \displaystyle \frac{12-2a}{2} = a-12 \)
\( 12-2a =2a-24 \)
\( a=9\)
まず、\( \displaystyle 2x- \frac{1-x}{3}=-5 \) を解く! \(x=2\) となる
\( \displaystyle \frac{x-a}{3}= \frac{1}{2}x-a \)に代入 \( \displaystyle a=-\frac{1}{2} \)
(2)代金
問)2000円でケーキを3個、120円のシュークリーム6個買ったら、おつりは230円であった。ケーキ1個の値段を求めよ。
文章題の解答手順(振り返りです)
①わからないものをxと置く
②xで表せるものを考える
③方程式をたてる
代金…合計代金を考える
解)
ケーキ1個…x円 とおく
ケーキ3個…3x円
合計…3x+120×6
(ケーキ)+(シュークリーム)
2000-(3x+720)=230
2000-3x-720=230
-3x=-1050
x=350
(3)過不足
問)紙を1人3枚ずつ配ると36枚余り、1人5枚ずつ配ると20枚足りない。人数と紙の枚数を求めよ。
解答手順
1人~…人数をx
1グループ~…グループ数をx
●1~…~をxとおく
※式が2つできる!
解)人数をxとすると、紙の枚数は、
①3x+36 「3枚ずつ配ると36余る」
②5x-20 「5枚ずつ配ると36足りない」
3x+36=5x-20
-2x=-56
x=28
(4)速さ
問)A,B地点を往復するのに、行きは20km/時、帰りは60km/時の速さで進んだら、合計で2時間40分かかった。AB間の道のりを求めよ。
速さのおさらい
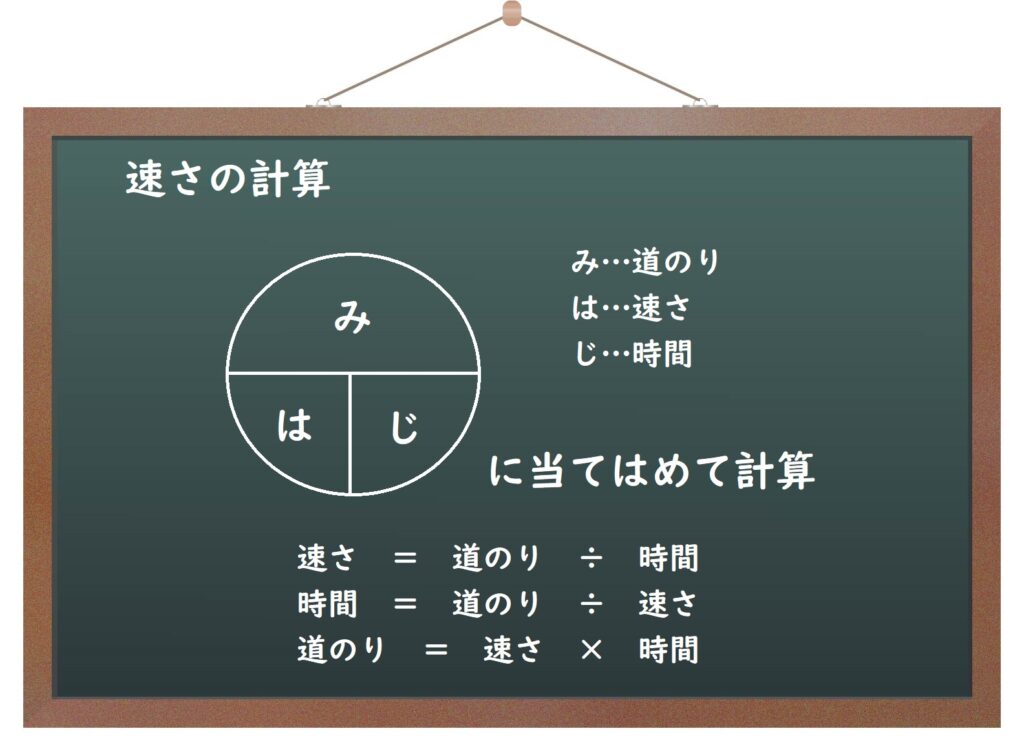
上の計算を振り返り、頭に入れて、次の図

解)上の図に当てはめて解く
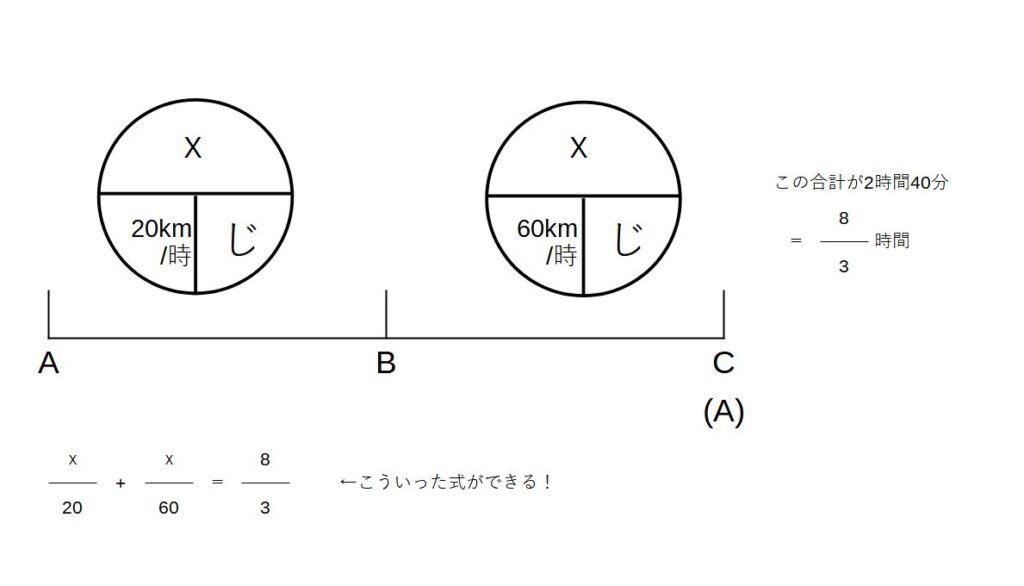
あとは式を解くだけ
3x+x=160
4x=160
x=40 A.40km
(5)割合
問)定価の3割引きに消費税5%を加えたら、定価より636円安くなった。定価を求めよ。
割合の表し方(振り返り)

解)
定価をxとすると
xの3割引 \( \displaystyle x \times (1- \frac{3}{10} ) = \frac{7}{10} x \)
消費税5%増 \( \displaystyle \frac{7}{10} x \times (1+ \frac{5}{100} ) \)
\( \displaystyle \frac{7}{10}x \times (1+ \frac{5}{100} )=x-636 \)
\( \displaystyle \frac{7}{10}x \times \frac{105}{100}x -x=-636 \)
\( \displaystyle ( \frac{147}{200}- \frac{200}{200} )x=-636 \)
\( \displaystyle -\frac{53}{200} x=-636 \)
\( \displaystyle x=636 \times \frac{200}{53} \)
\( x=2400 \)
今回は1次方程式の応用(文章題)についてふりかえり(おさらい)しました。
基本的な計算は省いてますので、わからないことができたらそのつど、ふりかえり学習するようにしましょう。たくさん問題を解いてください。