今回は連立方程式の応用です。
問題文→式の立て方が重要になってきますので、典型問題を自分で解いてみて、パターンを覚えていきましょう。
(1)代金
例)100円と50円が何枚かずつあり、合計で5400円ある。また、50円をすべて10円に両替すると、100円、10円合わせて162枚だった。100円玉と50円玉それぞれ何枚ずつあったか求めよ。
※求めるもの2つ→x、yと置く。
文字を2つおいたら、式を2つたてる
この場合、100円の枚数=x枚、50円の枚数=y枚とおく。
式を2つ立てる
100x+50y=5400 → 金額
10円の枚数は、50円の5倍なので、5y枚
x+5y=162 → 枚数
式が2つ立てられたので、連立方程式で解く
\( \begin{cases}100x+50=5400…① \\ x+5y=162…② \end{cases} \)
\( \begin{array}{rr}
& 100x+50=5400\\
-\big{)}&10x+50y=1620\\
\hline
&90x=3780\\
&x=42\\
&y=24
\end{array}\)
A.100円42枚、50円24枚
(2)~けたの数
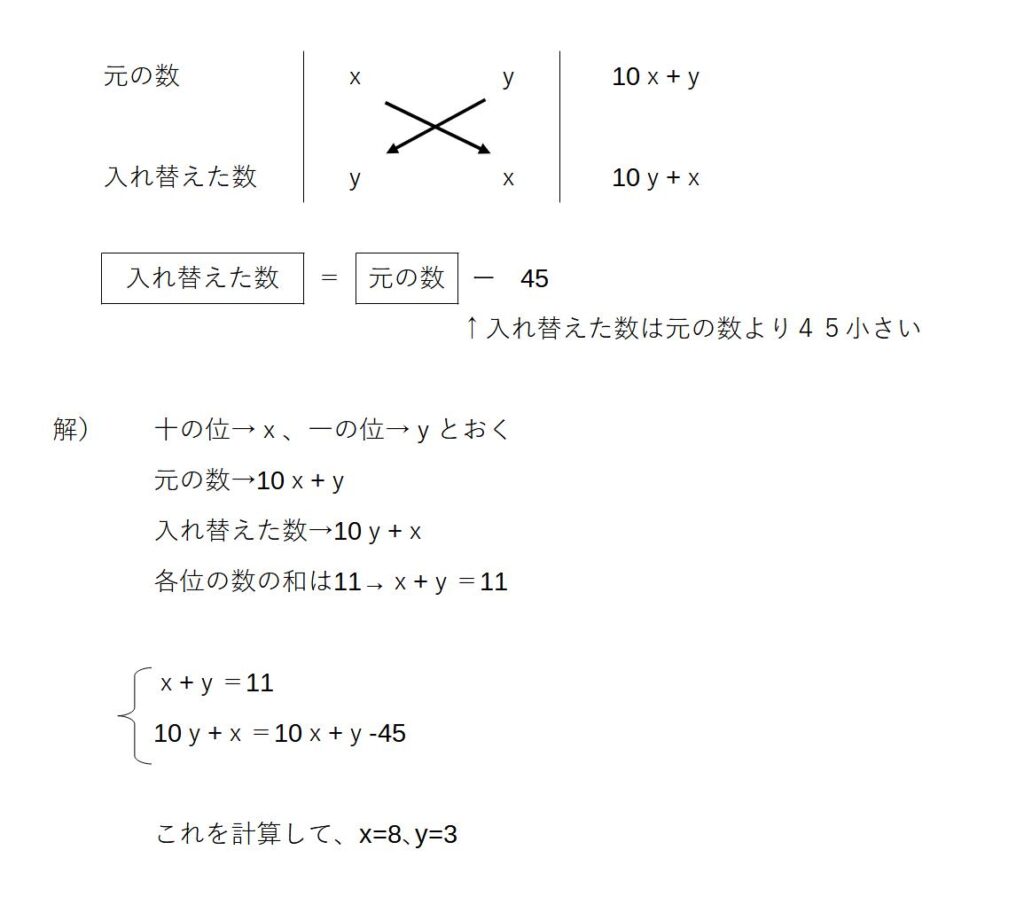
例)2けたの正の整数がある。各位の数の和は11で十の位と一の位の数を入れ替えると元の数より45小さくなる。元の数を求めよ。
※2桁の数の表し方
10a+b
3桁の場合→100a+10b+c
4桁の場合→1000a+100b+10c+d
(3)増減
例)先月の会議室の利用者は、男女合わせて535人であった。今月は先月に比べて男子が10%減り、女子が20%増えたので合計で576人になった。今月の男子、女子の人数を求めよ。
※昨年の人数を文字でおく。求めてから今年の値を求める。
←式を解いてからひと手間かかるので注意!!
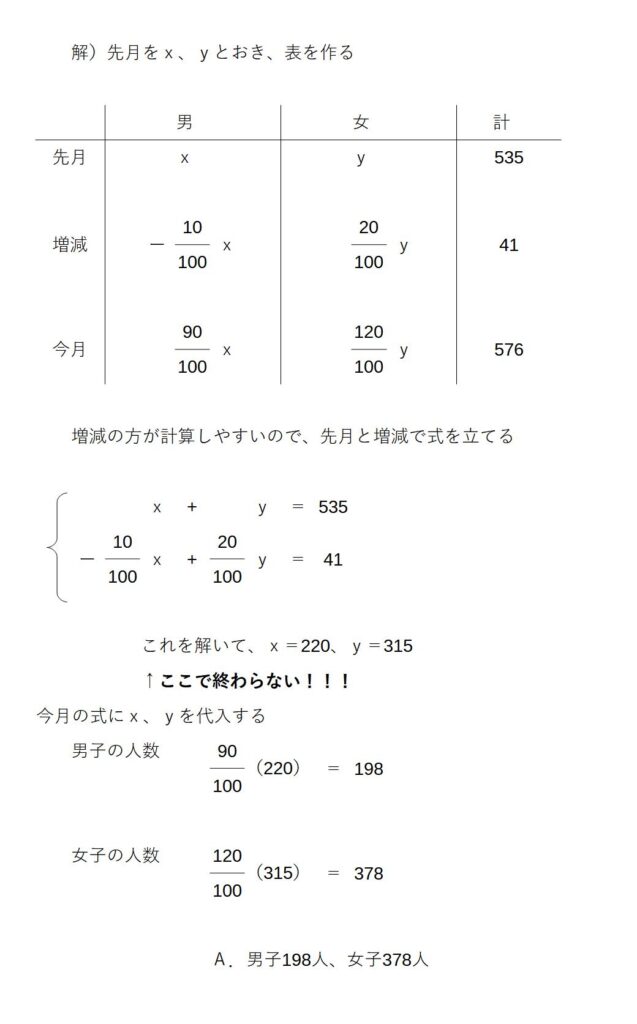
この問題の注意点は、連立方程式を解いた時点で、うっかり満足して答えをこれだ!として解答してしまうことです。
この問題はあくまで、「今月の」人数を求めなければならないので、連立方程式の解からさらに計算を行う必要があります。
今回は連立方程式の応用として、問題文の解き方を勉強しました。
連立方程式の解き方については、しっかりその単元でふりかえり学習を行ったうえで、問題文から式へ立て方をしっかり覚えてください。