今回は一次関数になります。
早速行きましょう。
一次関数の問題も、比例反比例の問題同様、式で表して数を代入する、といった手順でやっていきます。
一定の問題パターンが存在しますので、解き方をふりかえり学習し、何度も復習して覚えていきましょう。
(1)式を求める

問y=4x-1に並行で、(2,3)を通る直線の式を求めよ。
※平行ということは、傾きが同じである→今回は4xであることは確定
ちなみに、垂直である場合→傾きをかけるとー1
解)傾きが同じなので、
y=4x+bとなる
ここへ(2,3)を代入
3=4×2+b
b=ー5 y=4x-5
(2)グラフと交点
グラフの好転の座標を求めるタイプの問題です。
※交点 → 連立させて解いた解になる
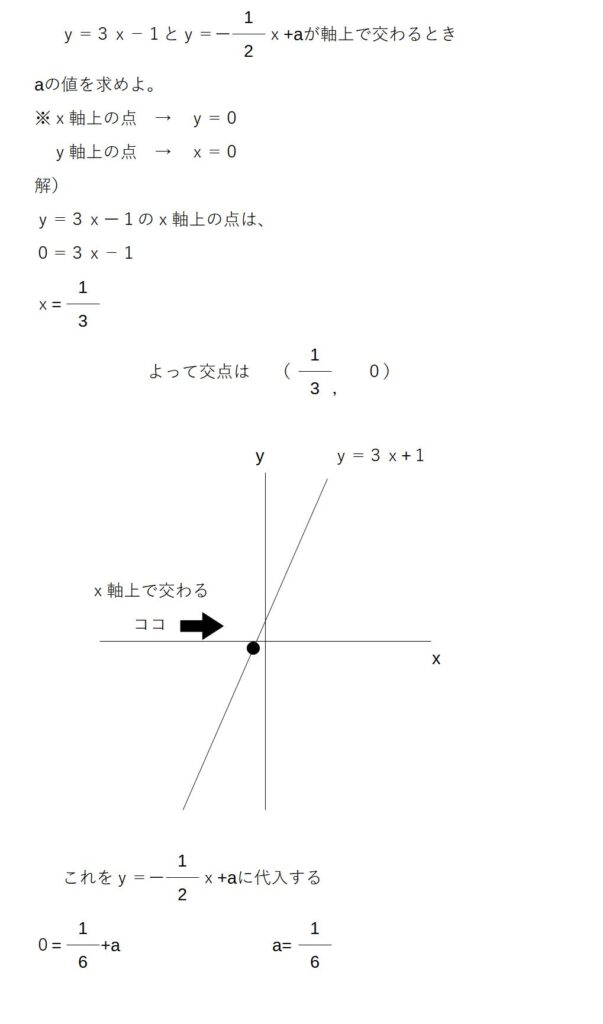
例1)y=ー2x-4とy=3x+1の交点を求めよ。
解1)y=ー2x-4
y=3x+1 の連立方程式を解く
ー2x-4=3x+1
ー5x=5
x=ー1
y=ー2 (ー1,ー2)
例2)
例3)点(1,3)、(4,12)を通る直線の式を求めよ。
※それぞれの点を、y=ax+bの式に代入し、連立方程式をつくる!
解3)y=ax+bと置く
(1,3)より3=a+b
(4,12)より12=4a+b
この2つの式を連立方程式にして、計算をする
a=3,b=0 A. y=3x
(3)変化の割合
変化の割合については、結構忘れがちなのに、使う場面がおおいので、ここでもう一度おさらいして思い出して、使えるようになりましょう。
例)一次関数y=5x+10において、xの値がー3から2まで増加するときのyの増加量を求めよ。
※傾きが5→変化の割合
\( \displaystyle 変化の割合=\frac{yの増加量}{xの増加量} \)
解)yの増加量をaとおく
\( \displaystyle 5= \frac{a}{2-(-a)} \)
\(a=25 \)
(4)座標平面上の面積
例)△OAB、△OBCの面積を求めよ。
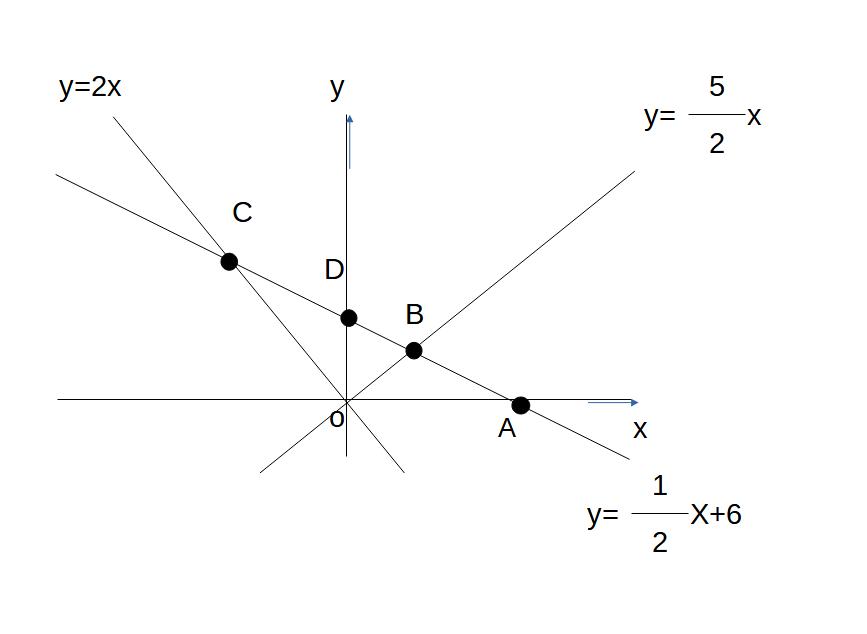
※まずは、すべての点(ABCD)について、座標を出す。
→AとDについては、それぞれx軸、y軸との交点なので、Aはy=0を代入、Dはx=0を式に代入する。
BとCについては、2つの直線の式の交点、つまり連立方程式の解が座標になる
計算すると、A(12,0)B(2,5)C(-4,8)D(0.6)となる。
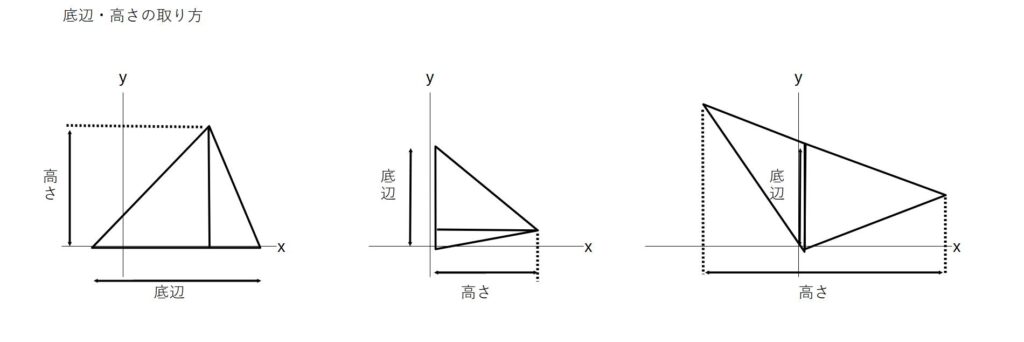
上図のように三角形の底辺と高さを必要な座標からとる
\( \displaystyle △OAB=12 \times 5 \times \frac{1}{2} = 30 \)
\( \displaystyle △OBC=6 \times 6 \times \frac{1}{2} = 18 \)
また、下図のような方法でも求めることができます。
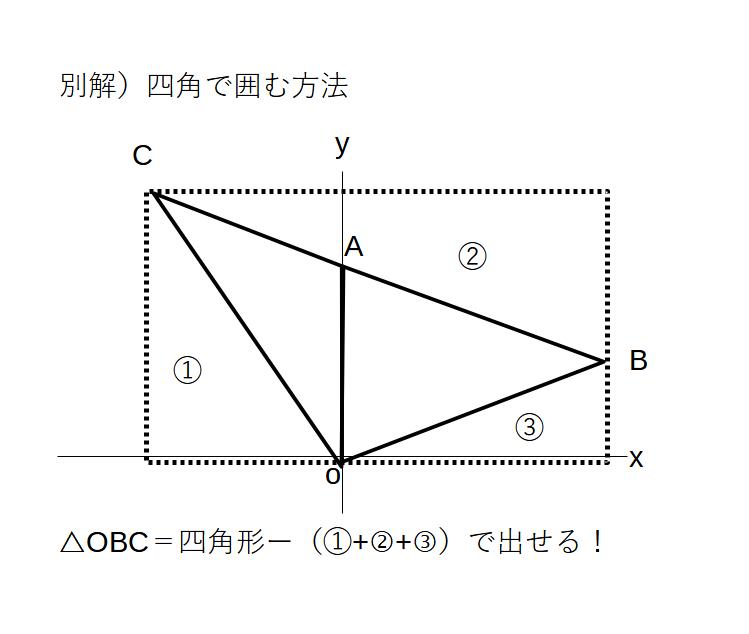
また、この三角形にかんして、ちょっとだけ早く解ける公式を紹介します。
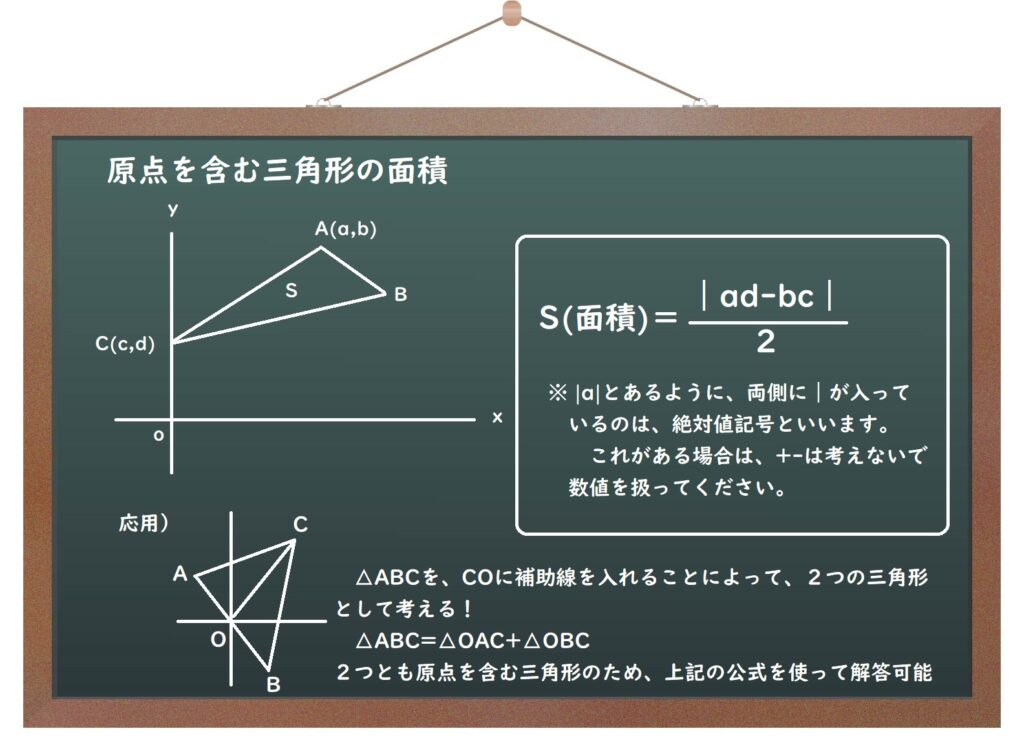
(5)座標平面上の長さ
例)AB,BCそれぞれの長さを求めよ。
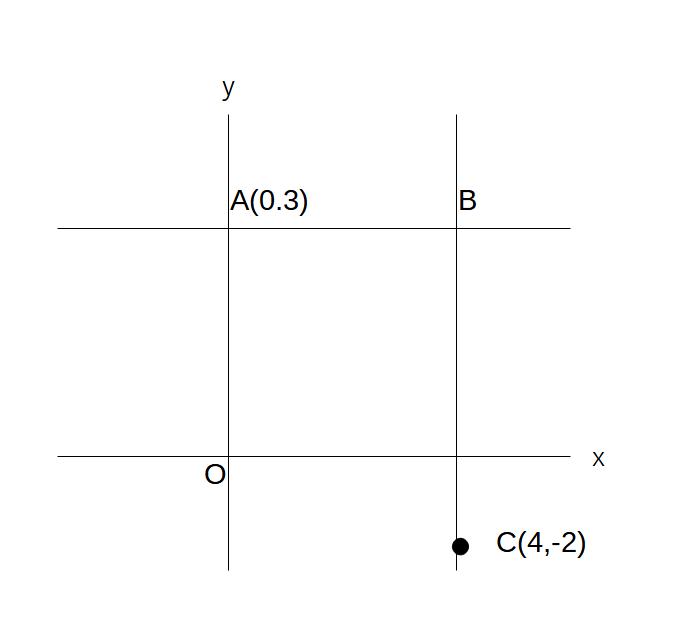
※縦の長さ→yで
横の長さ→xで測る
長さの求め方 → 大きい座標ー小さい座標
解)B(4,3)※縦が同じ→xが同じ
横が同じ→yが同じ
AB=3-0=3
BC=3-(ー2)=5
次は、ちょっと発展版です。
例)PQの長さを求めよ。
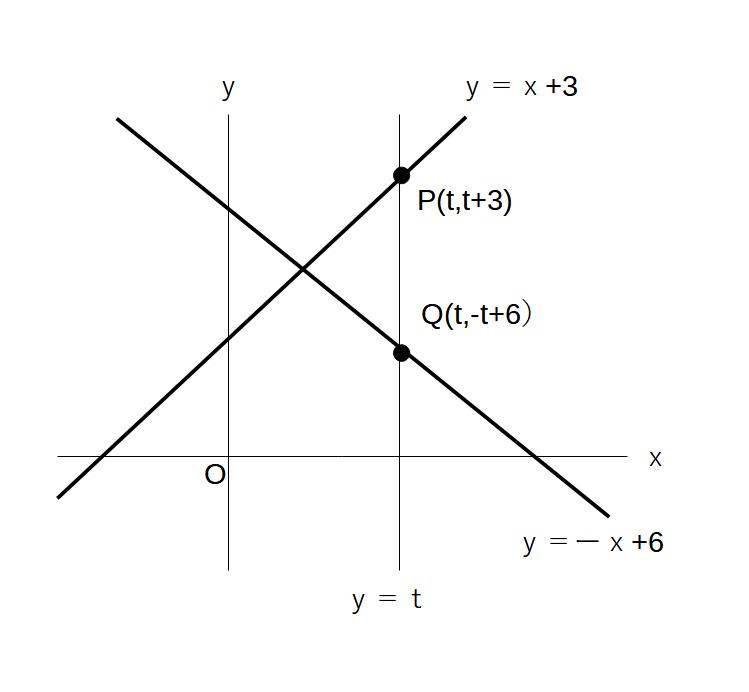
文字で座標が書かれていますので、ちょっとややこしく感じるかもしれませんが、やり方は一緒です。
PQ=PのyーQのy
=(t+3)ー(ーt+6) → PQ=2t-3
(6)応用
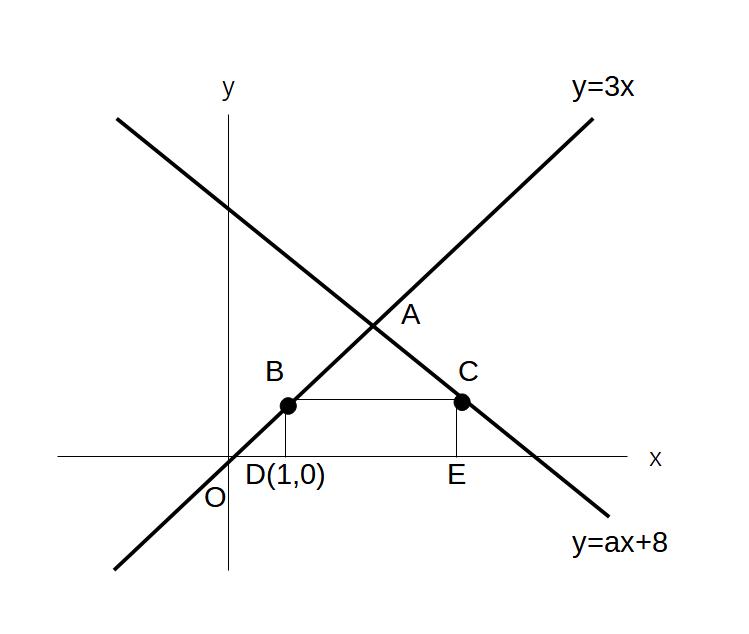
a<0のとき、次の問いに答えよ。
(1)OAが(b、ー12)をとおるときのbの値
(2)a=ー3のときのAの座標
(3)BDEC=12の時のの値
※わかる座標を計算等して出す
わからない座標は文字をおく

(7)ダイヤグラム
例)Aさんが家を出発し、20分で1.4㎞先の学校に着いた。12分~20分の速さが100m/分のとき、問に答えよ。
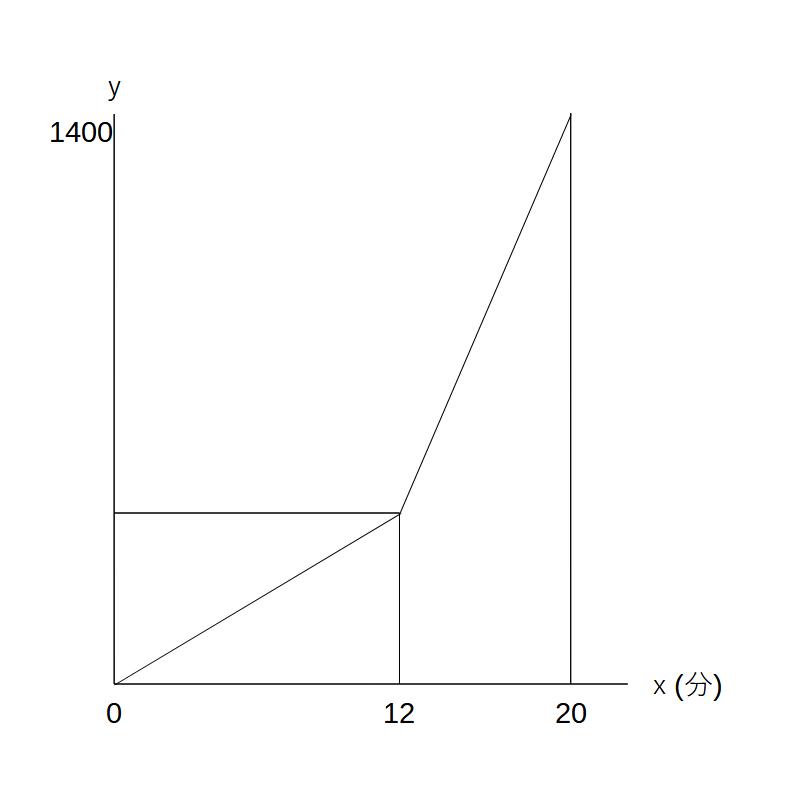
(1)12分のとき何mの地点にいるか。
(2)0~12分間の速さは何m/分か。
※グラフが曲がる → 別の式になる
始点終点が変化する点の座標を出す
x軸が時間、y軸が距離なので、傾きが速さになる
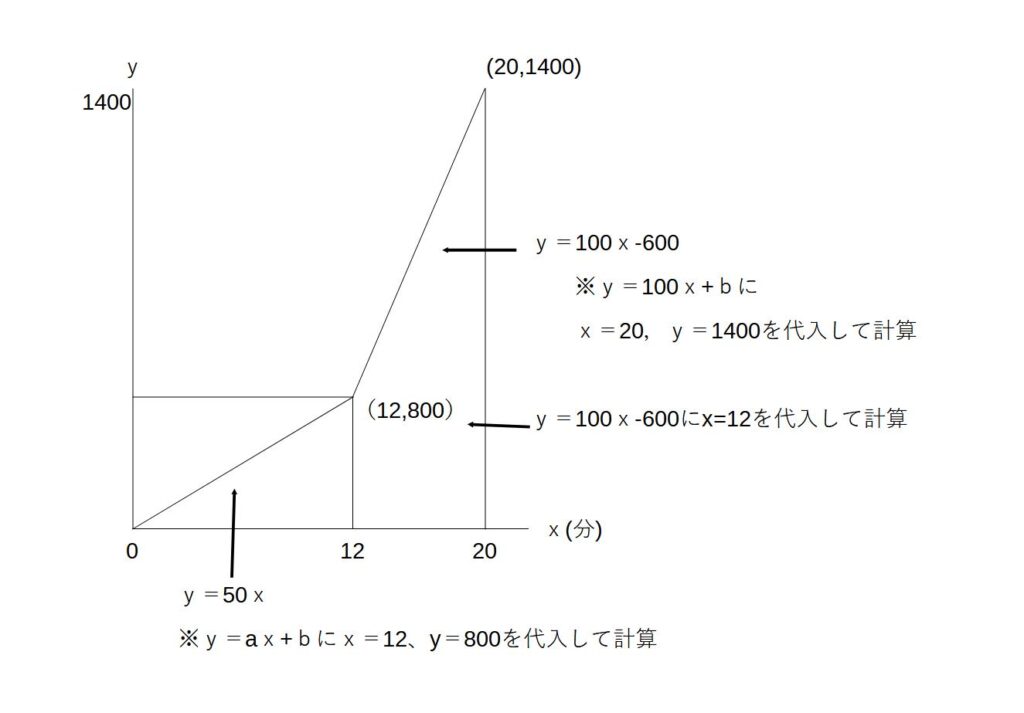
解)
(1)(12,800)より、800m
(2)y=50xより、50m/分
今回は一次関数の文章題を勉強しました。
基本的なことを覚えていないと全く答えられないので、これを機会にしっかりふりかえり学習を行い、身につけましょう。
ちなみに、ほかにも水量の問題やパラメータの問題など、紹介できていない典型的な問題もありますので、問題集などで保管するようにしてください。
こちらでも随時、問題を更新予定です。