今回は比例のグラフについて勉強します。
比例の特徴をよく理解し、問題の解き方を覚えていきましょう。
(1)比例の特徴
まず、比例とはどういったものなのかを見てみましょう。
例)y=2x
表にすると…

xが大きく(小さく)なるにつれ、yもともなって大きく(小さく)変化することになります。
(2)比例のグラフ
次に、比例のグラフを見ていきます。
例)
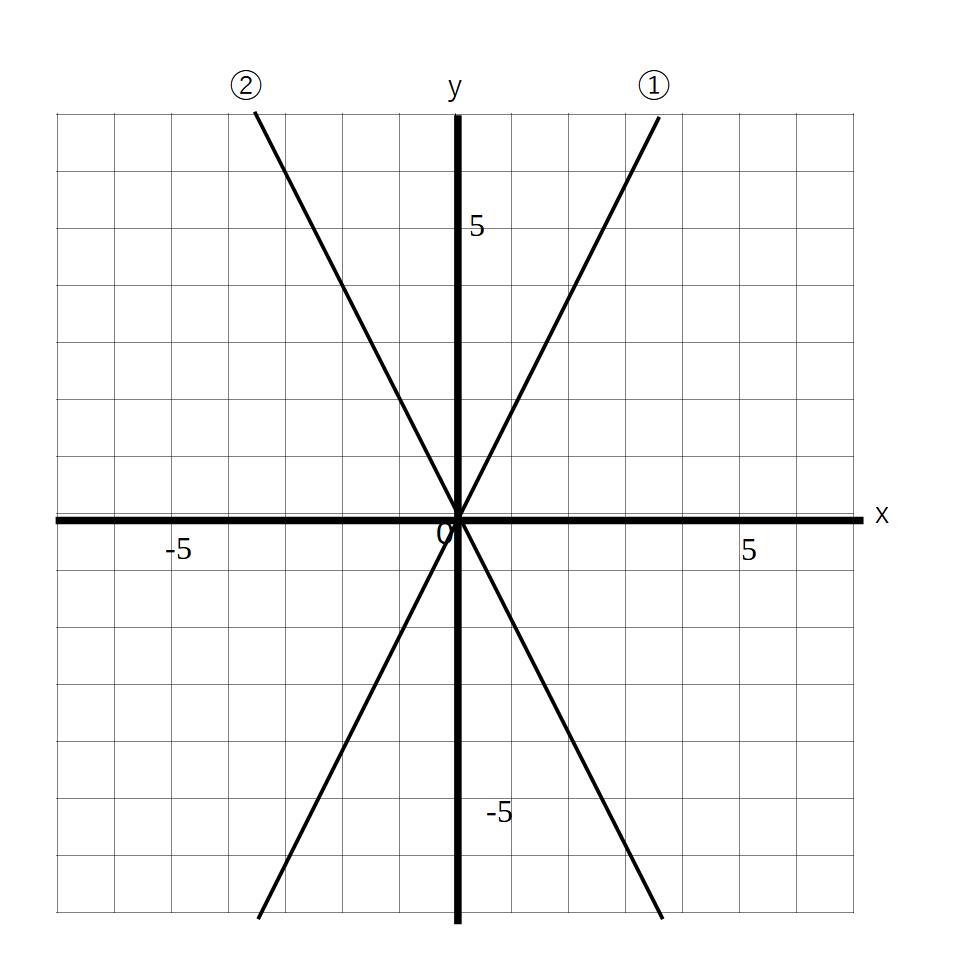
①y=2xのグラフ
②y=ー2xのグラフ
表にすると…

上の図のようになります。さらにここから細かい点を取っていき、すべての点をつなげれば直線になる!
→それが比例のグラフです
一度、比例のグラフの特徴をまとめておきます。

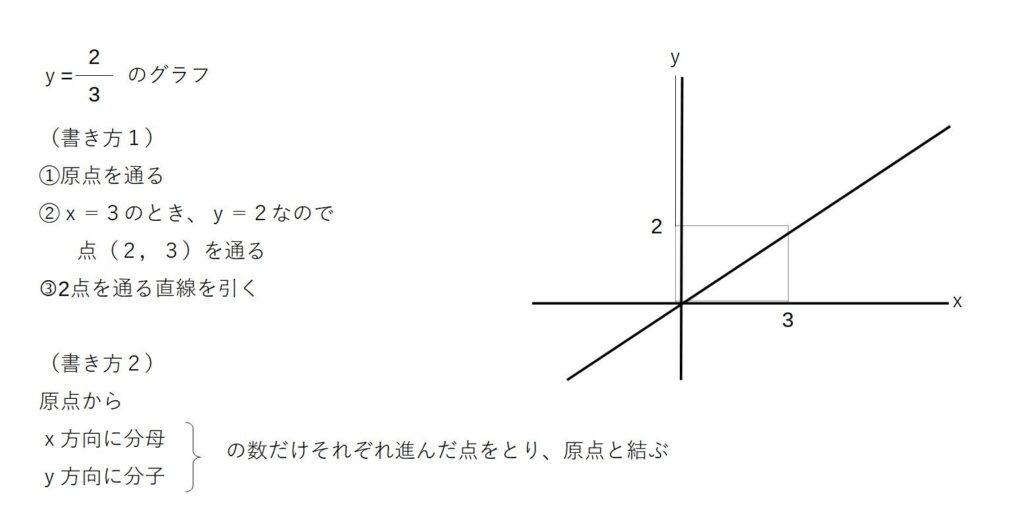
(3)比例のグラフの書き方
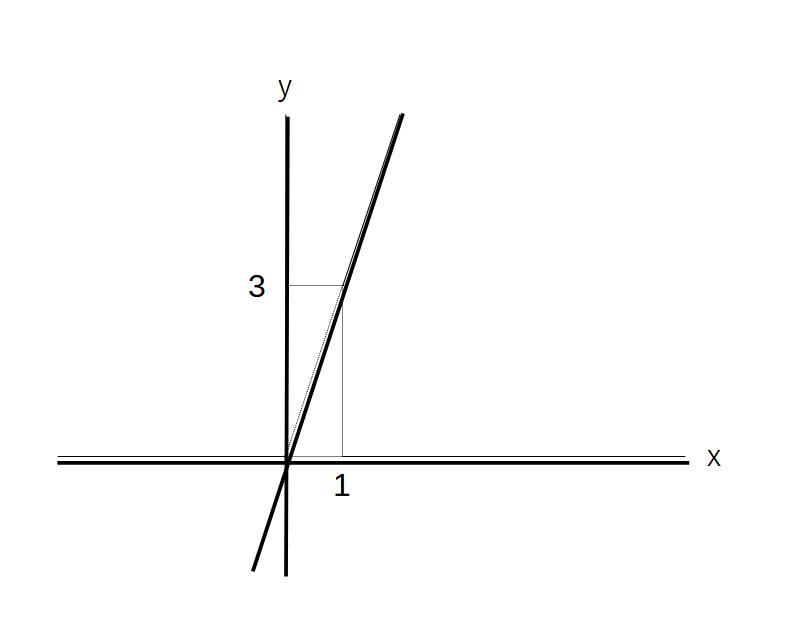
例1)y=3xのグラフ
①比例の線は原点を通る
②x=1のとき、y=3なので点(1,3)を通る
③2点を通る直線を引く
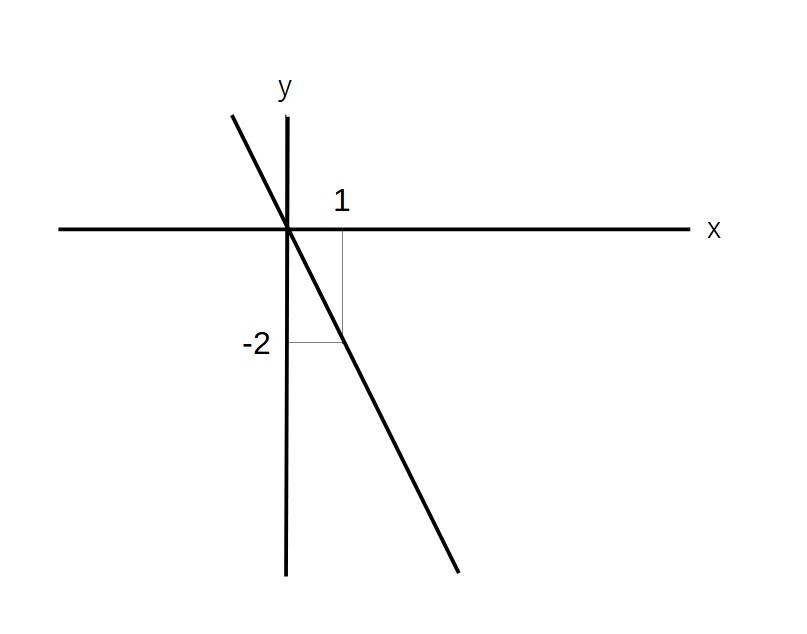
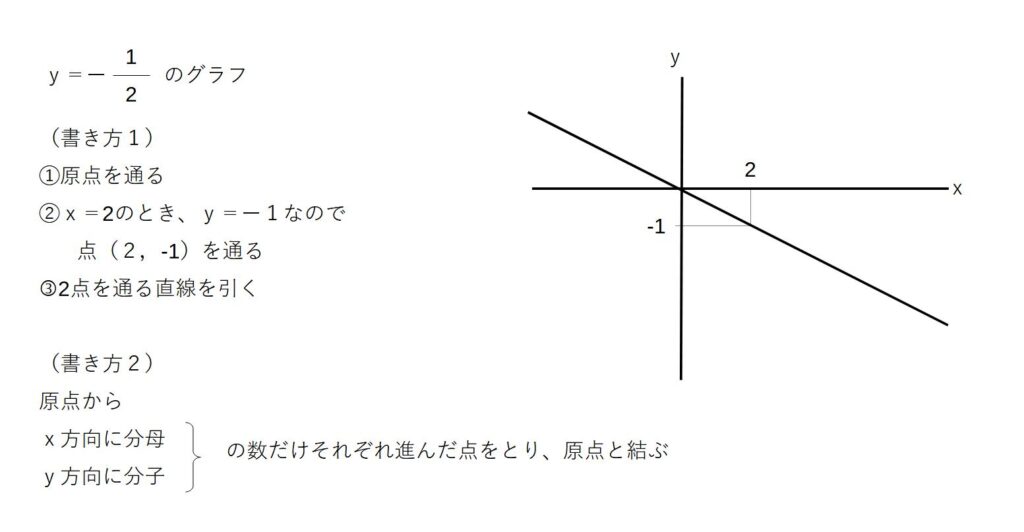
例2)y=ー2xのグラフ
①原点を通る
②x=1のとき、y=-2なので点(1、-2)を通る
③2点を通る直線を引く
例3)
例4)

グラフと実際に書いて練習してみましょう。
比例定数の言葉のところは、テストの問題文で聞かれたときに、「どういった意味だっけ?」とならないように今のうちに同じ意味の言葉は覚えておきましょう。
(4)グラフから比例の式を求める
例)グラフの式を求めよ。
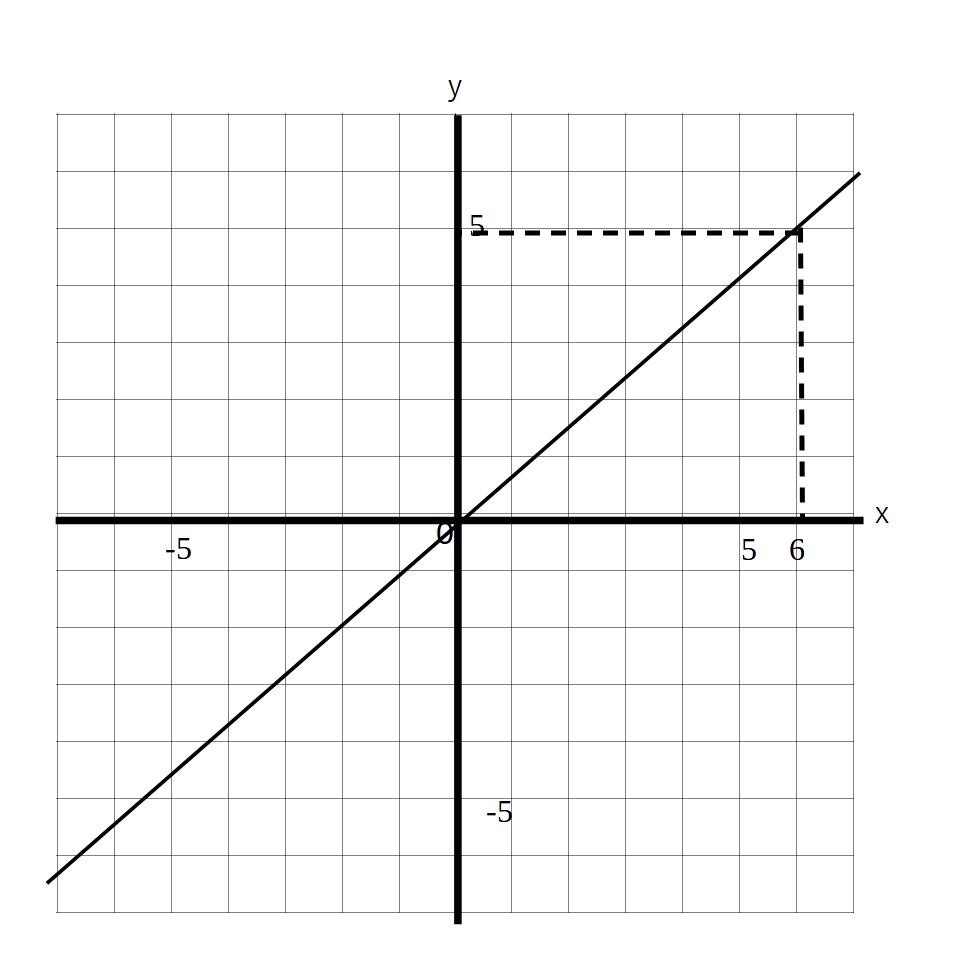
※グラフが通る点をみつけて、y=axに代入する!
通る点は(6,5)
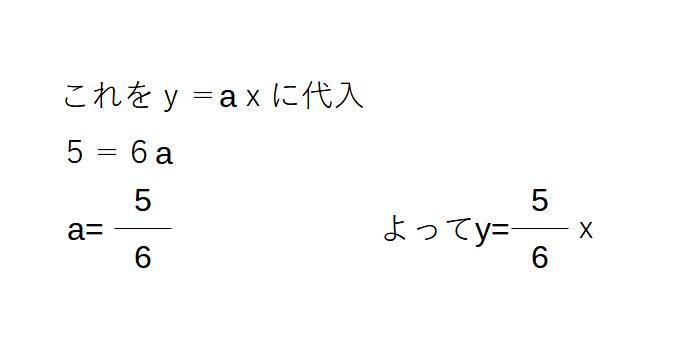
自分でグラフから点の数値を読み取り、それを比例の式に代入する、という一連の作業をできるようになりましょう。
(5)変域とグラフ
例1)y=2x(ー2≦x≦3)のグラフを書け。
※これは、y=2のグラフで、xがー2から3までの間の部分だけグラフにかけ、という問題です。
y=2xにx=ー2を代入するとy=ー4
x=3を代入するとy=6
つまり、y=ー2xのグラフの中で、
-2≦x≦3 -4≦y≦6の範囲にグラフを書きこむ
そうすると、下のようになる
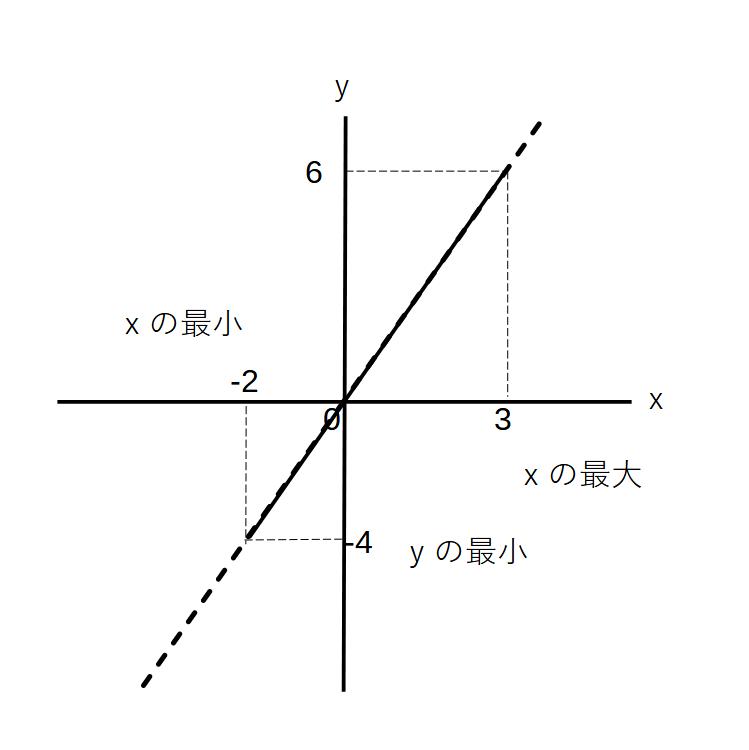
例2)下図のような長方形ABCDで、点Pは辺BC上をBからCまで動く。
BPの長さをx、⊿ABPの面積をy㎠とするとき、
①yをxの式で表せ
②xの変域を求めよ。
③xとyの関係を表すグラフを書き、yの変域を求めよ。
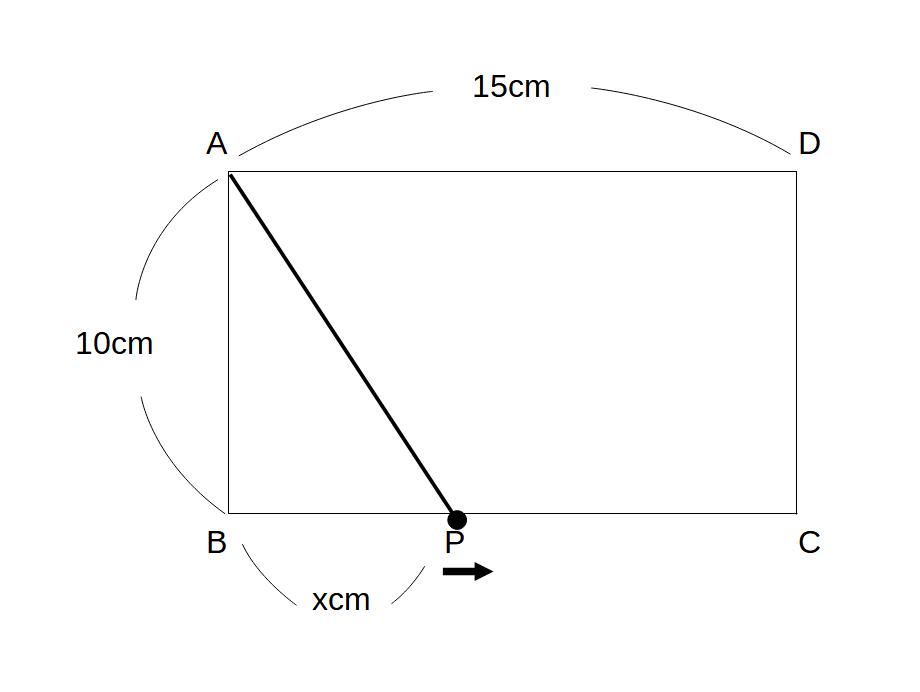
テストによく出る問題です。初めて見たらややこしそうで混乱するかもしれないですが、解説を見ればわかるはずです。わかったら同じような問題を何度も解きましょう。

(6)比例定数の範囲
例)y=axのグラフが線分AB(A(1,5)B(4,2))と交わるとき、aの値の範囲を求めよ。
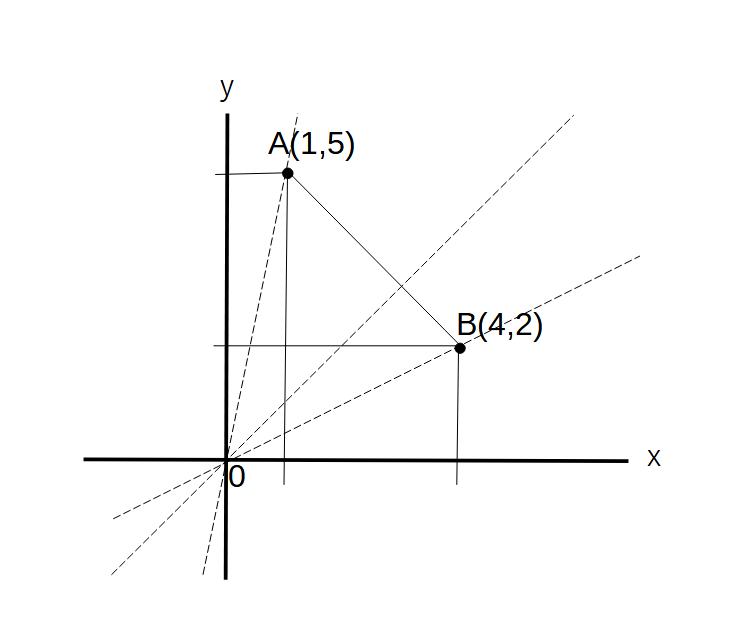
上の図のグラフを見てもらえばわかる通り、aの値によってAからBの範囲でグラフが変化することがわかります。
線分の両端AとBがそれぞれの最大最小になりますから、このAとBの座標をそれぞれ代入して、aの値を求める
→2つのaの値が、条件を満たすaの最大、最小値になる

今回は比例の式について勉強しました。
いろいろな問題が出てきて大変ですが、まずは言葉の意味だけでも覚えるようにしましょう。