比例と反比例の利用～文章題～

例１）16Lまで入る空の容器に毎分４Lの割合で水を入れるとき、入れ始めてｘ分後の水の量をｙＬとする。このとき、

①ｙをｘの式で表せ

②ｘの変域を求めよ

③ｘとｙのグラフをかけ

④水の量が12Lとなるのは何分後か

解1）

①毎分４Ｌ　→　1分後なら４×１＝４Ｌ

　　　　　　　　２分後なら４×２＝８Ｌ

　　　　　　　　４分後なら４×４＝16L

つまり、比例の式になる！　　ｙ＝４ｘ

②容器は16Lまでしか入らない→ｙ（水の量）は16までしかない

つまり、ｙの変域は０≦ｙ≦１６　←これをｙ＝４ｘに代入して計算

ｘの変域は０≦ｘ≦４

③グラフはｙ＝４ｘで０≦ｘ≦４（０≦ｙ≦16）

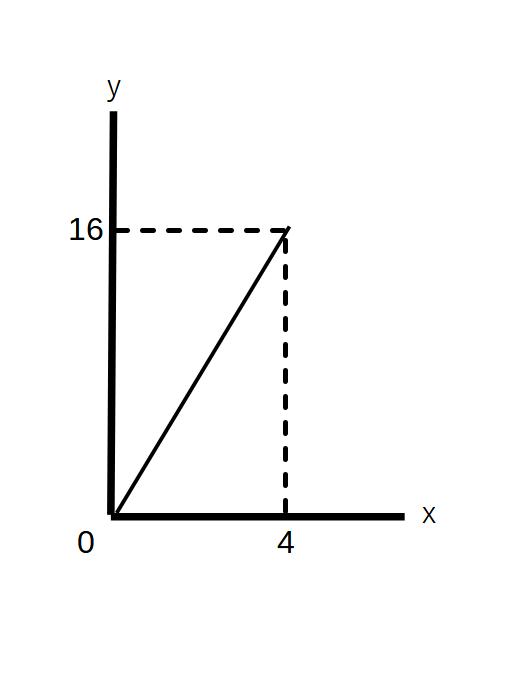
④水の量が12L　→　ｙ＝１２ということ

ｙ＝４ｘにy=12を代入

１２＝４ｘ　　　ｘ＝３　　Ａ．3分後

例2）A地点から20km離れたB地点まで、時速4kmで歩いた。ｘ時間で歩いた距離をｙｋｍとする。このとき、

①ｙをｘの式で表せ

②ｘとｙの関係を表すグラフをかけ

③6㎞地点を通るのは、歩き始めてから何時間後か

※どの単元でも出てくる速さの問題ですが、例によって図に表してみれば解けます。

解2）

①図に表します

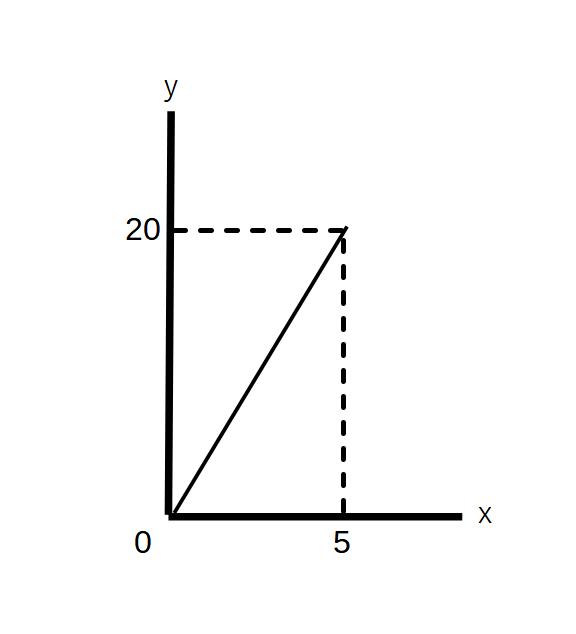
となるので、ｙ＝４ｘ

②０≦ｙ≦20　20㎞地点には20＝４ｘ　ｘ＝５

→5時間後に到着　０≦ｘ≦５　よって

例3）家から学校まで、毎分100mの速さで歩くと30分かかる。この道のりを毎分ｘｍの速さで進んだとき、かかる時間をｙ分とする。このとき、

①ｙをｘの式で表せ

②この道のりを毎分60mの速さで歩くと学校まで何分かかるか

③かかる時間が15分のとき、進む速さを求めよ

解3）

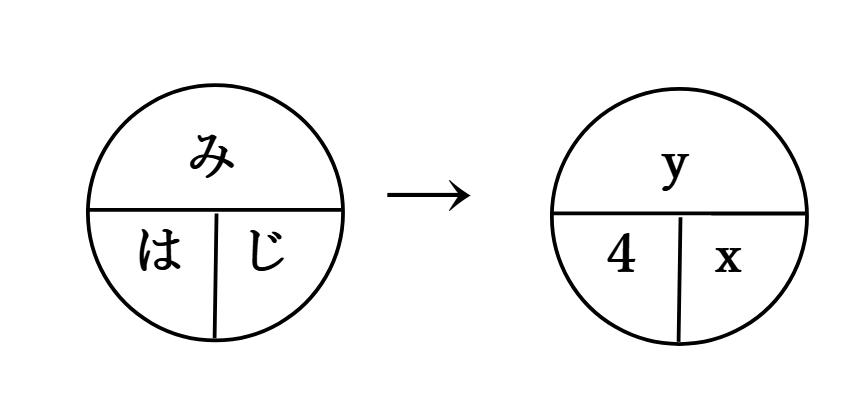
①まず速さの公式に当てはめていく

では道のりは？

→問題文より「毎分100mなら30分」

「は」×「じ」なので、100×30＝3000ｍ

よって、

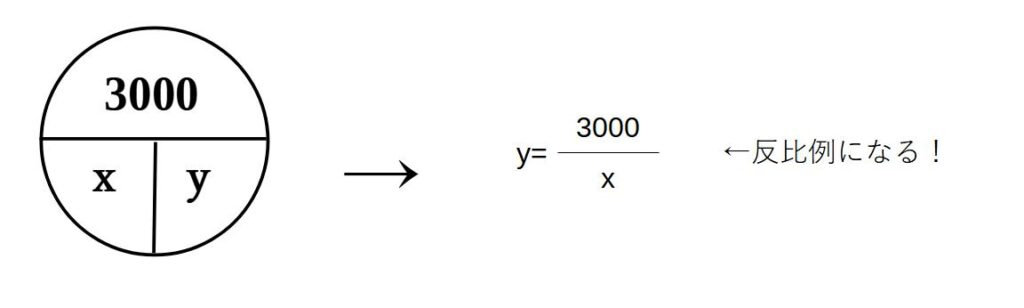
②毎分60mの速さ　→　ｘ＝60となるので、

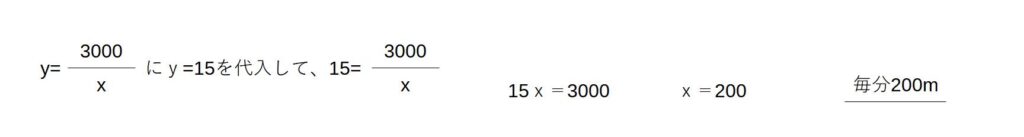
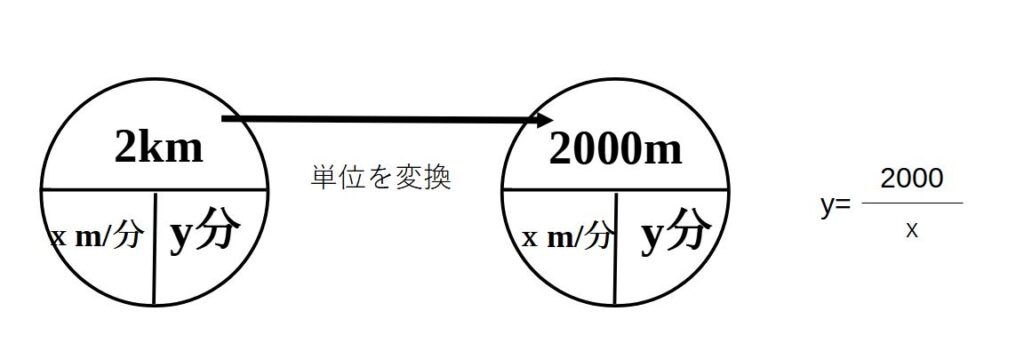
例4）家から学校までの2㎞の道のりを毎分xmの速さで歩いていくときにかかる時間をy分とする。このとき、ｙをｘの式で表せ

※こういった文章題の時、気を付けてほしいのは、「単位を合わせる」ということです。今回は２ｋｍと、毎分ｘｍという２つの違う単位が入っています。こういう時はあわてて計算をし始めてしまわないよう、いったん落ち着いて単位を合わせて、それから例の計算に入っていけるよう慣れておくようにしましょう。

例5）動点の問題

下図のような長方形ABCDで、点Pは辺BC上を毎秒3㎝でBからCまで動く。

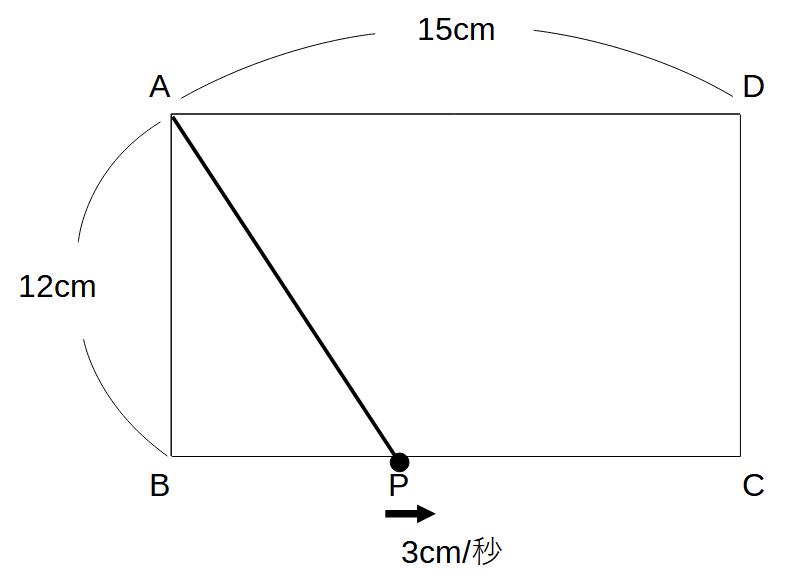
点PがBを出発してｘ秒後の△ABPの面積をｙ㎠とするとき、

①ｙをｘの式で表せ

②ｘの変域を求めよ

③ｘとｙの関係を表すグラフをかけ

④△ABPの面積が72㎠になるのは、点PがBを出発してから何秒後か

※動点の問題は定期テストや実力テストでもよく出ますので、解き方を覚えておきましょう。

解5）

①点Pは毎秒3㎝でBからCまで動く。点PがBを出発してからｘ秒後のＢＰの長さは

1秒後→3cm

2秒後→6㎝

3秒後→9㎝

→ｘ秒後は３ｘ㎝

よって、x秒後の△ABPの面積はｙ＝12×3ｘ÷２　　　

ｙ＝１８ｘ

②BC＝１５ｃｍ　→　点Ｐは5秒後にはＣに到着してしまう。よって

０≦ｘ≦５

③

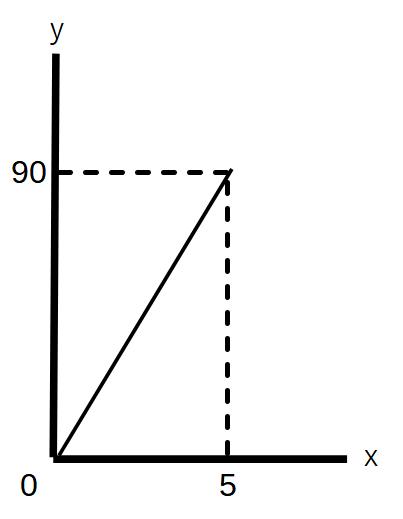
④△ABPの面積が72㎠　→　ｙ＝72

y=18ｘにy=72を代入

72＝１８ｘ

ｘ＝4　よって　4秒後

例6）歯車の問題

①歯数がｘで毎分6回転する歯車Ａに、歯数が12で毎分ｙ回転するはＢがかみ合っているとき、ｙをｘの式で表せ

※「歯車がかみ合っている」→回転したときに動いた歯数の量（総歯数）が等しい

歯車Ａ→歯車ｘで毎分6回転→1分間に動いた歯数はｘ×６＝６ｘ

歯車Ｂ→歯数12で毎分y回転→1分間に動いた歯数は12×ｙ＝12ｙ

よって、1分間で動いた歯数は等しいから、12y=6x　　∴ｙ＝1/2ｘ

②歯数が48ある歯車Aを20回転させると、歯数がｘの歯車Ｂがｙ回転する。

２つの歯車Ａ・Ｂがかみ合っているとき

ア．ｙをｘの式で表せ

イ．歯車Ｂの歯数が32のとき、歯車Ｂは何回転するか

ア．歯車→歯数48で20回転→この時動いた歯数は　48×20＝960

　　歯車Ｂ→歯数ｘでy回転→この時動いた歯数は　ｘ×ｙ＝ｘｙ

　かみ合っている→動いた歯数は等しくなるので

960＝ｘｙ　　　Y=960/x

イ．歯車Ｂの歯数が32→　ｘ＝32

y=960/x　に、ｘ＝32を代入

ｙ＝30　よって、30回転

中１数学へ→