今回は円について勉強します。
小学校でもやっていますが、他にもあったように新しい言葉や性質を覚えていかないと先へ進めません。覚えることが多いですが頑張りましょう。
(1)円の弧と弦
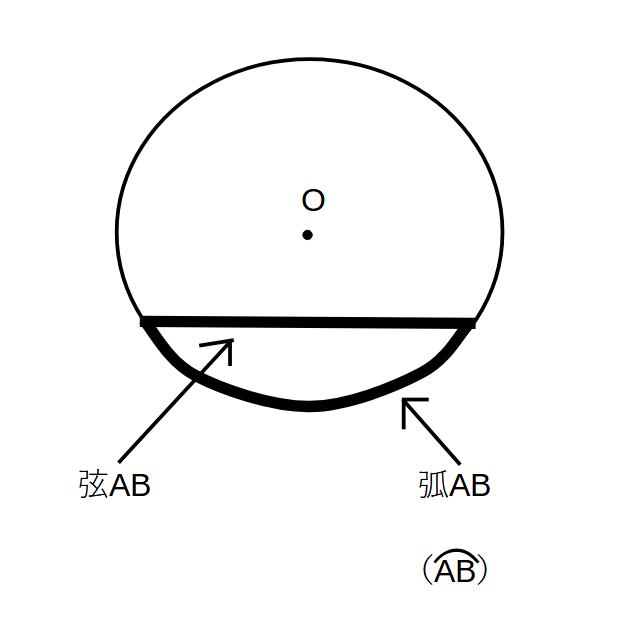
①点Oを中心とする円→円Oという
(円周は中心Oからの距離に等しい)
②円周の一部分を弧という
→2点A,Bを両端とする弧を弧ABといい、左図のような表記をする
③円周上の2点を結ぶ線分を弦という
→2点A,Bを両端とする弦を弦ABという
→長さが最も長い弦は直径、その時の弧は円の半周
※弧と弦を混同しないように注意すること!
(2)円の面積・円周とおうぎ形
小学校の復習にもなります。
円の面積=
(半径)×(半径)×(円周率=π)
小学校までは円周率を3.14で覚えました。それは変わらないのですが、中学校数学からは円周率を計算せず、π(パイ)とうい記号を使って表し、3.14をかける計算をしません!
円周の長さ=
(直径)×(円周率=π)
つまり、
例)半径3㎝の円の面積、演習の長さを求めよ。
面積 3×3×π=9π 9π㎠
円周 3×2×π=6π 6πcm
というように計算します。
おうぎ形
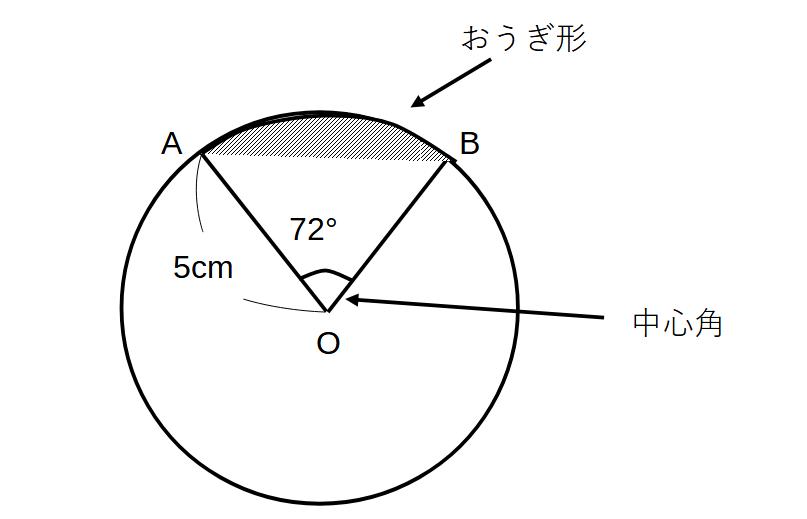
①円の2つの半径と弧で囲まれた図形をおうぎ形という
②おうぎ形で、2つの半径が中心で作る角(左図∠AOB)を中心角という
③おうぎ形の弧の長さと面積は中心角に比例する
おうぎ形の計算

※おうぎ形は、もともとの円全体に対してどのくらいの割合になるかを考える!
①中心角を使った考え方

②弧を使った考え方
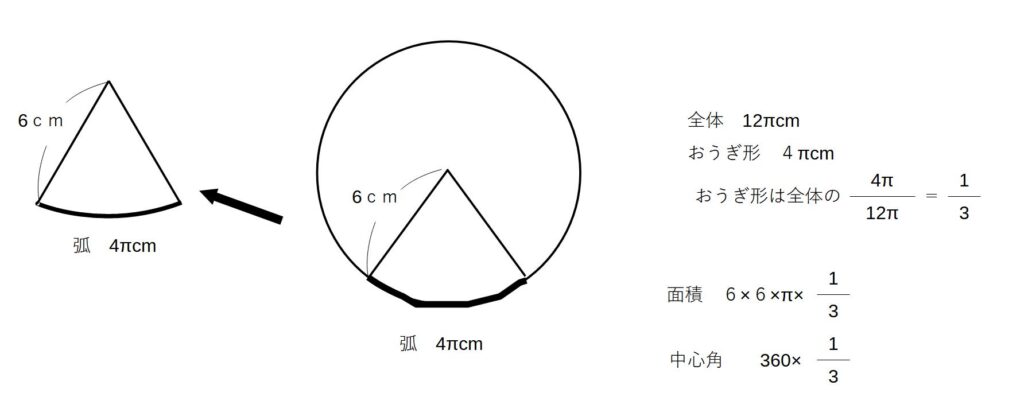
③面積を使った考え方
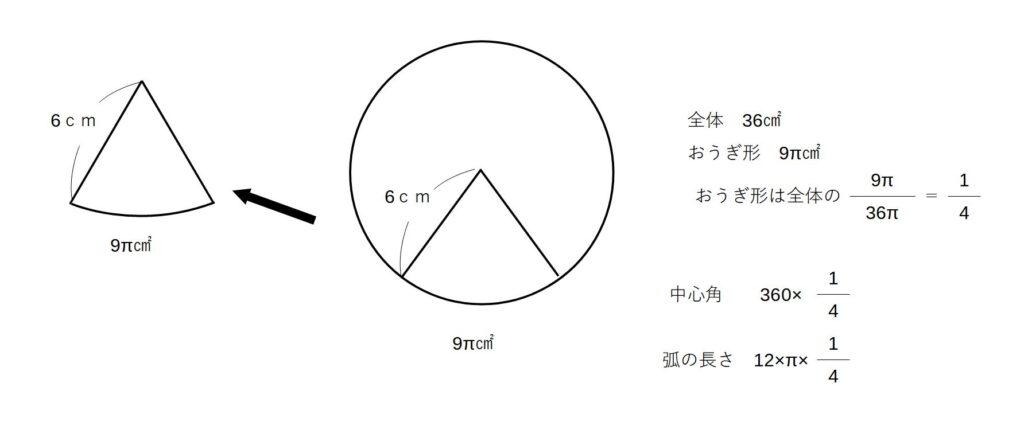
※おうぎ形の面積
1/2×(半径)×(弧の長さ)
が成り立つ
(3)円と直線
①円と直線の関係
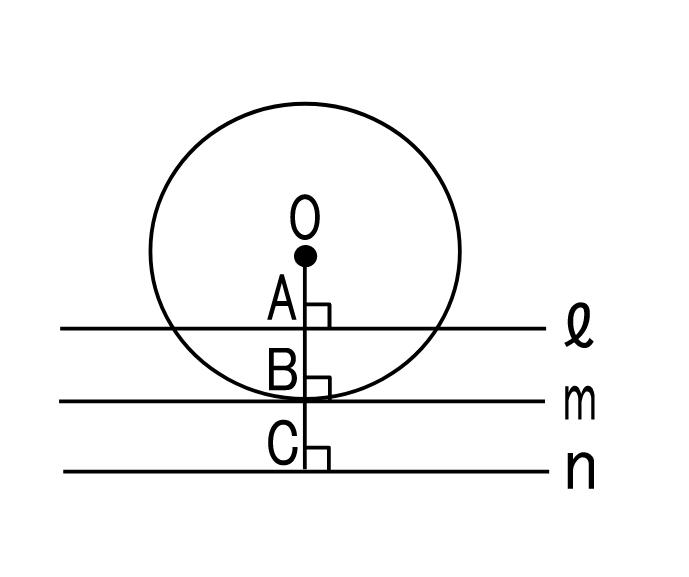
①直線ℓは円Oと2点で交わる
→中心Oとの距離(OA)は半径より短い
②直線mは接線
→線分OBの長さは半径に等しい
③直線nは円と交わらない
→中心Oとの距離(OC)は半径より長い
※接線とは、円と接する線のことを言います。
上記のことを言い換えると、次のようになります。
①中心Oと直線との距離が半径より短い
→その直線は円と2点で交わる
②中心Oと直線との距離が半径と同じ
→その直線は円と接する
③中心Oと直線との距離が半径より長い
→その直線は円とは交わらない(離れている)
②円の接線
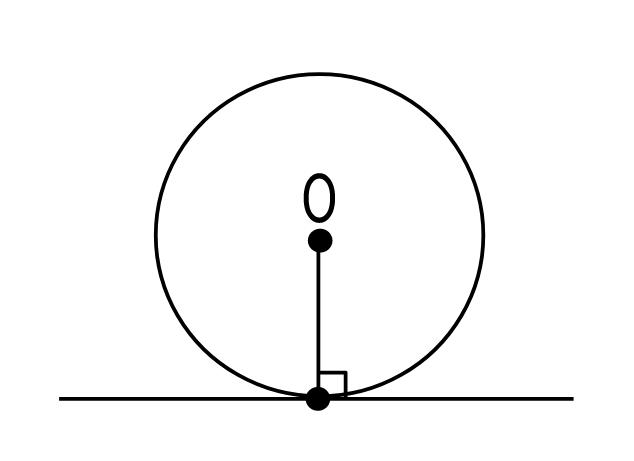
①円と直線とがある1点で交わるとき、「円と直線は接する」といい、この直線を接線、交わる点を接点という。
②円の接線は接点を通る半径と垂直になる。
③②より、円の中心Oと接線の距離は半径に等しい。
今回は円と直線について勉強しました。
新しい言葉の意味をしっかり覚えましょう。