(1)直線状の点を通る垂線
例)直線ℓ上の点Pを通る垂線を作図せよ。
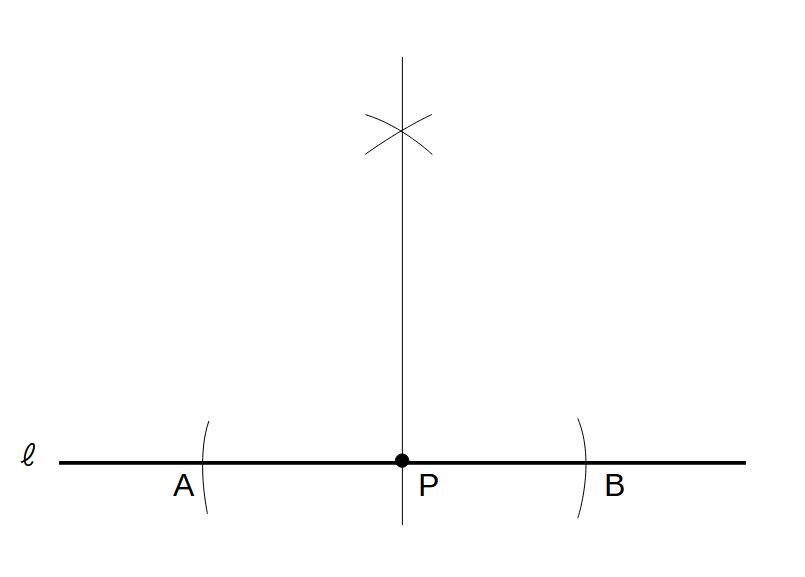
(手順)
①点Pを中心に円を書く
②①の円と直線ℓとの交点A,Bを線分として、垂直二等分線をひけばよい
→このとき円の交点は1つでOK
→点Pと交点とを結ぶ
ちなみに、垂線を立てる→直線ℓ=APB=180°なので、APBの垂直二等分線を引いていると考えることもできる
(2)直線上にない点を通る垂線
例)点Pを通り直線ℓに垂直な直線を作図せよ。
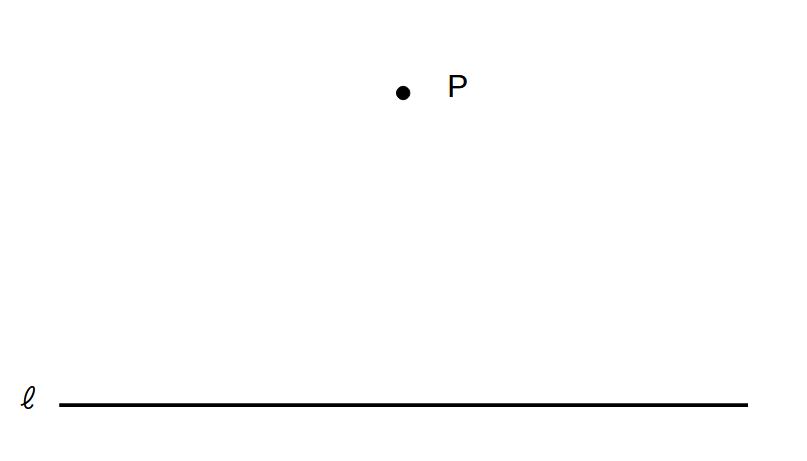

(手順)
①点Pを中心に直線ℓと交わる点をかく
②①の円を直線ℓとの交点A,Bを線分とする垂直二等分線をひけばよい
→このときも円の交点は1つでOK
③交点と点Pを結ぶ
例1)
図の△ABCのうち、辺BCを底辺としたときの高さを表す線を作図せよ。

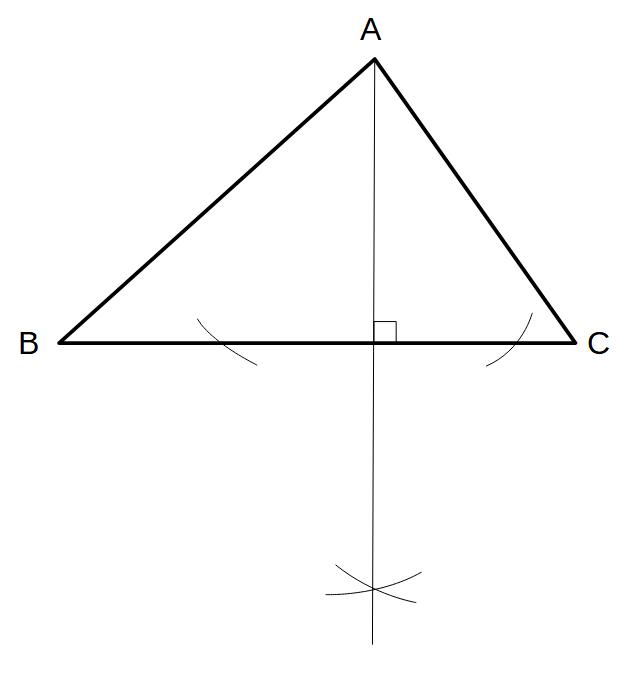
点Aを通り、BCに垂直な線をひけばよい
例2)最短距離=垂線
直線ℓ上に点Pをとるとき、PA+PBが最短になるように点Pを作図せよ
解1)
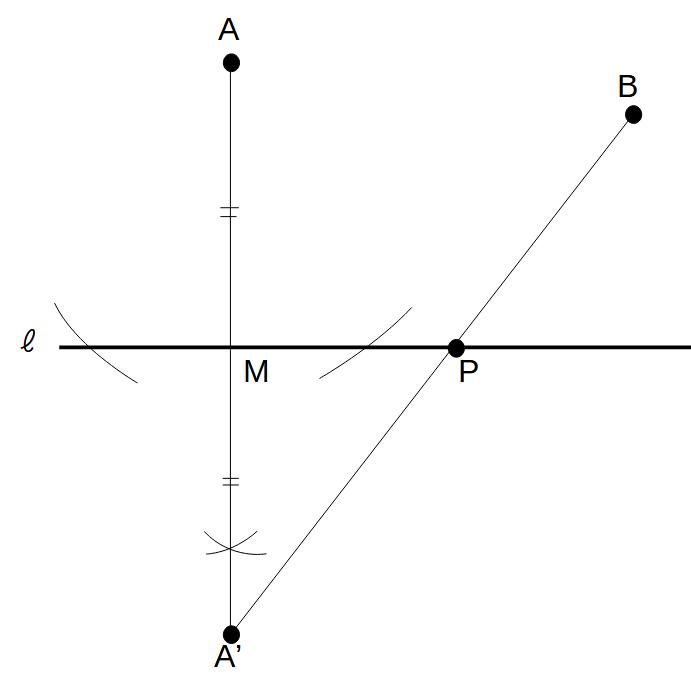
(手順)
①点を通り直線ℓに垂直な直線を引く(直線ℓとの交点をMとする)
②点Mを中心として、AM=MA’となるような点A’を①の垂線上にとる
③A’とBを結び直線ℓとの交点を求める→これが点Pとなる
(理由)①、②から、直線ℓが線分AA’の垂直二等分線になる
→直線ℓ上の点Pは必ずAP=A’Pとなる
→つまりAP+PB=A’P+PB
→A’P+PBが最短になるのはA’Bが直線のとき
よって、A’Bと直線ℓとの交点がPのとき、AP+PBが最短になる
(3)円の接線
例)点Oを中心として直線ℓと接する円を作図せよ
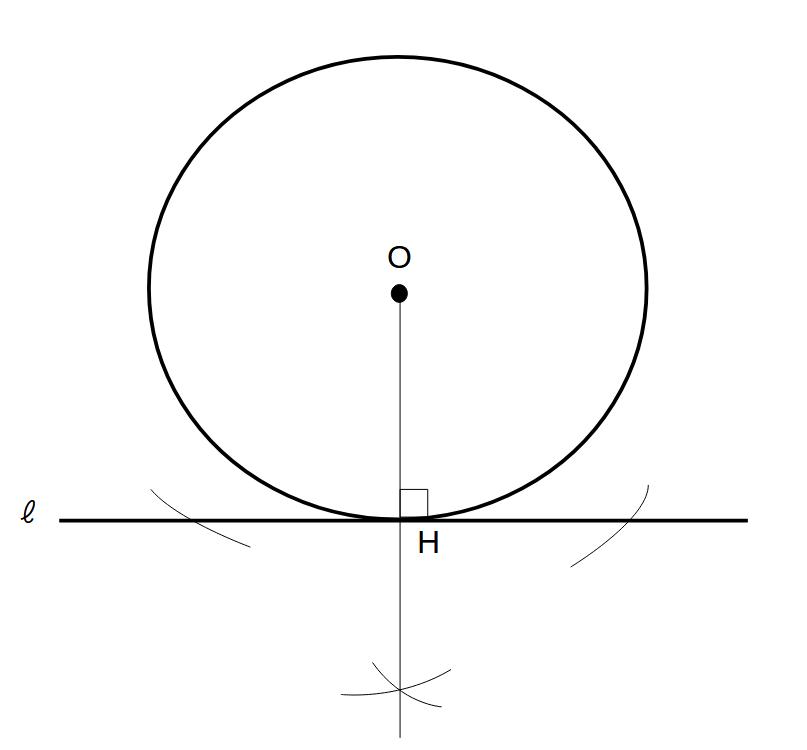
解)
(手順)
①点Oを通る直線ℓとの垂線を引く
②①の円と直線ℓの交点をHとするとき、OHを半径とする中心のOの円を書けばよい
※要するに半径を求める問題です。中心と直線との距離が半径と等しいとき、円と直線は接します。
→半径は中心と直線の距離となり、
点と直線の距離→垂線となります
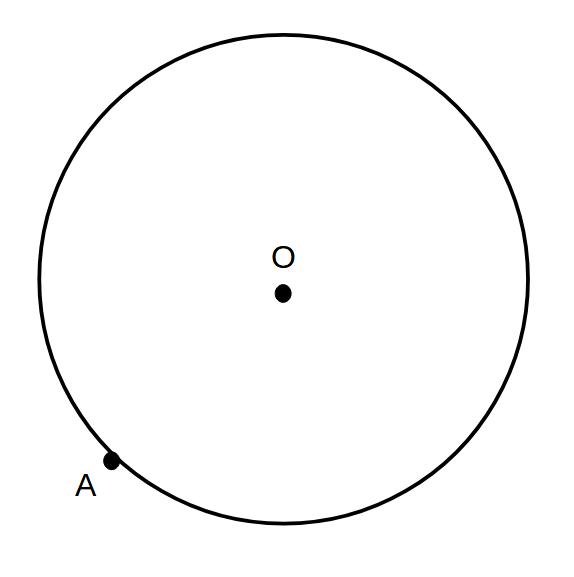
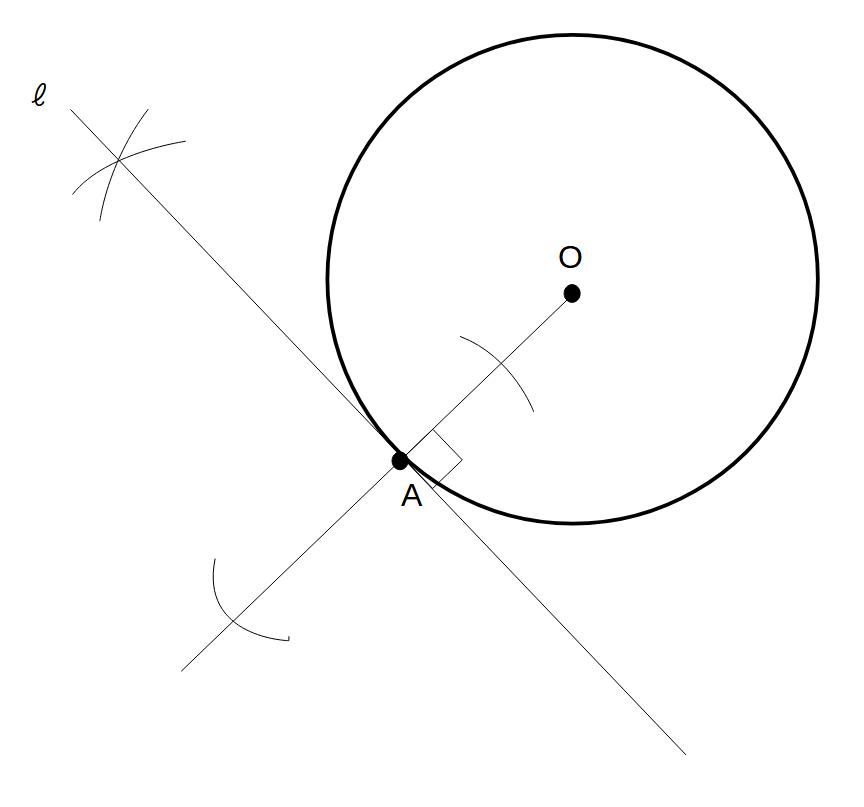
例)点Aで円と接する接線ℓを作図せよ
(手順)
点Aを通り、OAに垂直な直線を作図すればよい
※円の接線は接点と円の中心とを結ぶ半径と垂直に交わる
→垂直二等分線の作図を利用する!
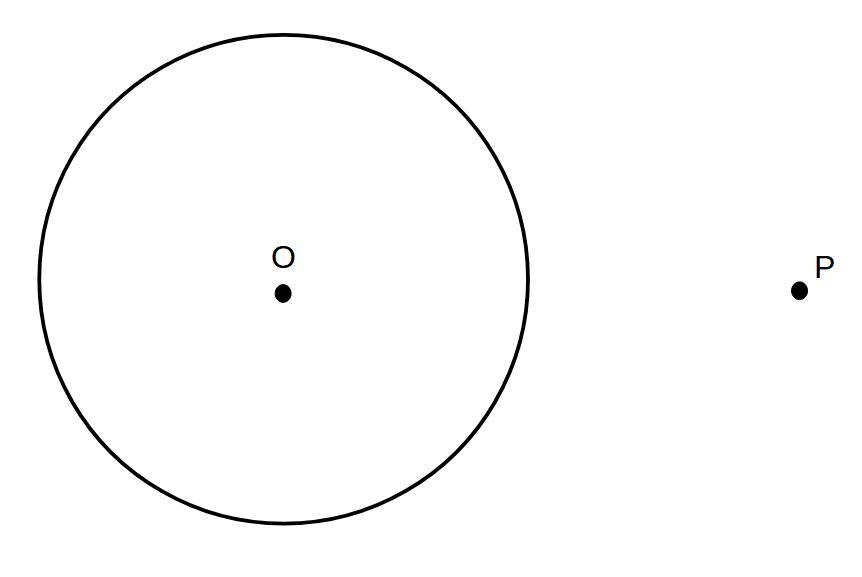
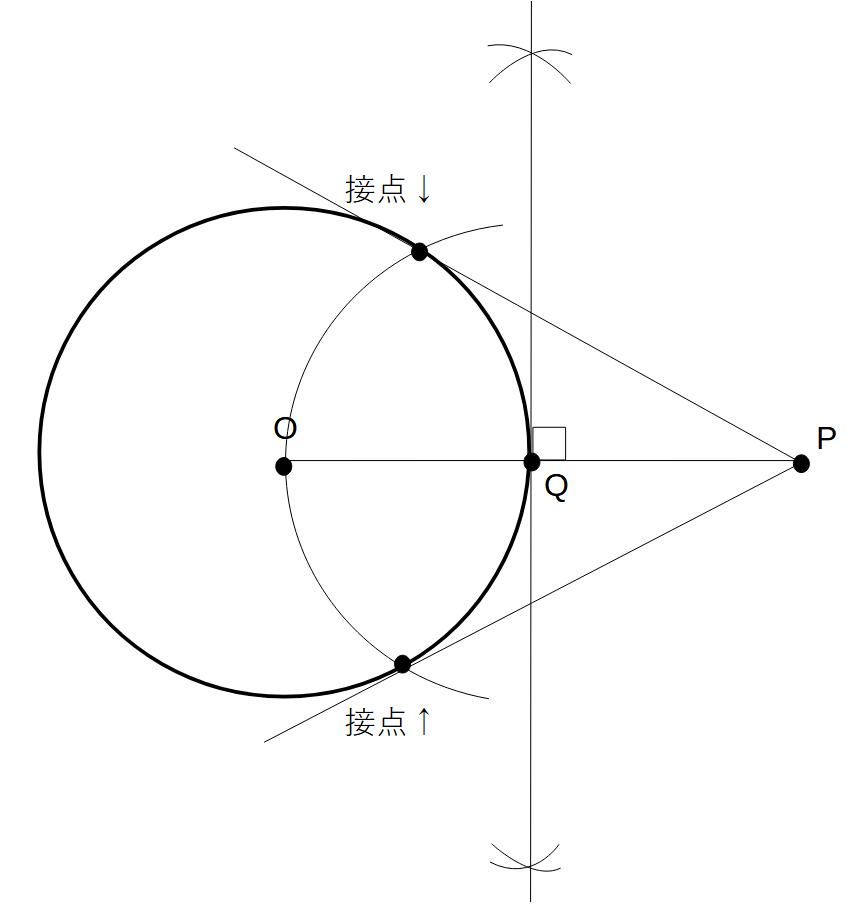
例)点Pから最短距離を通る円Oとの接線を2本作図せよ
(手順)
①OPを結ぶ
②OPの垂直二等分線を引く
③OPと垂直二等分線との交点をQとする
④Qを中心とした半径OQの円を書く
⑤2つの交点が接点となる
⑥Pから接点に2本直線を引く