(1)素因数分解
素数…1とその数自身の2つでしか割れない数。
(例)2,3,5,7,11,13,17,19…
※1は素数ではない!
素因数分解…数を素数の積で表すこと。
(例)6=2×3
60=22×3×5

(約数と素因数分解)
30の約数を求めよ。
30=2×3×5 …2,3,5を使ってできる数は?
2、 2×3 2×3×5
3、 2×5
5 3×5
答え1、2、3、5,6,10,15,30
(約数の個数の求め方)
A=ah×bh
Aの約数の個数=(n+1)×(m+1)
(例)
24の約数の個数
24=23×31
約数の個数
=(3+1)×(1+1)
=4×2
=8
∴8個
(2)2乗と素因数分解
144は何の2乗か
144=24×32 ←素因数分解するだけならここまででOK
=22×3×22×3
=122
※24×32をさらにばらすと、22×22×32となります。
このように、素因数分解して、すべての数字が2乗になるものは、必ず何かの数値の2乗という形に表すことができます。
☆2乗の数
⇒素因数分解をすると、
A×B×C × A×B×C のように
同じかたまりが2つできる!!
問 ①225
=3×5×3×5
=152
②256
=24×24
=162
③324
=2×32×2×32
=182
問 次の数にある数をかけて整数の2乗にしたい。
最も小さい数を求めよ。
①12
=3×22
A:3
※この問題は、ある数の2乗になる数は、素因数分解した場合、すべての数が2乗になるという性質を利用したものです。
①の場合は、2はすでに2乗になっているので、残った3が2乗になりさえすれば、何かの2乗になるはずなので、答えは3となります。
②60
=5×3×22
A:15
※この場合は、2乗になっていない数が2つ、5と3があります。
では、すべて2乗にするには、5と3をさらにかけてあげる必要があります。
なので3×5=15となります。
(3)公式の利用
例)次の式の計算をせよ。
①852-152
②982
③50×6.8-50×1.8
普通なら、この計算は面倒くさいですが、時間をかけて解くこともできます。
しかし、これらは今までやってきた乗法公式を使って計算すると、とても簡単に解くことができます。
早速見てみましょう。
①852-152
この式は、あの形に似ています。
A2-B2=(A+B)(A-B) ←これを使います
852-152=(85+15)(85―15) ←文字では分配法則を使いますが、すべて数値なので()を先に計算します
=100×70 ←簡単になりました
=7000
②982
この式も、見覚えのある式に変形できます。
=(100-2)2 ←この形は見覚えあるでしょう
(A-B)2=(A-2AB+B2)
(100-2)2=1002-2×100×2+22
=10000-400+4
=9604
③50×6.8-50×1.8
AB-AC=A(B-C)
50×6.8-50×1.8=50(6.8-1.8)
=50×5
=250
(4)式の値
①x=98のとき、x²+4x+4の値を求めよ。
x2+4x+4を簡単にしてから代入する!
=(x+2)2
=(98+2)2
=10000
②x+y=-5、xy=3のとき、x2+xy+y2の値を求めよ。
x2+xy+y2は
x2+2xy+y2に似ている→同じ形にしてしまう!
x2+xy+y2=(x+y)2-xy ←x2+xy+y2は、x2+2xy+y2からxyを引いた形になるので
=(-5)2-3
=22
※x+yを2乗して、後で帳尻合わせ!
※x2+y2=(x+y)2-2xy⇒これを【対称式】という。
問 ①x=5.7、y=4.3のときx2-y2の値
(x+y)(x-y)=(5.7+4.3)(5.7-4.3)=14
②x+y=-3、xy=1のとき、x2+3xy+y2の値
x2+2xy+y2+xy
=(x+y)2+xy=(-3)2+1=10
③x+y=-4、xy=2のとき、x2+y2の値
=(x+y)2-2xy=(-4)2-2×2=12
④x+y=-4、xy=3のとき、(x-y)2の値
(x-y)2
=x2-2xy+y2
=x2+2xy+y2-4xy
=(x+y)2-4xy=(-4)2-4×3=4
(5)式による説明
問)連続した2つの偶数の積に1を足した数は、その間の奇数の2乗になることを説明せよ。
今までもやりました、連続する数です。文字で表現する方法としていくつかありました。おさらいします。

解)連続した偶数…2n、2n+2
間の奇数 …2n+1 とおく。
2つの偶数の積に1を足すと、(⇒とりあえず式で表してみる)
2n×(2n+2)+1
=4n2+4n+1
間の奇数の2乗は
(2n+1)2
=4n2+4n+1
よって等しくなる。
問)連続する2つの整数の2乗の差は、その2数の和に等しいことを説明せよ。
連続する2数…n、n+1とおく。
2乗の差は、(n+1)2-n2
=n2+2n+1-n2
=2n+1
2数の和は、n+1+n
=2n+1
よって等しくなる。
問)半径rmの土地の周りに幅αmの道があり、道の中央を通る線の長さがℓmの道の面積S㎡とする。S=αℓとなることを証明せよ。
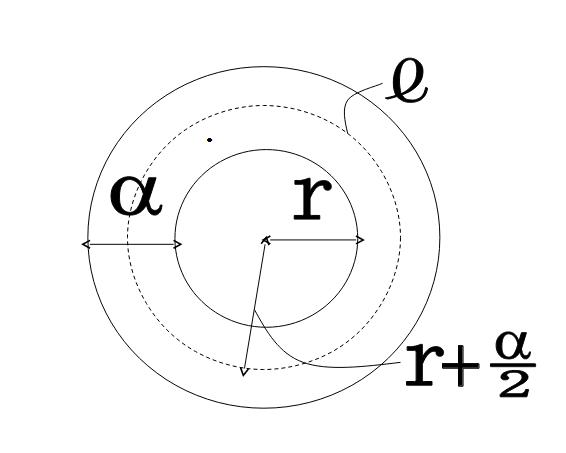
※ここで求められているものは何か→①円の面積Sと②円周ℓ
→S,ℓをそれぞれ計算する。
\( 解) 面積S= \pi (r+a)^2- \pi r^2=\pi (r^2+2ar+a^2)-\pi r^2=2\pi ar+\pi a^2 \)
\( \displaystyle 線ℓ= 2\pi (r+\frac{a}{2} )=2\pi r+\pi a=2\pi ar+\pi a^2 \)
\( よって、S=aℓ となる \)
問)1辺の長さaの正方形の土地のまわりに幅bの道があり、道の中央を通る線の長さℓ、道の面積Sのとき、S=bℓを説明せよ。
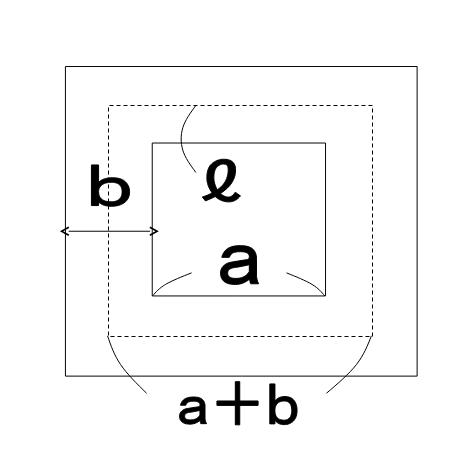
解)面積S=(a+2b) 2-a2
=a2+4ab+4b2-a2=4ab+4b²
線ℓ=4×(a+b)=4a+4b bℓ=b(4a+4b)=4ab+4b²
よって、S=bℓとなる。