今回は図形の合同と証明について勉強します。
証明問題などに触れていきますので、まずは決まり事をしっかりと覚えましょう。
(1)合同とは
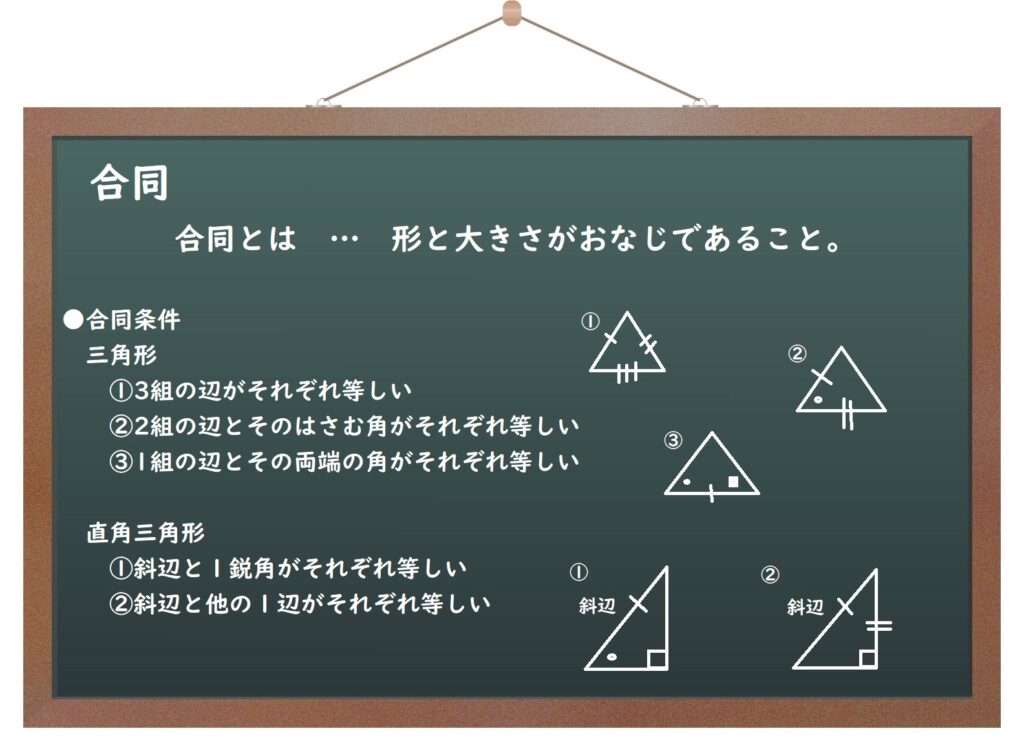
直角三角形が出てくる問題には、まず、直角三角形の合同条件をあてはめてみて、できなかった場合に普通の三角形の合同条件を考えていくようにしましょう。
では早速、合同条件を利用した証明問題を見ていきましょう。
問)
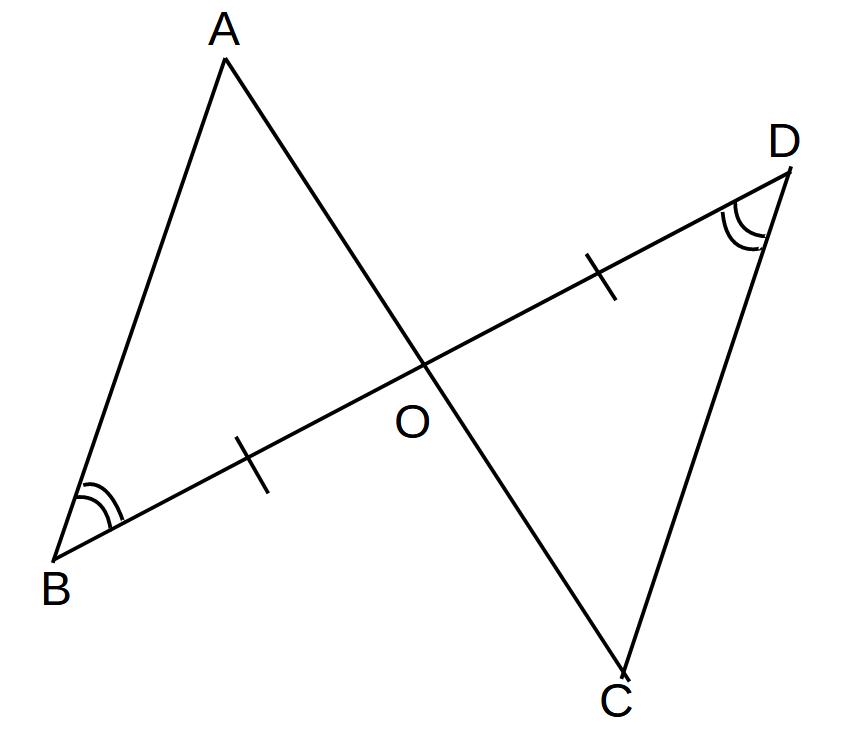
BO=DO、∠ABO=∠CDOのとき、AO=COを証明せよ。
※まず、AOとCOが対応するように、合同な三角形を見つけましょう。
解)
△AOBと△CODについて、仮定よりBO=DO…①
※「仮定より」とは、問題文にあることを指します。ここでは、問題文に書いてあるのでそのままCO=DOを書きました。
∠ABO=∠CDO…②
対頂角より∠AOB=∠COD…③
①②③より、1組の辺とその両端の角がそれぞれ等しいので、△AOB=△COD
※△AOBと△CODが合同であることが証明されました。合同ということは、すべての辺が等しいわけですから、
対応する辺より、AO=CO
さらにもう一ついってみましょう。
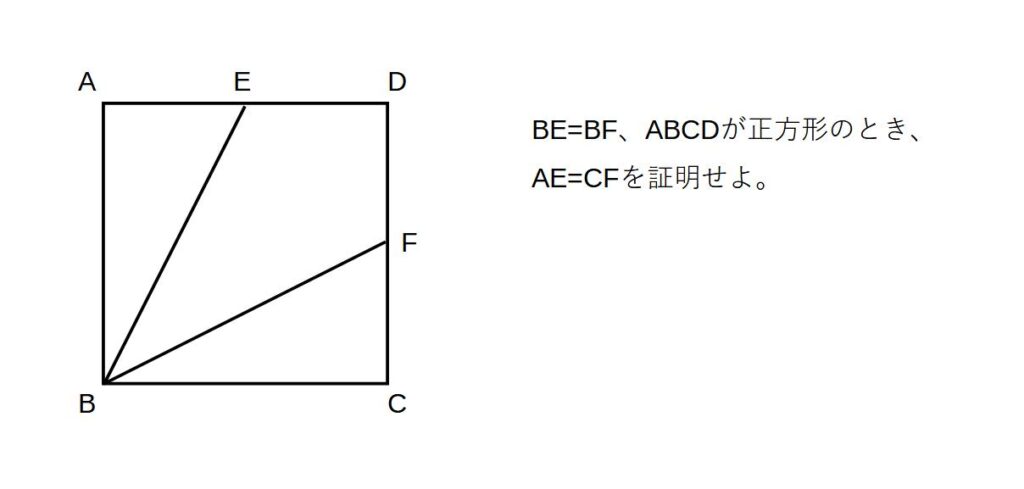
※直角が含まれているので、直角三角形となります。
ので、直角三角形の合同条件を使います。
解)
△ABEと△CBFにおいて、仮定よりBE=BF…①
※双方の三角形としてみて、問題文に斜辺が等しいことが書いてあるので、まずそれを①に
正方形の性質より、AB=CB…②
※問題文には、正方形であることが書かれているので、その性質(4辺が等しい、4角が等しい、90°であることも利用します。
∠EAB=∠FCB=90°…③
①②③より、斜辺と他の1辺がそれぞれ等しいので、△ABE≡△CBF
対応する辺より、AE=CF
※問題を解くときは、問題文に書いてあること(仮定)は必ず図形に書き込んでおく。
※図形の性質を使って条件を探していく。
※①②③と、必要な辺や角を書き出していく。書き方にはルールがあるので、そのルール通りに書く。
とにかく、図形の性質が頭に入っていないと、証明は全く歯が立たないことがお分かりいただけると思います。
まずは、図形の性質を覚えましょう。
(2)二等辺三角形
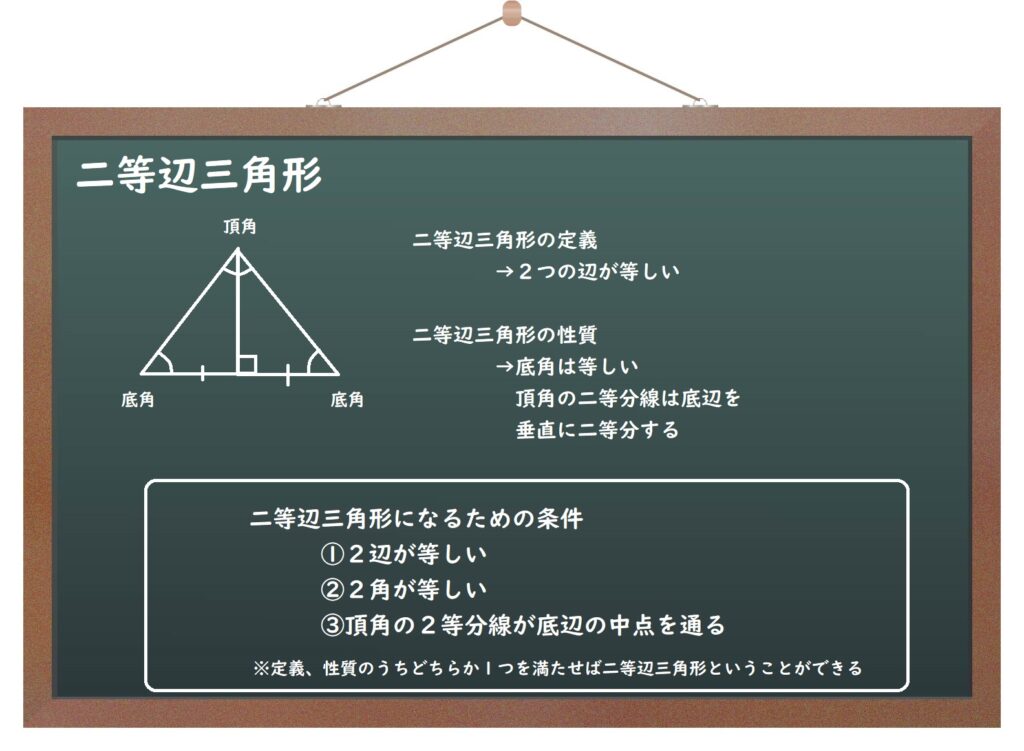
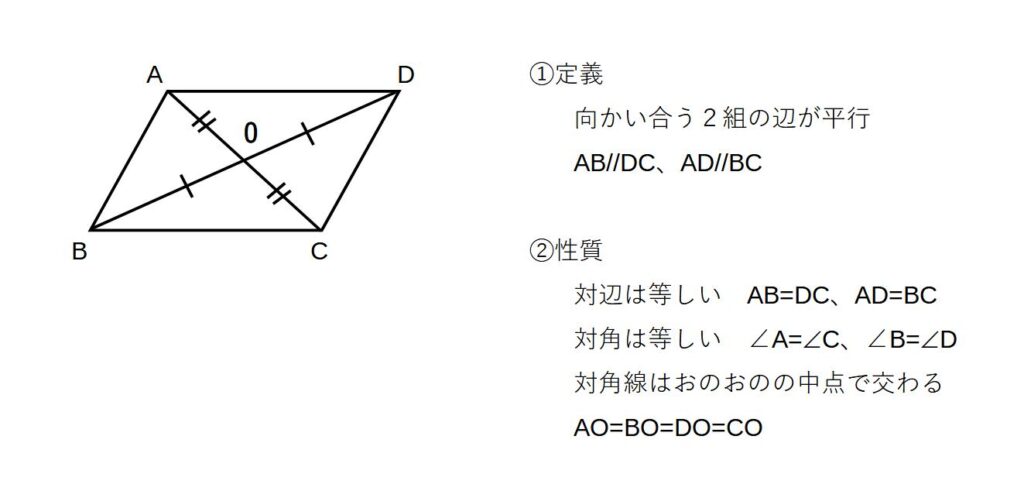
(3)平行四辺形
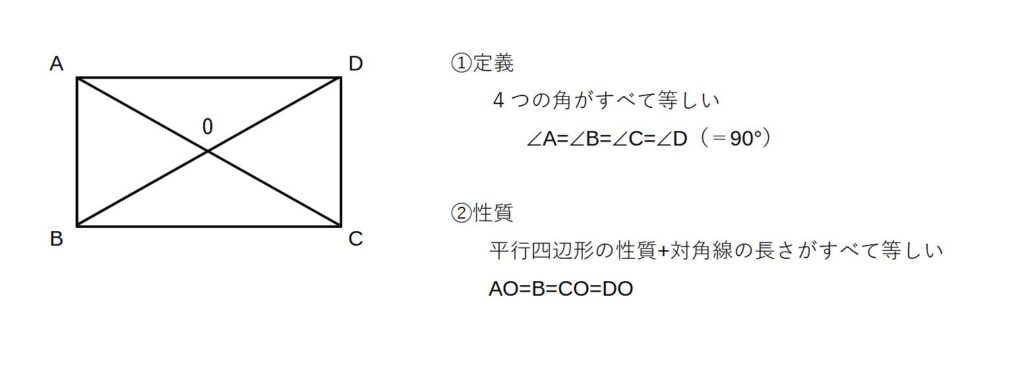
(4)長方形
長方形は、平行四辺形の一種と考えるとよい
(5)ひし形
ひし形も平行四辺形の一種と考えるとよい

(6)正方形

難しく書いてありますが、小学校でも聞いたことのあることを小難しく書いてあるだけなので、言葉に慣れてしまえばわかるようになると思います。
ここで、四角形に入ってやたら出てくる平行四辺形の条件をまとめておきます。
平行四辺形になる条件
※次のどれか1つを満たせば平行四辺形となる。
①2組の対辺がそれぞれ平行
②2組の対辺がそれぞれ等しい
③2組の角がそれぞれ等しい
④対角線がおのおのの中点で交わる
⑤1組の対辺が平行で長さが等しい
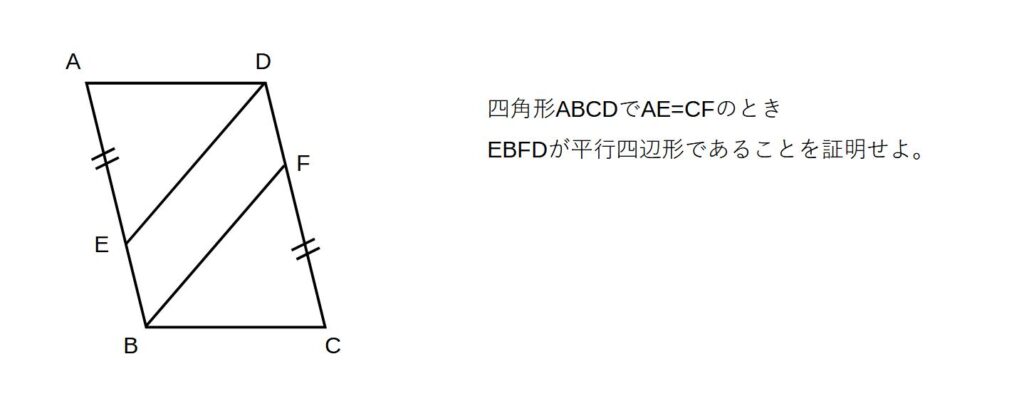
解)
平行四辺形の性質より
AB=CD…①
AB//CD…②
仮定より、AE=CF…③
①③より、BE=DF…④
②より、BE//DF…⑤
④⑤より、1組の対辺が平行で長さが等しいので、
EBFDを平行四辺形である
今回は合同と証明、特に図形の性質をおさらいしました。
図形の性質をしっかり押さえたうえで、たくさんの証明問題を解いてください。最初は答えを見て構いませんので、とにかく証明の形を身につけられるようにしましょう。