今回は比例・反比例の問題解法です。
早速行きましょう。
(1)式を求める

例1)yがxに比例し、x=2のときy=6である。
yをxの式で表せ。
※上記にあるように、「yがxに比例」なので、y=axに代入する
解1)y=axとおく
x=2,y=6を代入
6=2a
a=3 なので、 y=3x ←これが答え
例2)yがxに反比例し、x=4のときy=8である。
yをxの式で表せ。
※「yがxに比例し」とあるので、\( \displaystyle y=\frac{a}{x} \) とおく!
解2)
\( \displaystyle y=\frac{a}{x} \) とおく
\( x=2,y=8 \) を代入する
\( \displaystyle 8= \frac{a}{2} \)
\(a=16\) なので、 \( \displaystyle y= \frac{16}{x} \)
※別の解き方として
比例の場合 \( \displaystyle y=\frac{a}{x} \)
反比例の場合 \(a=xy\)
と表すこともできる
これはy=ax等を変形させただけの式ですが、計算をスムーズにするうえで便利ですので、余裕がある人は覚えておくとよいでしょう。
(2)表
yがxに比例するとき、次の表のKを求めよ。
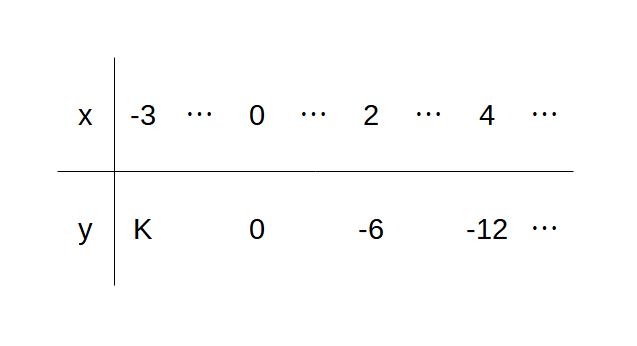
※x、yがわかっているところの数値を代入し、式を求める
解)x=2のときy=ー6
「比例」なのでy=ax
ー6=2a
a=ー3 なので y=ー3x
x=ー3のとき、y=9 K=9
(3)グラフ
例)次のl、mの式を求めよ。
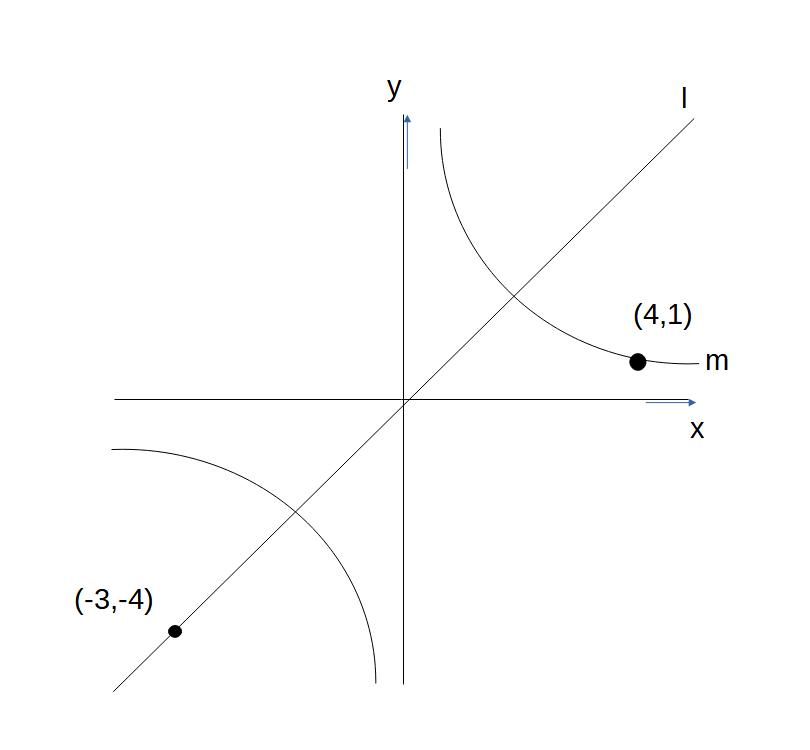
点の場所が多少変かもしれませんが、座標どおりにあるものとみてください。実際図形問題だと、わざとゆがんだ図形で出題されることもあります。
※これはlの直線が比例のグラフで、mの曲線が反比例のグラフであることがわかります。ですので、
左の直線上の座標(-3、-4)をそれぞれx=ー3,y=ー4として、比例の式に代入し、右の曲線上の座標(4,1)をそれぞれx=4,y=1として、反比例の式に代入して計算します。
解)
lは比例の式より、
\( y=ax \)とおける
(ー3,ー4)を通る直線なので、
\(-4=-3a\)
\( \displaystyle a=\frac{4}{3} \) \( \displaystyle y=\frac{4}{3}x \)
mは反比例の式より、
\( \displaystyle y=\frac{a}{x} \) とおける
(4,1)を通るので、
\( \displaystyle 1=\frac{a}{4} \)
\(a=4\) \(\displaystyle y=\frac{4}{x} \)
(4)応用
①歯車の問題
例)歯数が20である歯車Aを3回転させると、歯数がxである歯車Bがy回転する。yをxの式で表せ。
この問題は一見比例反比例とは関係なさそうに見えますが、ちょっとした応用で解答できます。
※歯車がかみ合っているとき、
歯数×回転数 → 一定
解)
\( 20 \times 3 = x \times y \)
(20の歯を3回転=xの歯をy回転)
\( xy=60 \)
\( \displaystyle y= \frac{60}{x} \) →反比例の式になる
②変域の問題
例)
\( \displaystyle y=\frac{a}{x} (a>0) \) において、\(2≦x≦16\) のとき、
\( 3≦y≦24\) である。aの値を求めよ。
この問題も実際にグラフを書いてみれば、xとyにそれぞれ対応する数値が見えてきます。
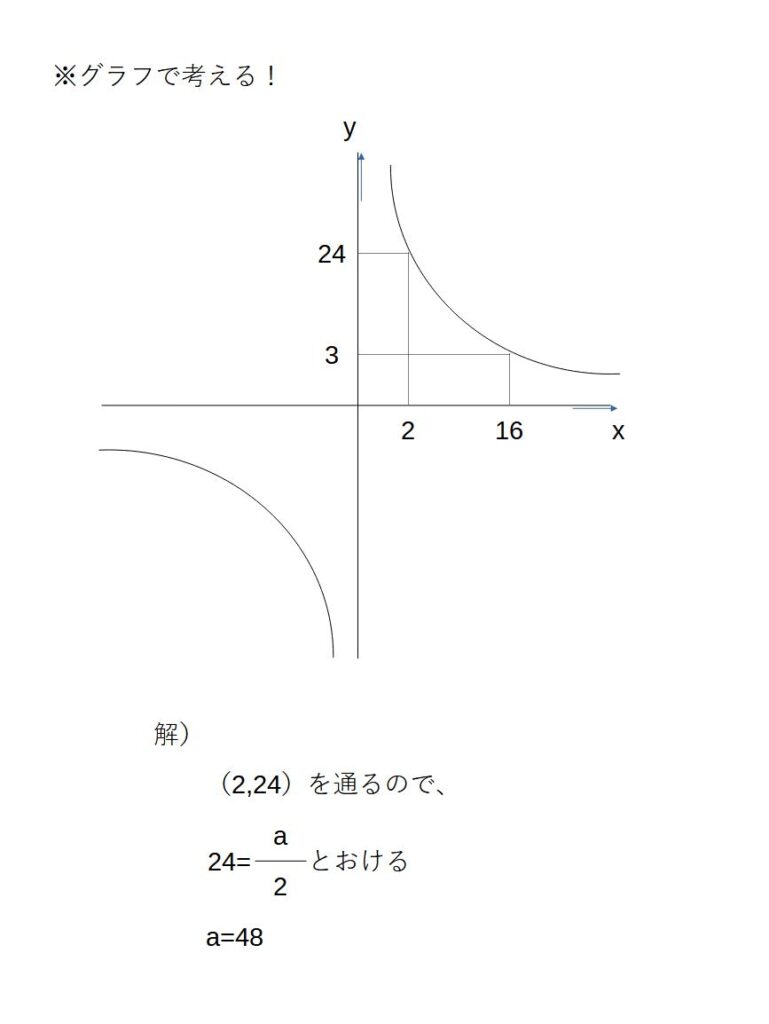
今回は比例反比例の問題解法について勉強しました。
基本的な部分やわからなかった部分については、それぞれの単元に戻りふりを行っていくようにしましょう。