(1)多面体
多面体とは…いくつかの平面だけで囲まれた立体
例)四面体、五面体など
※正多面体…すべての面が全く同じ正多面形で、どの頂点にも同じ数の面があつまっているへこみのない立体。
ちなみに5種類しかない。
(面の数)+(頂点の数)ー(辺の数)=2
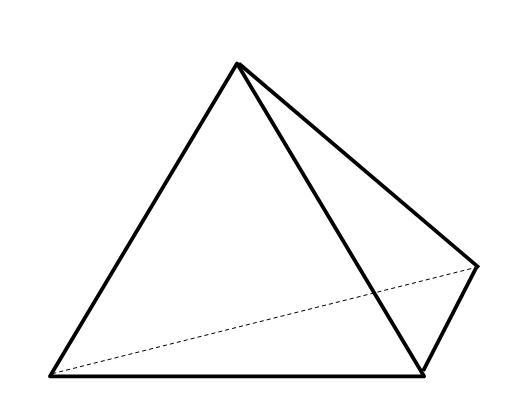
(正四面体)すべての面が正三角形
(2)角柱・円柱
角柱とは…平行に向かい合った1組の合同な多角形を底面とする柱状の立体。
側面は長方形である。
★正多角柱…底面が正多角形である角柱
側面の長方形はすべて合同
円柱とは…平行に向かい合った1組の合同な円を底面とする柱状の立体。
側面は局面であるが展開すると長方形になる。
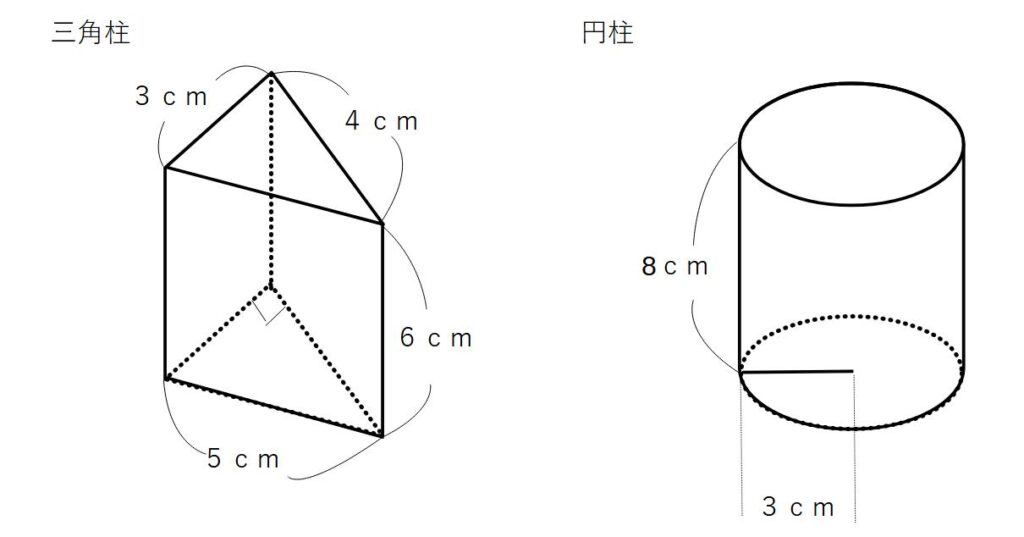
(見取り図)…切り開いて広げた図
角柱・円柱の体積
(柱体の体積)=(底面積)×(高さ)
※高さは2つの底面の距離になる。
(2つの底面は平行だから)
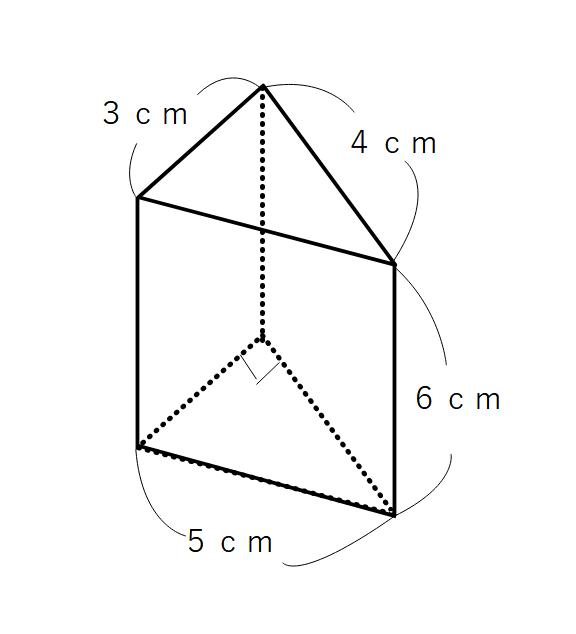
角柱の底面積
3×4÷2=6(㎠)
体積
高さは6cm
6×6=36㎤
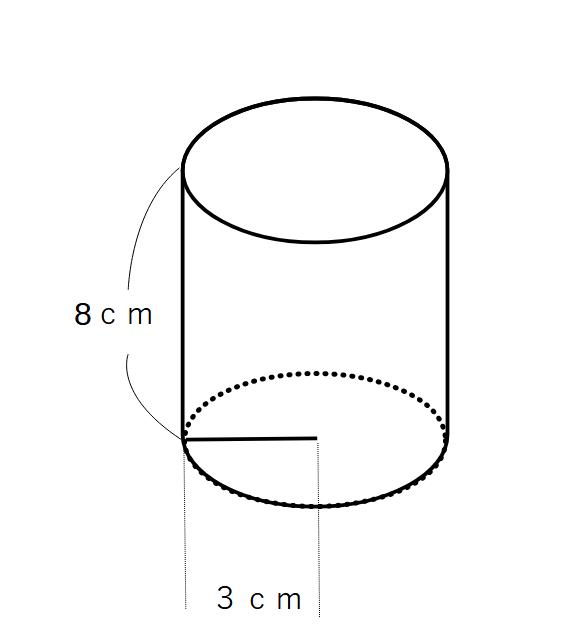
円柱の底面積
3×3×π=9π(㎠)
体積
高さは8cm
9π×8=72(㎤)
※底面の図形をきちんと押さえて面積を出しましょう
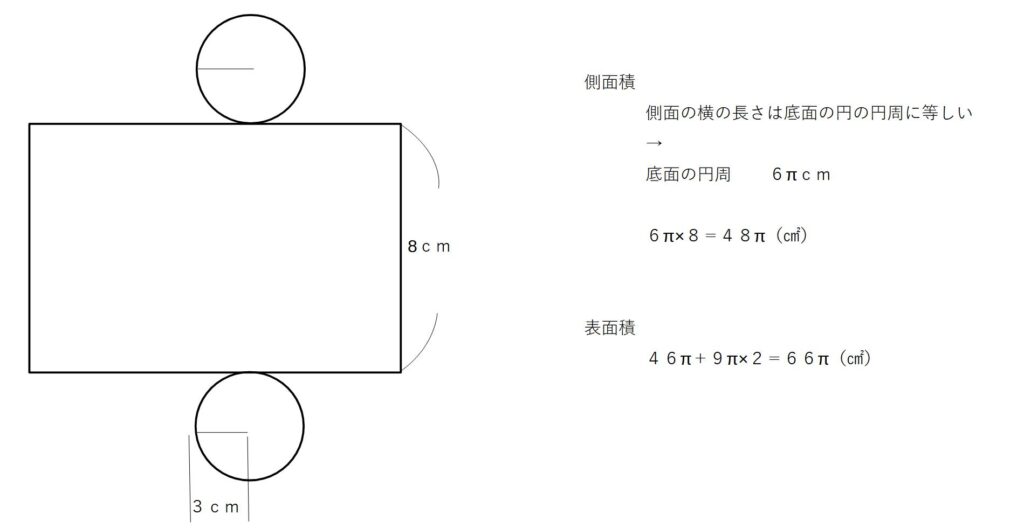
円柱・角柱の表面積
(柱体の表面積)=(側面積)+(底面積)×2
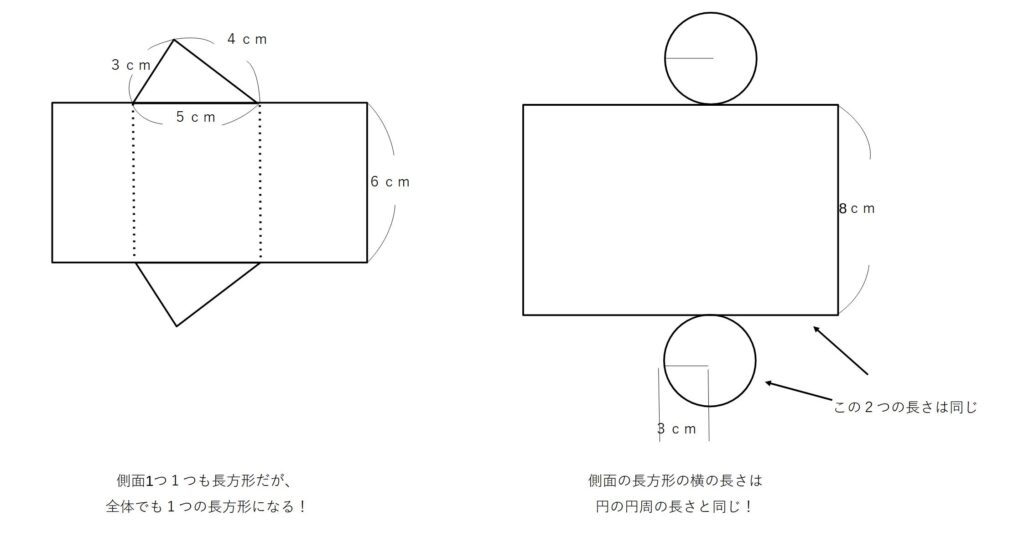
展開図を上手に使って側面積を出す
↓
角柱も円柱も側面全体で長方形を作っている
↓
(側面積)=(底面の周の長さ)×(高さ)

上の別解
側面全体を長方形として計算する方法
側面積=(3+4+5)×6
=12×6=72(㎠)
底面積=6(㎠)
表面積=72+6×2=84(㎠)
(3)円すい・角すい
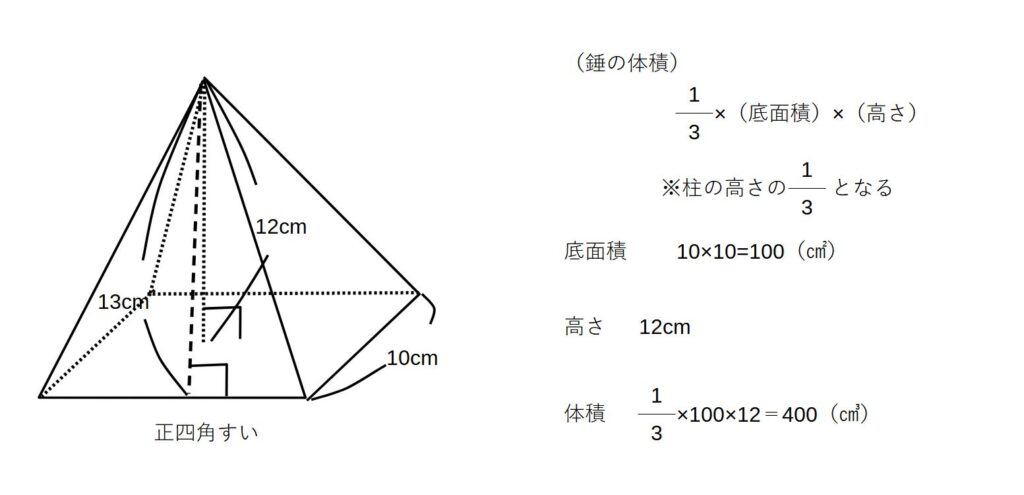
角すいの体積・表面積

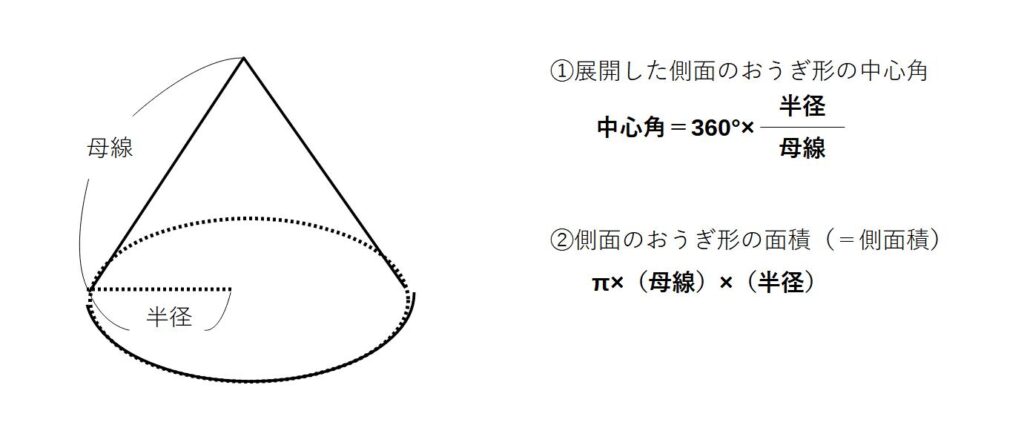
円すいの体積・表面積
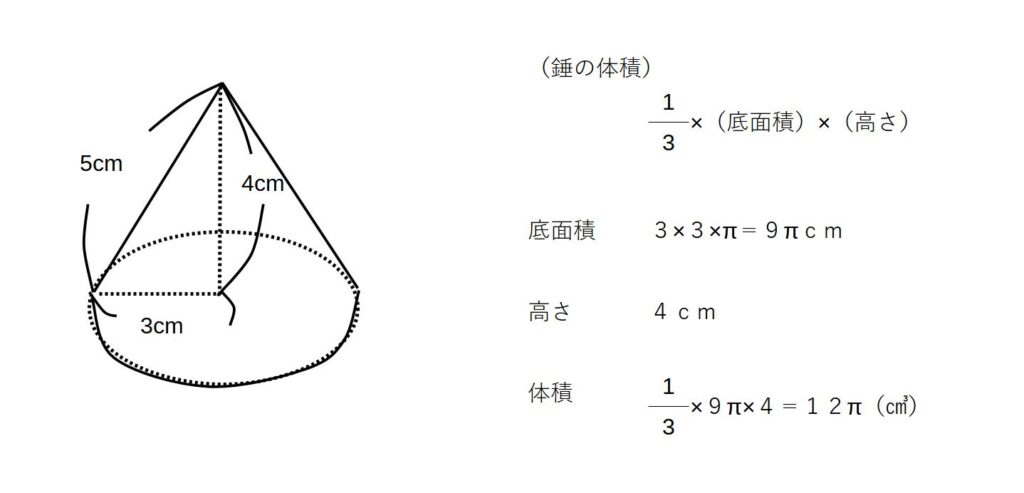
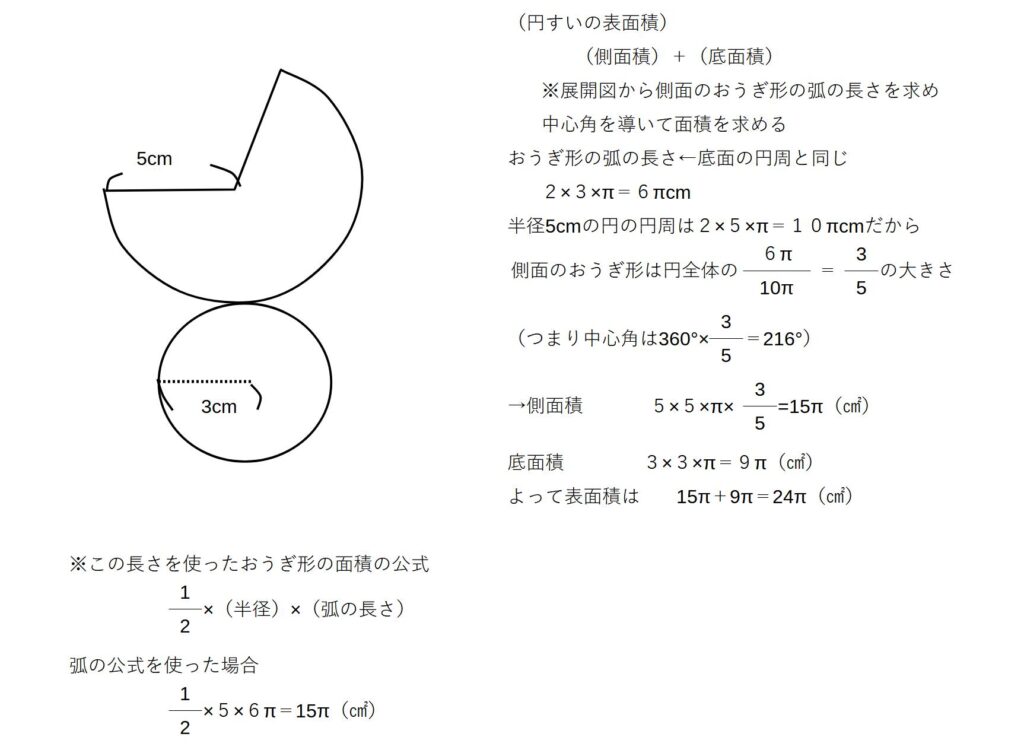
※円すいの側面のおうぎ形
(4)線や面を動かしてできる立体
円柱・角柱…底面の図形をそれと垂直な方向に一定の距離だけ動かしてできた立体
回転体…図形を1つの直線ℓの周りに回転させてできる立体 円柱・円すいなど
※直線ℓを回転の軸、回転体の側面を作る線分を母線という
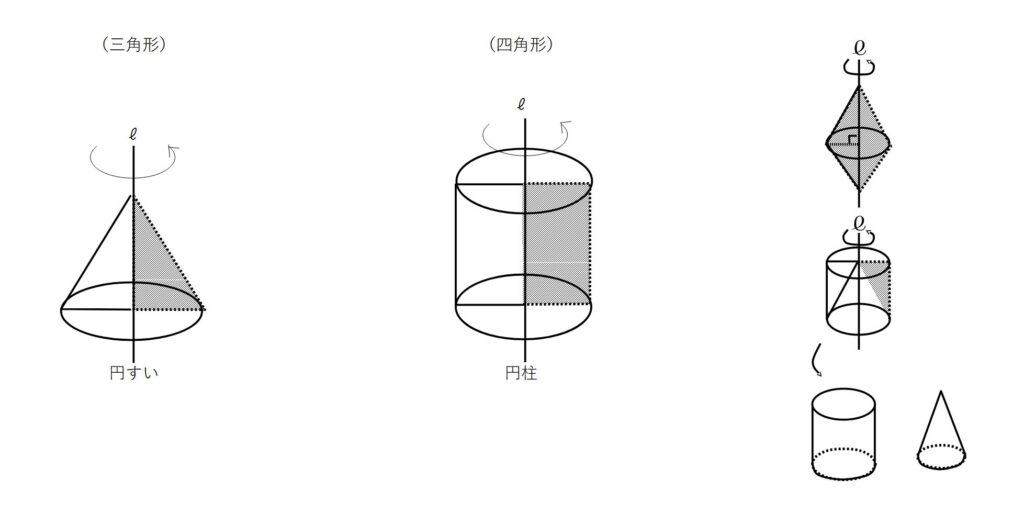
回転体の見取り図の書き方
①軸について線対称な図形を書く
②対応する点を面が円になるように結ぶ
軸に平行な面で切る→線対称な図形
軸に垂直な面で切る→軸を中心とする円