今回は連立方程式を勉強します。
1年で方程式を勉強しましたが、何がどう違うかをよく見ておきましょう。
x+2y=6 →xとyの2つが1つの式にある方程式(2元1次方程式という)の、xとyの値を求めたい。
①x+2y=6の場合
→=6になる場合のxとyを考えると…
②2x+3y=11の場合
=11になる場合のxとyを考えると…

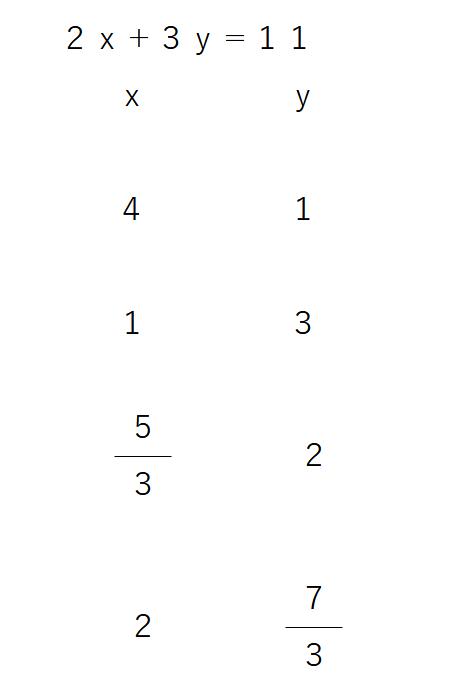
それぞれ何通りか候補が出てきます。
では、x+2y=6と2x+3y=11の両方の方程式を満たすxとyは?
→上の数値を見る限り、両方に共通している答えはx=4とy=1です。
では、このように、2つの式で共通するxとyを求めるためには、どうすればよいでしょうか?
\(\LARGE\begin{cases}x+2y=6 \\ 2x+3y=11 \end{cases}\)
それを新たな方程式で導き出すというわけです。この方程式を「連立方程式」といいます。
次回から、連立方程式の解き方を勉強していきます。