1次関数の式の求め方
(1)基本的な考え方
※求める1次関数の式を「y=ax+b」とおいて、与えられた条件をこれに当てはめていく
①傾きと通る1点が与えられている場合
例)傾き3,点(2,4)を通る直線の式を求めよ。
→傾きが3なので直線の式はまず
y=3x+bとなる。
点(2,4)を通るというので、これを代入する
4=6+b
b=ー2
よって、y=3x-2となる。
②2点(あるいはx、yが2種類)が与えられている場合
2点(4,4)(ー2,1)を通る直線の式を求めよ。
→求める直線をy=ax+bとおく
点(4,4)を通るので、まず、
4=4a+b…①
また点(ー2,1)を通るので、
1=ー2a+b…②
①と②を連立方程式として解く
すると、a=1/2、b=2となる。
よって、y=1/2x+2となる。
→②の別解
yの増加量…4-1=3
xの増加量…4-(ー2)=6
yの増加量/xの増加量なので、傾きは1/2、という方法もある
③切片を通る1点が与えられているとき
例)切片1,点(2,2)を通る直線の式を求めよ。
→切片1なので、直線の式をまず、
y=ax+1とおく
点(2,2)を通るので代入
2=2a+1
2a=1
a=1/2
よってy=1/2x+1
④グラフが与えられている場合
与えられたグラフから
①傾きを読み取る
②通る点を読み取る
③切片を読み取る
これらをy=ax+bにあてはめる
(2)いろいろな式の求め方
①平行な直線と通る点が与えられている
平行=傾きが同じ→①と同じになる
※平行=傾き同じ
垂直=傾きどうしをかけるとー1になる
②変域から直線の式を求める
→傾きが正の場合と負の場合とで、対応関係が異なるので、きちんと場合を分ける!
例①)y=aX+b(a>0)において、
ー2≦x≦4のとき、ー2≦y≦10である。
この1次関数を求めよ。
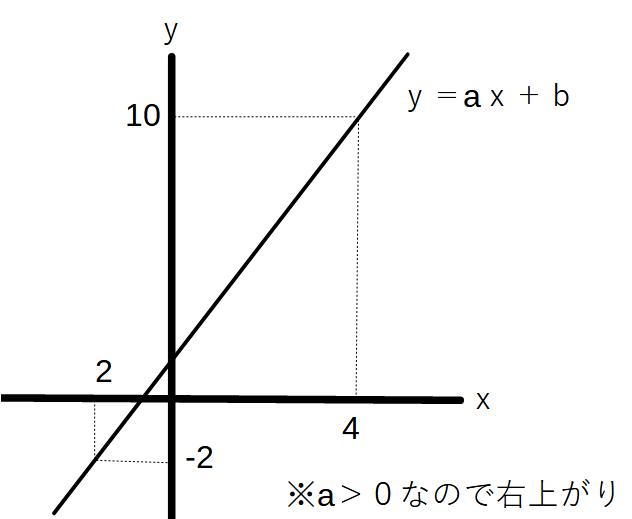
グラフと書いてみると、このようになる。
つまり、2点(2,2)(4,10)を通るということ
→それぞれをy=ax+bに代入した式を連立方程式にして計算すればよい
→よって、y=2x+2となる。
例②)y=ax+b(a<0)において、
ー2≦x≦2のとき、ー5≦y≦3である。
この直線の式を求めよ。
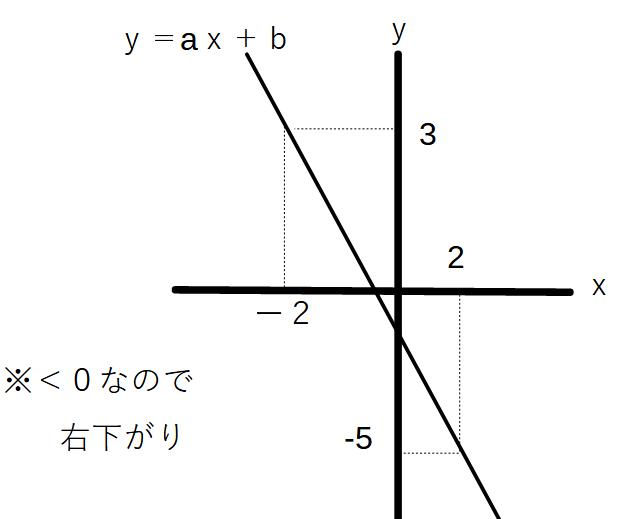
グラフに表すと、このようになる。
つまり2点(2,ー5)(ー2,3)を通るということ
→あとは同様に計算
y=ー2x-1となる。
※これらは、以下のように機械的に覚えてしまうのもOK
a>0のとき
〇≦x≦△、◇≦y≦☆
→(〇,◇)(△,☆)の2点を通る
a<0のとき
〇≦x≦△、◇≦y≦☆
→(〇,☆)(△,◇)の2点を通る
(3)ちょっと裏技
今までの方法で式を求められることはお分かりいただけたと思います。
ここからは、あとちょっとだけ速く、式が求まる技を伝授します。
その1
傾きと通る1点がわかれば切片を簡単に出せる技
例)傾きが3、点(1,4)を通る直線の式

と、このように計算できます。ちなみに答えはy=2x+1となります。
①かけて②符号を変え(チェンジ)③足すので、この技を「かけチェン足す」とか言ったり言わなかったり
その2
通る2点がわかっている場合の傾きの求め方
例)2点(1,4)(2,2)を通る直線の式
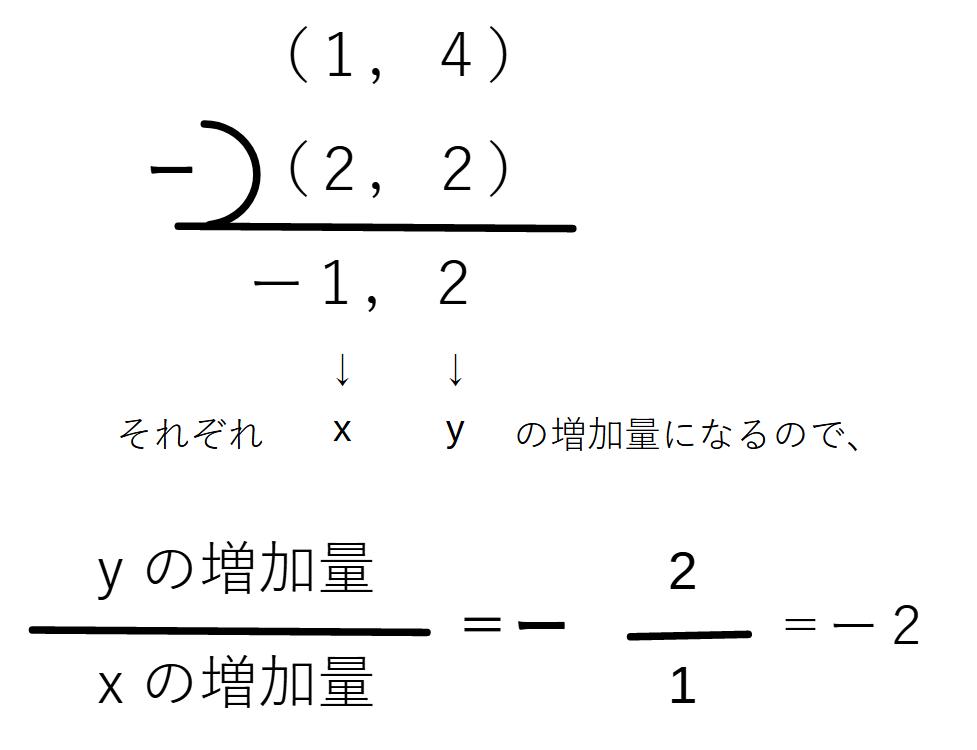
まず2点の座標を縦に引き算します。
そうすると、xとyの増加量がそれぞれ求まります。
それを計算して、傾きを求めます。
次は、切片ですが、傾きと点が1つわければOKなので、先ほどの手順で計算可です。

手順通り計算すれば、切片も求まります。
よって、y=ー2x+6
というように計算できます。
この技を使用すれば、たいていの1次関数の式は求まるようになります。
※ただし、このやり方は、(1,4)(3,4)を通る直線y=4、のようなx座標かy座標が同じ2点であるような直線(y軸、x軸に垂直、平行である直線の式)のケースではうまくいかないので注意しましょう。
傾きの範囲
傾きの範囲に関する問題の解法を勉強します。
例)y=axー2が線分AB(A(-8,-4)B(-2,-6))を通るようなaの値の範囲を求めよ。
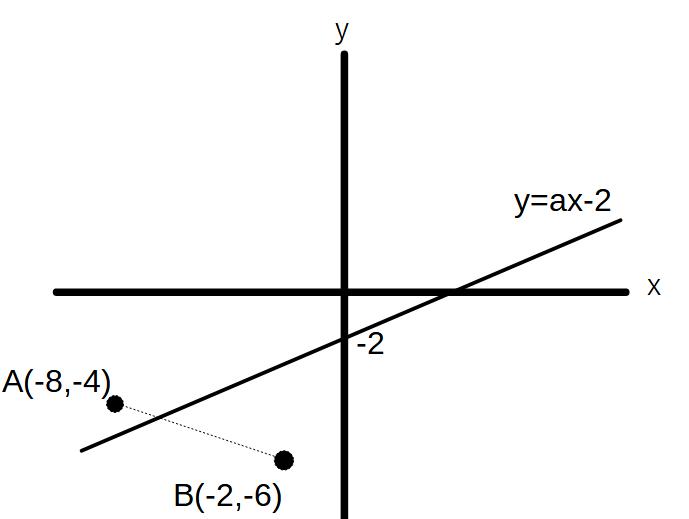
y=ax-2という式の通り、切片はわかっています。
切片は固定し、あとは傾きを求めることになります。
図のように、aの値が変化するにつれて直線の傾きが変化します。
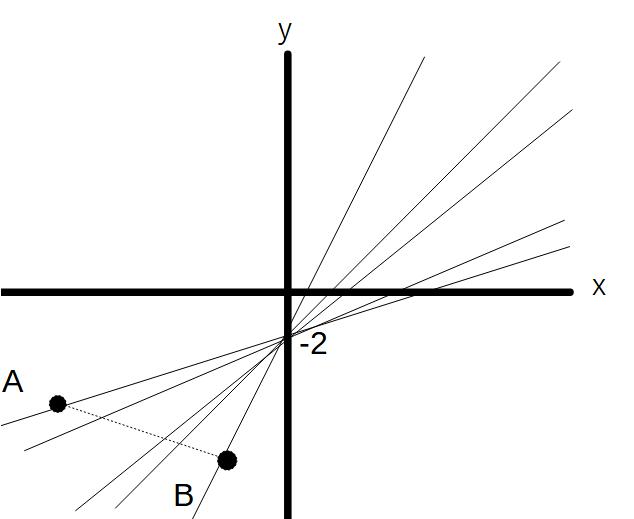
とすると、
傾きが最も大きくなるのは点Bを通るとき
傾きが最も小さくなるのは点Aを通るとき
→その間の傾きは、線分ABを通ることになります。
点B(ー2,ー6)を通るとき
ー6=ー2a-2
2a=4
a=2
点A(ー8,ー4)を通るとき
ー4=ー8a-2
8a=2
a=1/4
よって、1/4≦a≦2
類題として、傾きが固定されていて、切片の範囲を求める問題です。
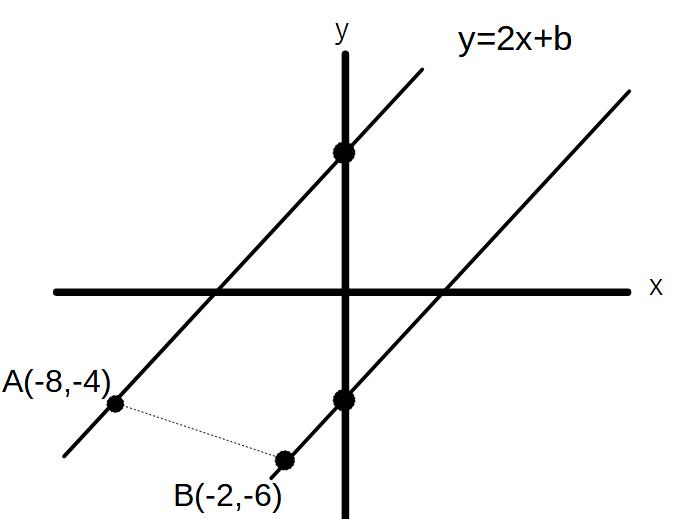
例)y=2x+bが線分AB(A(-8,-4)B(-2,-6))を通るようなbの値の範囲を求めよ。
→傾きが固定なので平行移動です。
①y=2x+bにAを代入 b=12
②y=2x+bにBを代入 b=ー2
よって、ー2≦b≦12