前回は正負の数(特に負の数)について、基本的な考え方を学びました。
では、今回はその正負の数を使った計算を勉強しましょう。
(1)正負の数の加法
※用語解説 足し算 → 加法(「かほう」とよみます)
足し算の答え → 和(「わ」とよみます)
正負の数の加法のやり方 (2パターンで考えます)
パターン1 同符号どうし
→ 絶対値の和に同符号をつける
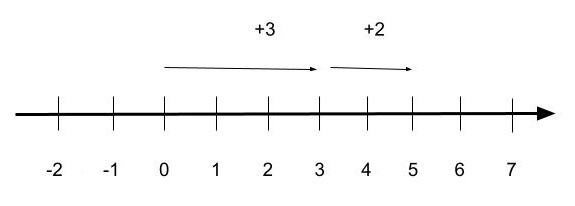
例①) (+3)+(+2)=+5
絶対値2と3を足して5、そして+をつける
数直線で考えると、下のようになります
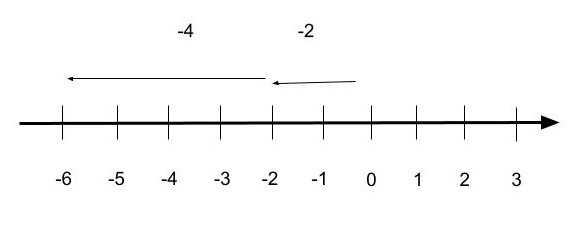
例②) (ー2)+(ー4)=ー6
絶対値2と4を足して6、そしてーをつける
数直線で考えると、下のようになります
パターン2 異符号どうし
→絶対値の大きいほうから小さいほうを引いて、
絶対値が大きい方の符号をつける
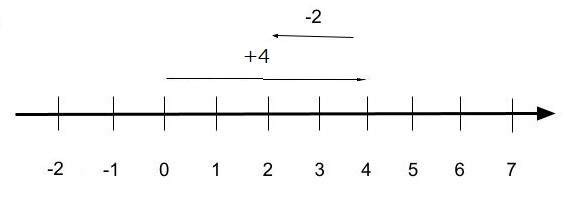
例①) (+4)+(ー2)=+2
絶対値の4から2を引いて、大きい方(4)についていたーをつける
数直線で考えると、下のようになります
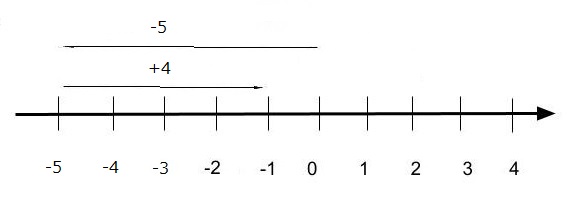
例②) (+4)+(ー5)=ー1
絶対値の4から2を引いて、大きい方(4)についていたーをつける
数直線で考えると、下のようになります
(2)正負の数の減法
※用語解説 引き算 = 減法(「げんぽう」とよみます)
引き算の答え = 差(「さ」とよみます)
正負の数の減法のやり方
例)(+5)ー(+2)
この式は、5から +2を「引く」という式になります。
これを
5から ー2を「足す」と考えます。
つまり
(+5)+(ー2) = +3
となります。

例①)(ー2)ー(+5)
=(ー2)+(ー5)
=ー7
例②)(+3)ー(ー2)
=(+3)+(+2)
=+5
(3)加減の混じった計算
①パターン1(かっこがついているパターン)
(+2)+(+3)ー(+9)ー(ー5)+(ー3)
●ステップ1→すべて加法にする
=(+2)+(+3)+(ー9)+(+5)+(ー3)
●ステップ2→正の数・負の数どうしにまとめる
=(+2)+(+3)+(+5)+(ー9)+(ー3)
●ステップ3→同符号どうしで計算する
=(+10)+(ー12)
●ステップ4→異符号どうしの計算をする
=ー2
②パターン2(かっこがついていないパターン)
4-8+5-12
●ステップ1→すべて足し算にする
=(+4)+(ー8)+(+5)+(ー12)
●ステップ2→正の数・負の数どうしにまとめる
=(+4)+(+5)+(ー8)+(ー12)
●ステップ3→同符号どうしで計算する
=(+9)+(ー20)
●ステップ4→異符号どうしの計算をする
=ー11
今回は、正負の数の加減算について勉強しました。最初のうちはステップを踏んでゆっくり問題を解いてみましょう。慣れてくればステップを飛ばして計算できるようにもなります。