(1)直角三角形の定義
①1つの角が直角である三角形を直角三角形という
②直角に対する辺を斜辺(しゃへん)という
※鋭角と鈍角
①90°(直角)より小さい角を鋭角
②90°(直角)より大きく、180°より小さい角を鈍角
③3つの角がすべて鋭角である三角形を鋭角三角形
④1つの角が鈍角である三角形を鈍角三角形
(ちなみに直角三角形の残りの2角は必ず鋭角)
(2)直角三角形の合同条件(定理)
①斜辺と1鋭角がそれぞれ等しい
②斜辺と他の1辺がそれぞれ等しい
このうちいずれかが成り立てばよい
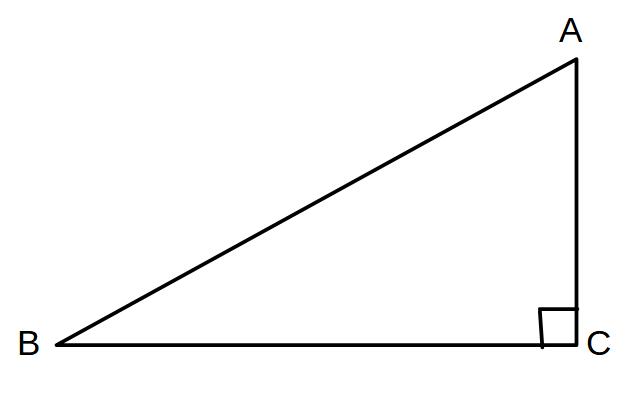
図でいうところの
辺ABが斜辺
∠BACと∠ABCは
必ず鋭角になる!
(3)角の二等分線
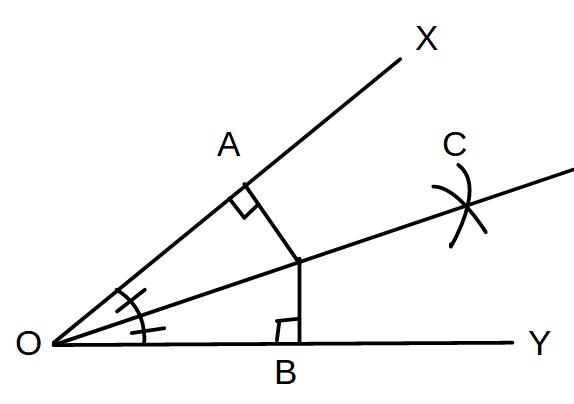
∠XOYの二等分線上に点Pをとり、PからOX、OYに引いた垂線とOX、OYの交点をそれぞれA、Bとする。
このときPA=PBであることを証明せよ。
△OPAと△OPBにおいて
∠PAO=∠PBO=90°(仮定)…①
∠AOP=∠BOP(仮定)…②
OP=OP(共通)…③
①、②、③より直角三角形の斜辺と1鋭角がそれぞれ等しいので
△OPA≡△OPB
対応る辺は等しいので
PA=PB
(4)円と接線
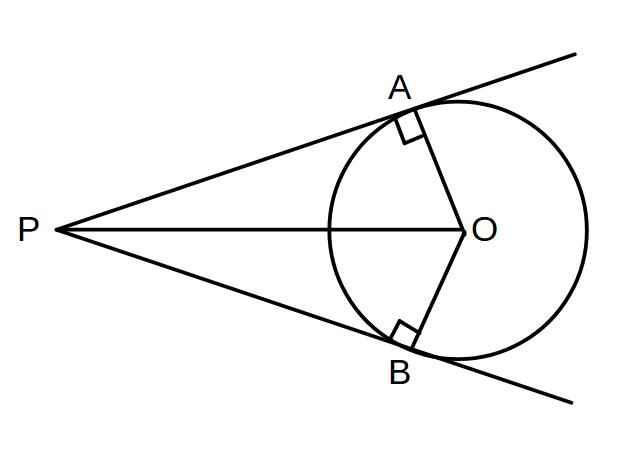
円外の点Pから円Oに2本の接線を引くと(接点A、B)
PA=PBであることを証明せよ。
(証明)
△OAPと△OBPにおいて
∠OAP=∠OBP=90°(円と接線との関係)
OP=OP(共通)
OA=OB(円の半径)
よって、直角三角形の斜辺と他の1辺がそれぞれ等しいので
△OAP≡△OBP
対応する辺は等しいので
PA=PB
次の章へ進む→