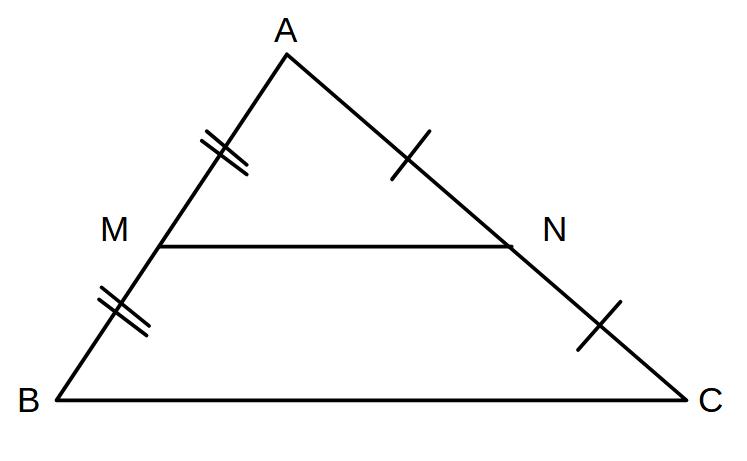
△ABCにおいて
AB、ACの中点をそれぞれM、Nとするとき
MN//BC
\( \displaystyle MN= \frac{1}{2} \)
三角形の2辺の中点を結ぶと、その線分は残りの1辺と平行で、かつ、その辺の長さの半分となる
例)
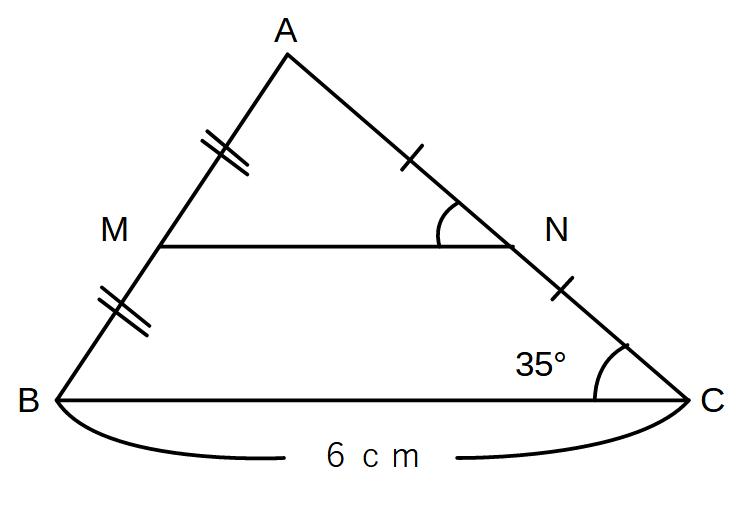
△ABCにおいてM、NがそれぞれAB、ACの中点となるとき
①∠ACB=35°のときの∠ANMの大きさ
②BC=6cmのときのMNの長さ
を求めよ。
例解)
中点連結定理より
MN//BC → 同位角(錯角も)等しい
\( \displaystyle MN= \frac{1}{2}BC \)
よって①MN//BCより同位角は等しいので
∠ANM=∠ACB=35°
②\( \displaystyle MN= \frac{1}{2}BC=3cm \)
※中点連結定理の逆
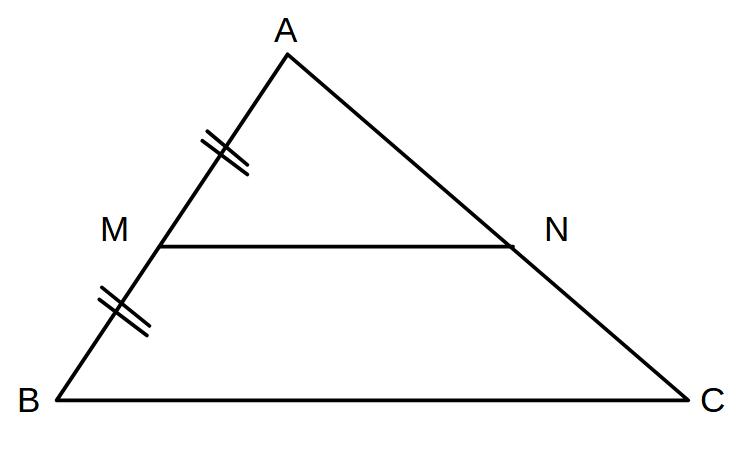
△ABCにおいて
MがABの中点(AM=AB)かつMN//BCならば
NもACの中点(AN=NC)となる
例1)
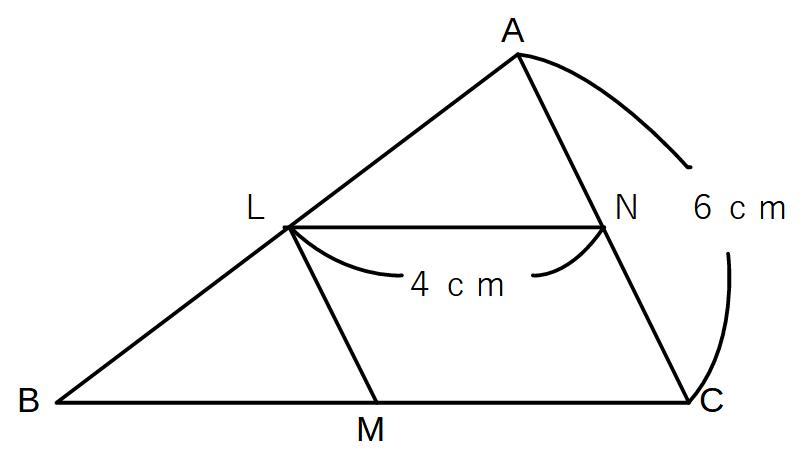
△ABCにおいて、L、M、NはそれぞれAB、BC、CAの中点であり
AC=6cm、LN=4cmである。
LM、BCの長さをそれぞれ求めよ。
例解)中点連結定理より、\( \displaystyle LN= \frac{1}{2}BC \)、\( \displaystyle LM= \frac{1}{2}AC \)
よって、LM=3cm、BC=8cm
例2)
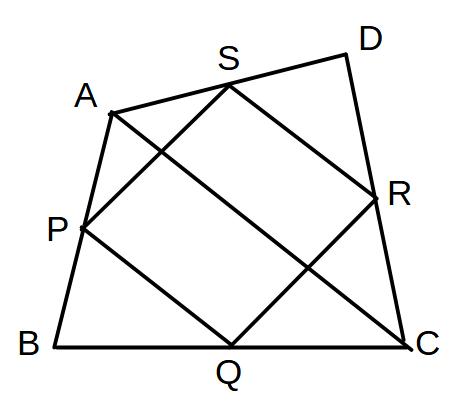
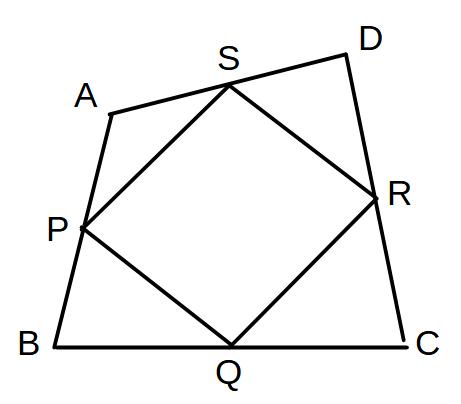
図の四角形ABCDにおいて
P、Q、R、Sはそれぞれ
AB、BC、CD、DAの中点であるとするとき
①四角形PQRSはどんな図形となるか
②①で答えた図形に四角形PQRSがなることを証明せよ
例解)
①四角形PQRSは平行四辺形である
②(証明)
まずAとCを結ぶ
この時△ABCにおいて中点連結定理により
PQ//AC…①
PQ=1/2AC…②
また△ACDにおいても同様に
SR//AC…③
SR=1/2AC…④
①、③より
PQ//SR…⑤
②、④より
PQ=SR…⑥
よって、⑤、⑥より四角形PQRSにおいて1組の対辺が平行で長さが等しいので
四角形PQRSは平行四辺形である