例1)
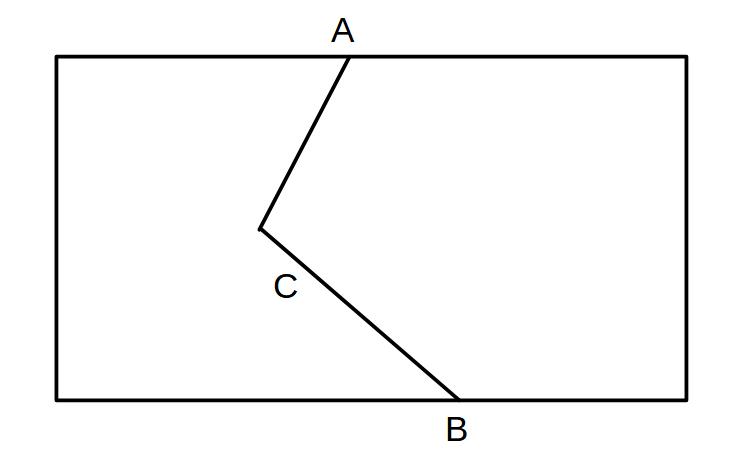
ある土地がA→B→Cという線で境界を分けられている。
2つの土地の面積を変えずにAから直線の境界線を引くにはどうするか。
①ABに直線を引く→△ABCに注目
→△ABCを面積を変えずに形を変えれば境界線を直線にできるはず(ほかの部分は変わらないから)
→2の平行線と面積の関係を利用!
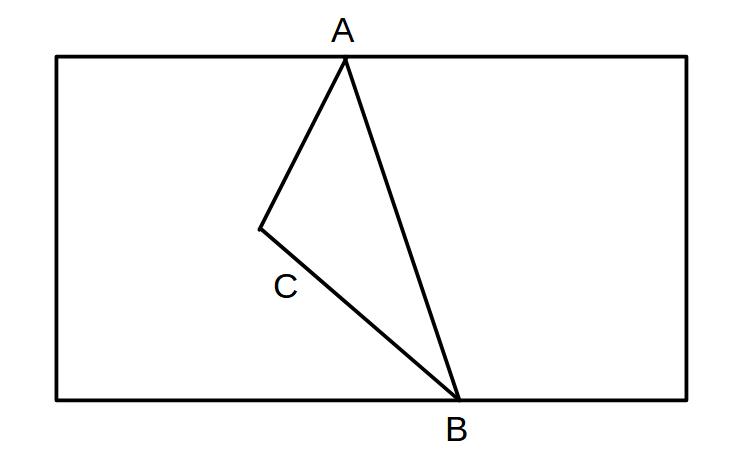
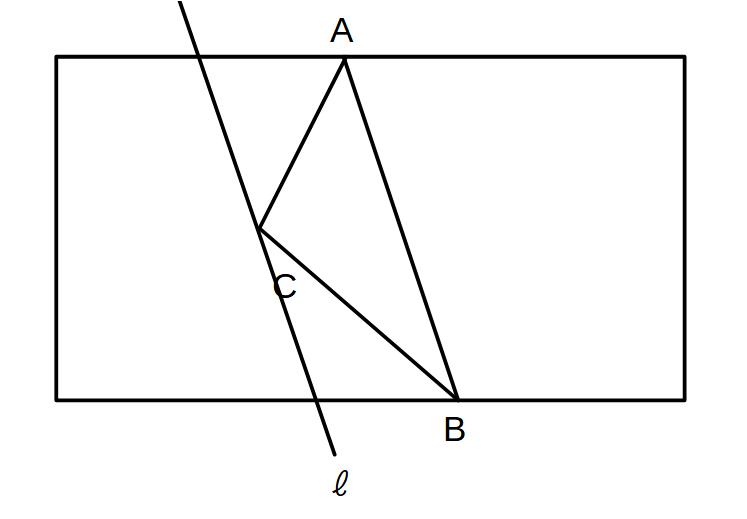
②点Cを通り、ABに平行な直線ℓを引く
→この直線上で点Cを動かせば△ABCの面積は変わらない
③点Aから直線ℓと長方形の下辺へ直線を引き、その交点をDとする。
→△ABCができる
→△ABC=△ABDなので、ADが条件を満たす境界線
(どちらも底辺ABが同じで、平行線上にあるので高さも一緒)
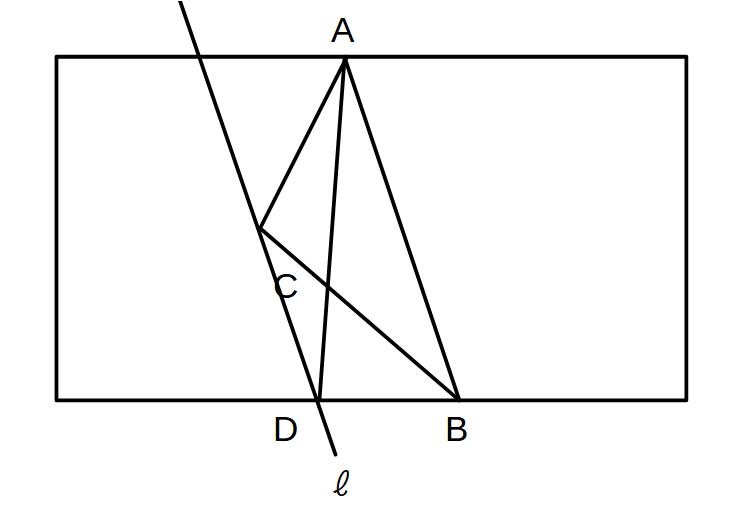
※ある三角形において、底辺を共通に(そのままに)底辺と向かい合う点を作り、底辺に平行な直線を引くと、その直線上の点ならどこでももとの三角形と面積の同じ三角形をつくることができる。
(面積はそのままで、三角形の形を変えられる)→等積変形
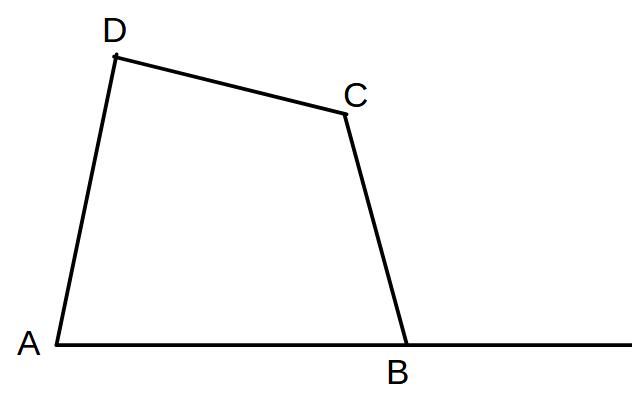
例2)
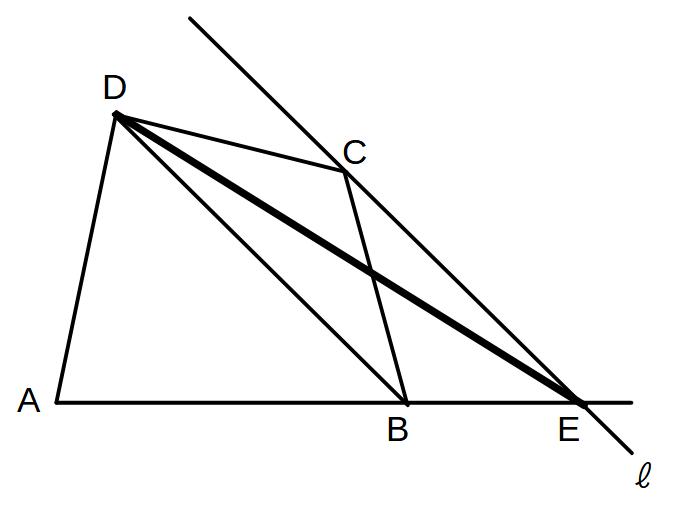
四角形ABCDにおいてABの延長線上に点を取って四角形ABCDと面積の等しい△ADEを作りたい
点Eをどこに取ればよいか。
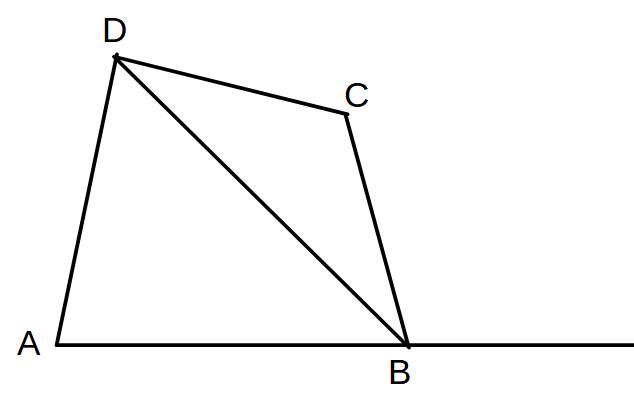
手順①
BDに線を引く→△BCDに注目
→△ABDは動かさず、△BCDを等積変形して△ADEをつくればよい。
手順②
点Cを取りBDに平行な直線ℓを引く
→BDを三角形の底辺として固定する
→ℓ上に頂点Eをとるかぎり△BCD=△BEDになるから面積は変わらない
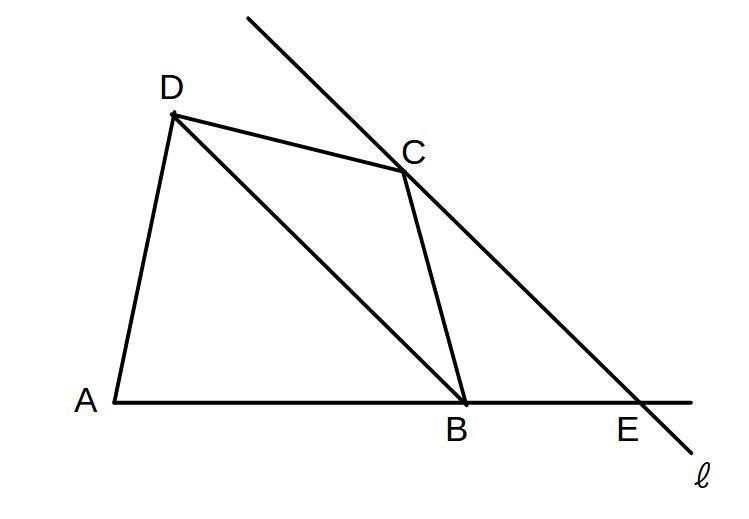
③ABの延長戦と直線ℓとの交点が、求める点となる
→△ABDはそのままで△BCD=△BEDに等積変形しているから、四角形ABCDと△ADEは面積が等しくなる